İstatistik derslerini tablet üzerinden çalışmanız şiddetle tavsiye olunur.
Hipotez Testi
Bu bölümde istatistikte hipotez testine ve hipotez testlerinin kullanımına değinilecektir.
İstatistikte hipotez, μ (ortalama), σ2 (varyans) gibi anakütle parametrelerine ilişkin ileri sürülen önermelerin olasılık kanunlarına göre geçerliliğini sınayan özel bir metoddur. Günümüzde konusu istatistik olsun ya da olmasın tüm akademik tezlerde sıkça kullanılan özel bir istatistik yöntemidir. İngilizce statistical hypothesis test (istatistiksel hipotez testi) olarak adlandırılır.
Hipotez testlerindeki genel maksat örneklemden elde edilen bilgiler ile anakütle parametrelerinin geçerliliğini sınamaktadır. Örneğin; "Bir fabrikada üretilen pillerin maksimum dayanma süresi 6 saattir. Fakat yapılan son testlerde bu sürenin 7 saat olduğu görülmüştür." dediğimizde aslında bir hipotez öne sürüyoruz. Diğer bir ifade ile pillerin dayanma sürelerinin 6 saatten farklı olduğunu iddia ediyoruz. İşte bu tür iddiaları istatistikte hipotez testleri ile sınamaktayız.
Konuya geçmeden önce hipotez testlerini tam olarak öğrenebilmek için istatistikte Merkezî Eğilim Ölçüleri, Dağılım Ölçüleri, Normal Dağılım ve Student t-Dağılımı konularının bilinmesi gerektiğini belirtirim. Eğer bu konularda bir eksikliğiniz varsa öncelikle ilgili konuları tekrar etmelisiniz.
Hipotez testleri birer parametrik testtir. Parametrik testler, verilerin normal dağılıma uyması durumunda kullanılan testlerdir.
Sıfır Hipotezi ve Alternatif Hipotez
Hipotez testlerinde sıfır ve alternatif olmak üzere iki farklı hipotez vardır:
Sıfır Hipotezi: Daha önce kabul görmüş ya da ispatlanmış hipotezdir. Bu hipotezi biz değiştiremeyiz. Zaten var olan hipotez budur. İngilizce null hypothesis (null hipotezi) [nal okunur] adlandırılır. Kimi kaynaklarda yokluk hipotezi adıyla belirtilir. Daima H0 ile gösterilir.
Alternatif Hipotez: Sıfır hipotezini çürütmek için öne sürülen hipotezdir. İngilizce alternative hypothesis olarak adlandırılır. Kimi kaynaklarda karşıt hipotez adıyla belirtilir. H1 ya da alternatif hipotezin kısaltması olan HA ile gösterilir.
Alternatif Hipotezin Üç Durumu
H1 olarak simgelediğimiz alternatif hipotezin üç durumu vardır. Tüm soruları bu üç durumdan birine göre belirleyip çözeceğiz.
Örneğin; "Yetişkin bir insanın uyku süresi 8 saattir." hipotezini ele alalım. Bu zaten var olan, kanıtlanmış bir hipotezdir. Bu yüzden bu hipotezi H0 olarak göstereceğiz. Şimdi H0 hipotezimize karşıt olan üç farklı hipotez öne sürelim:
Ortalamadan Yüksek Olma Durumu
H0 hipotezi ortalama uyku süresinin 8 saat olduğunu öne sürüyordu. Karşıt hipotezimiz H1'de ise bu sürenin 8'den fazla olduğunu öne sürüyoruz.
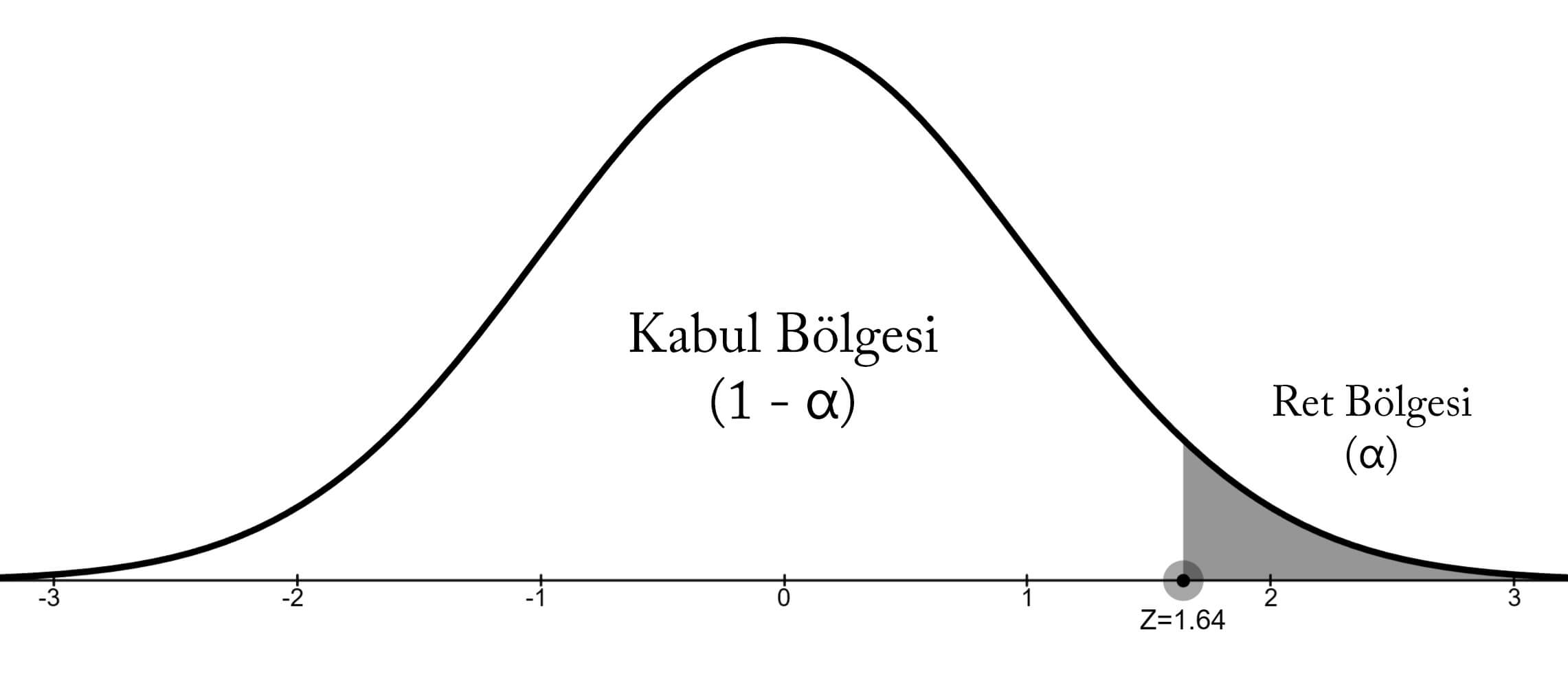
Bu durumda ret bölgesi standart normal dağılım grafiğinin sağ tarafında olacaktır. α (anlamlılık düzeyini) daima 0.05 (%5) alacağız. α ile belirtilen alan ret bölgesidir. Ret bölgesinden kasıt H0 hipotezinin ret edileceği bölgedir. Birazdan örneklerle açıklayacağız. Şimdilik kafanız karışmasın.
Ortalamadan Düşük Olma Durumu
H1 alternatif hipotezimiz ortalamanın 8 saatten az olduğu yönünde olacaktır.
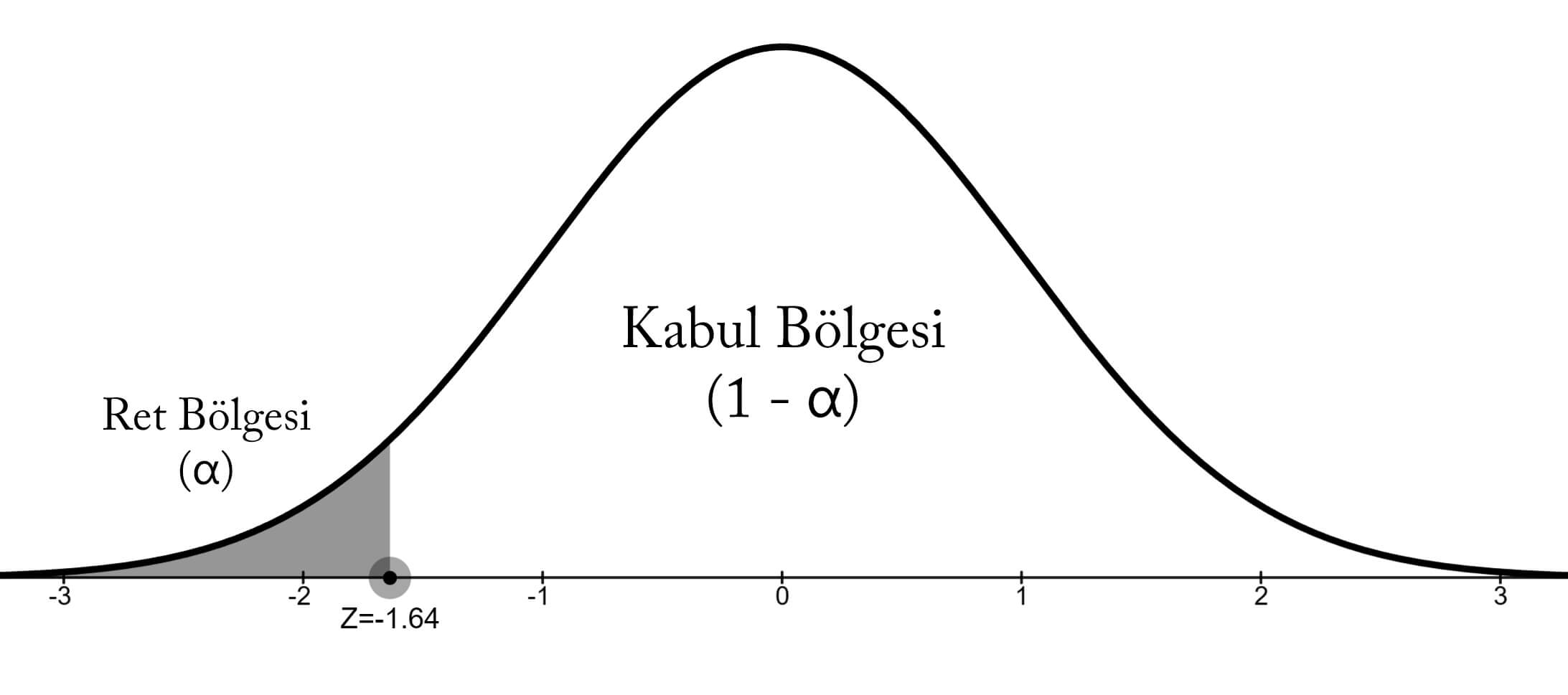
H0 sıfır hipotezi için ret bölgesi grafiğin sol tarafı olacaktır.
Ortalamadan Farklı Olma Durumu
H1 alternatif hipotezimiz ortalamanın 8 saatten farklı olduğu yönünde olacaktır.
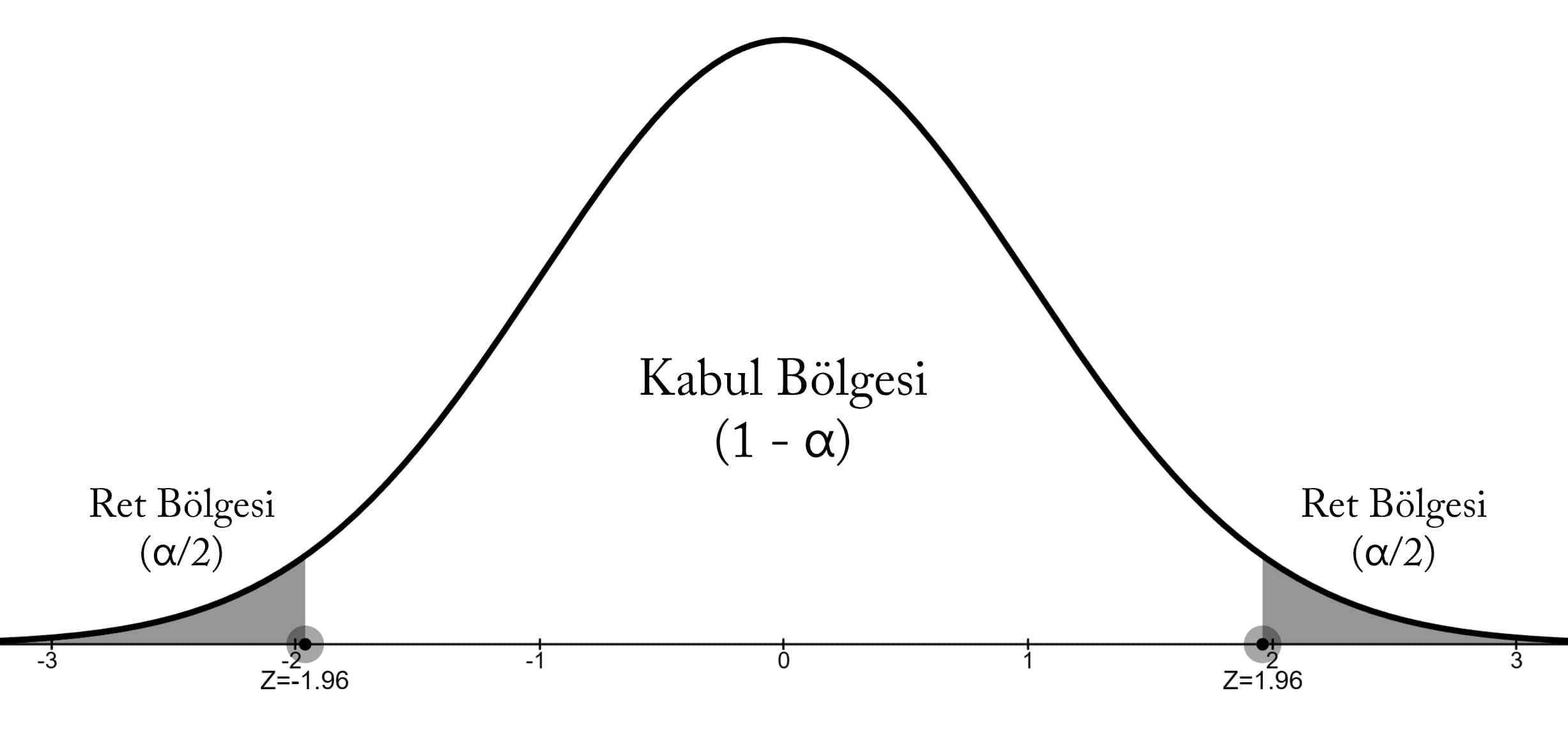
H0 sıfır hipotezi için ret bölgesi grafiğin sağ ve sol bölgelerindeki (α/2) alanları olacaktır.
Anlamlılık Düzeyi
Üstteki grafiklerde dikkat ettiyseniz ret bölgelerinin 1.64 ve 1.96 z değerlerine denk geldiğini görmüş olabilirsiniz. Peki bu değerler nereden gelmektedir?
Biz anlamlılık düzeyi α (alfayı) 0.05 (%5) belirlediğimizde aslında %95 güven düzeyinde deriz. Aynı şekilde 0.01 (%1) belirlediğimizde %99 güven düzeyinde demiş oluruz.
Normal dağılımda grafiğin sağ tarafı %50 olasılığa sahipken sol tarafı da %50 olasılığa sahiptir. α 0.05 belirlendiyse kabul bölgesinin olasılığı 0.50 - 0.05'den 0.45 (%45)'tir.
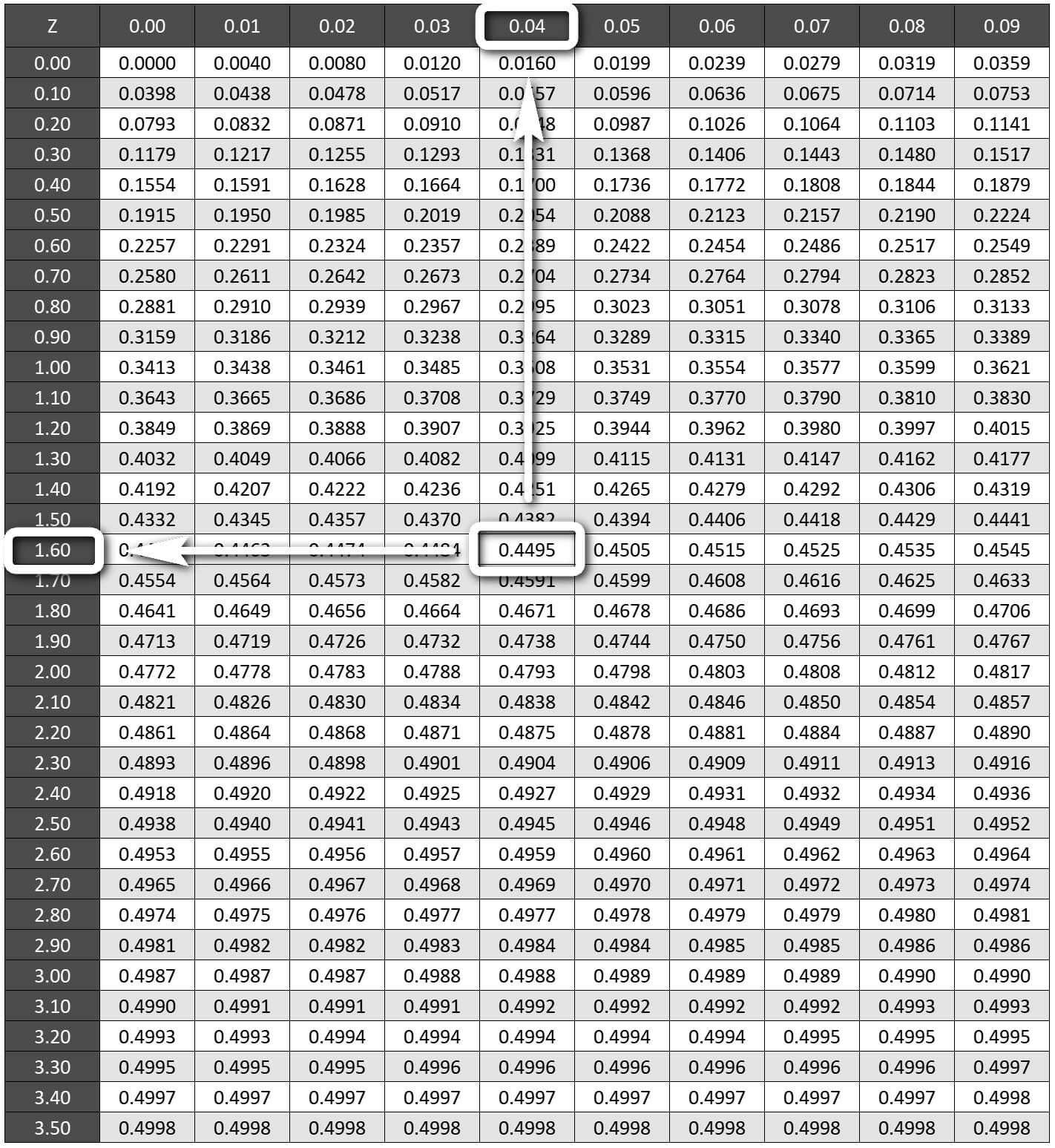
z-Tablosunda %45 olasılığa en yakın z değeri 1.64'tür. Diğer bir ifade ile α 0.05'in z değeri 1.64'tür. 1.64 değeri hipotez testlerinde kritik değer (critical value) olarak adlandırılır.
Çift taraflı hipotez testlerinde Anlamlılık düzeyi α 0.05 iken grafiğin bir yanı 0.05/2 = 0.025 alfa değerine sahipken diğer yanı da aynı alfa değerine sahip olacaktır. Grafiğin sol tarafındaki olasılık 0.50 - 0.025 = 0.4750 iken sağ tarafı da 0.4750 (%47.5) olasılığa sahiptir.
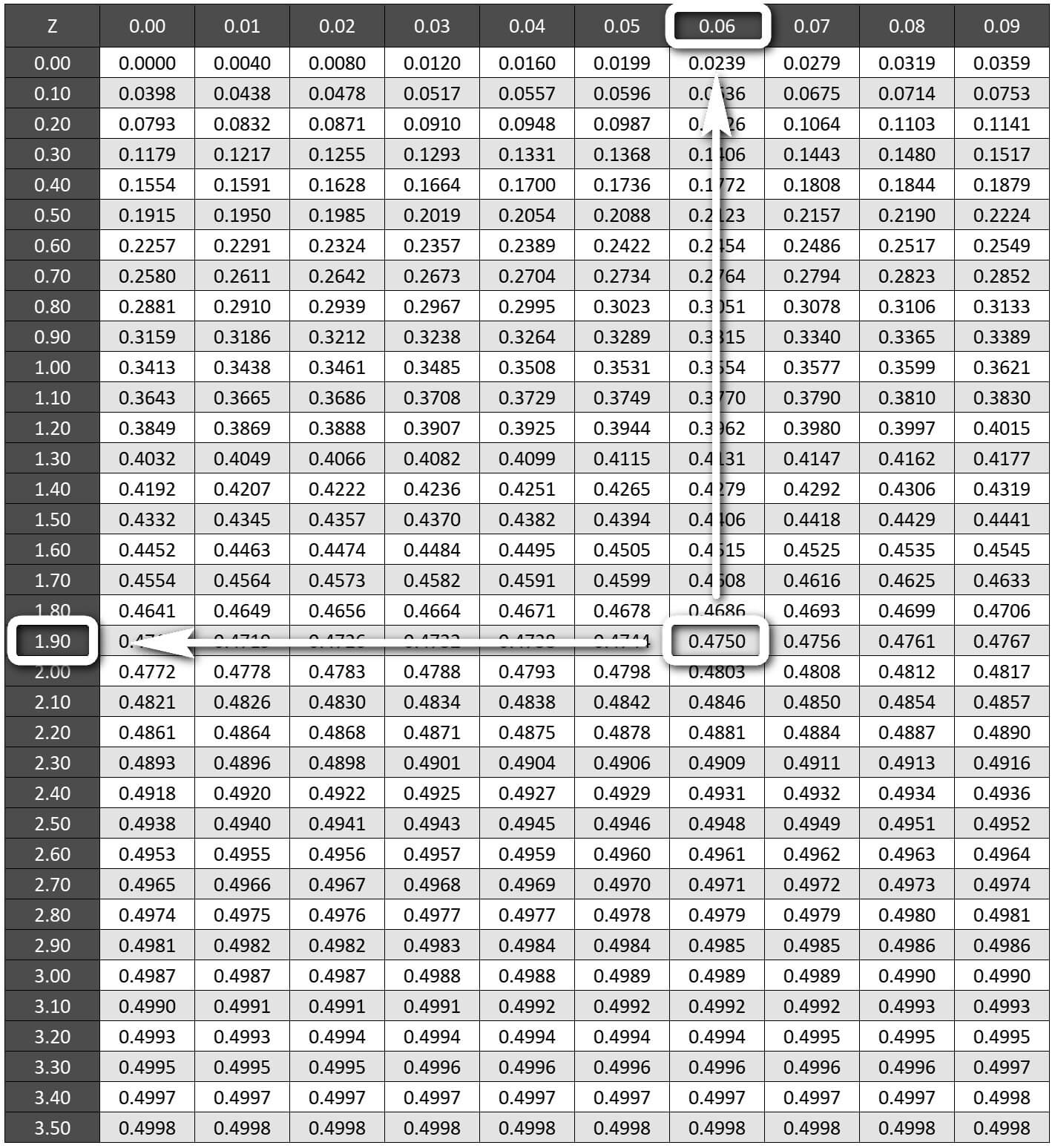
z-Tablosunda %47.50 olasılığının z değeri 1.96'dır. Diğer bir ifade ile α 0.025'in z değeri 1.96'dır. Çift taraflı testlerde kritik değer -1.96 ve 1.96 z değeridir.
α = 0.01 (%1) anlamlılık düzeyinde tek taraflı testlerde kritik değer 2.58 iken çift taraflı testlerde bu değer 2.33'tür.
Anakütle Varyansı Biliniyor ise Hipotez Testi
Anakütle varyansının (σ2) bilindiği durumda anakütle ortalaması için hipotez testi için öncelikle Zh (z-Skoru) olarak adlandırılan test istatistiğini (test statistic) hesaplamalıyız.
Zh test istatistiği (z-Skoru) bu formülle hesaplanır.



Örnek 1: Yapılan araştırmalarda yetişkin insanların ortalama uyku süresinin (μ) 8 saat ve standart sapmasının (σ) 1.2 saat olduğu görülmüştür. 100 kişilik bir örnek seçilmiş ve uyku süresinin ortalama 9.2 saat olduğu gözlemlenmiştir. Tüm yetişkin insanlar (anakütle) için ortalama uyku süresinin 8 saatten fazla olup olmadığını %95 güven düzeyinde test ediniz. N(0,1)
Soruda %95 güven düzeyi verildiği için α değeri 0.05 olacaktır. Aynı zamanda N(0,1) ifadesi verilerin normal dağılım sergilediğini belirtmektedir. Öncelikle hipotezimizi oluşturalım.
H0 sıfır hipotezi zaten kabul görmüş olan 8 saatlik ortalama uyku süresini belirtmektedir. H1 alternatif hipotemizde bu sürenin 8 saatten fazla olduğunu öne sürüyoruz. Şimdi test istatistiğimiz olan Zh'ı hesaplayalım.
z-Skorunu 10 bulduk.
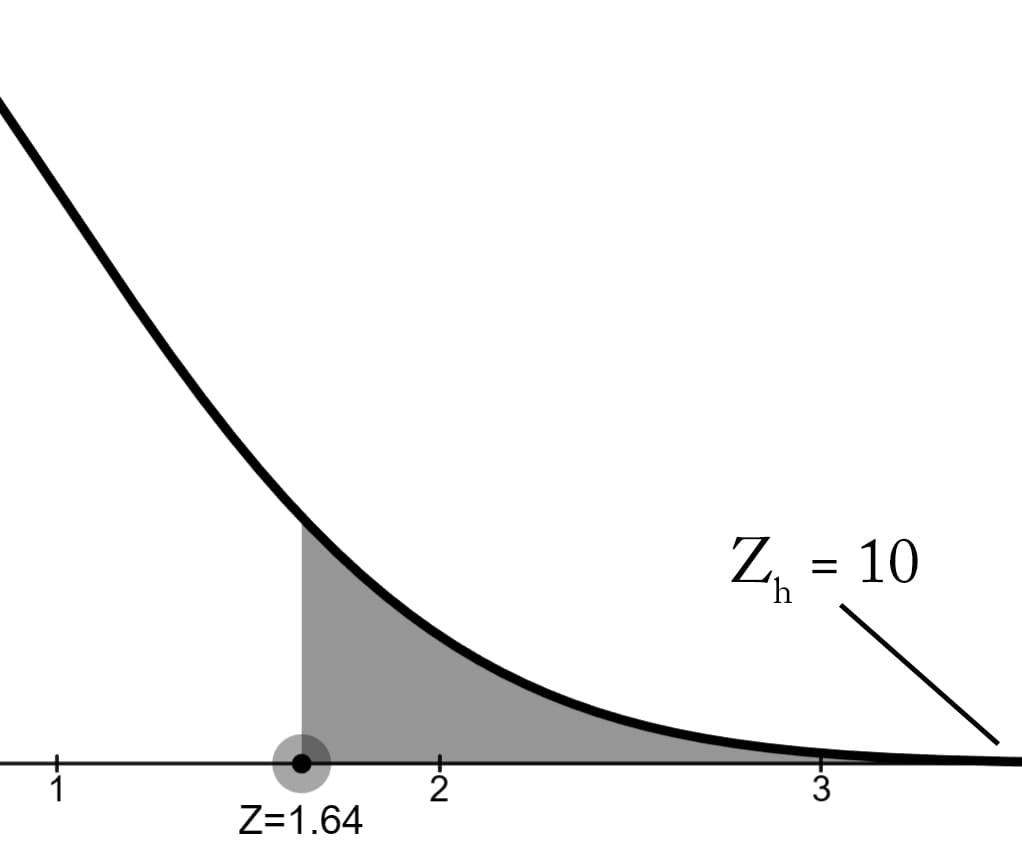
Zh > Z0.05 = 10 > 1.64 olduğu için H0 hipotezi ret edilir. H1 alternatif hipotez kabul edilir ve yetişkin insanlarda ortalama uyku süresi 8 saatten fazla olduğu sonucuna varılır.
Örnek 2: Bir fabrikada üretilen klavyelerin ortalama 5.2 yıl dayandığı gözlemlenmiştir. Standart sapma 1.9 yıldır. Bu fabrikadan seçilen son 240 üründe klavyelerin 4.8 yıl dayandığı gözlemlenmiştir. %95 güven düzeyinde ortalama klavye ömrünün 5.2 yıldan az olduğunu test ediniz. N(0,1)
Öncelikle hipotezimi oluşturuyoruz ve ortalama klavye ömrünün 5.2 yıldan az olduğunu H1 karşıt hipotezi ile öne sürüyoruz.
Test istatistiği Zh (z-Skoru) -3.26 bulunmuştur.
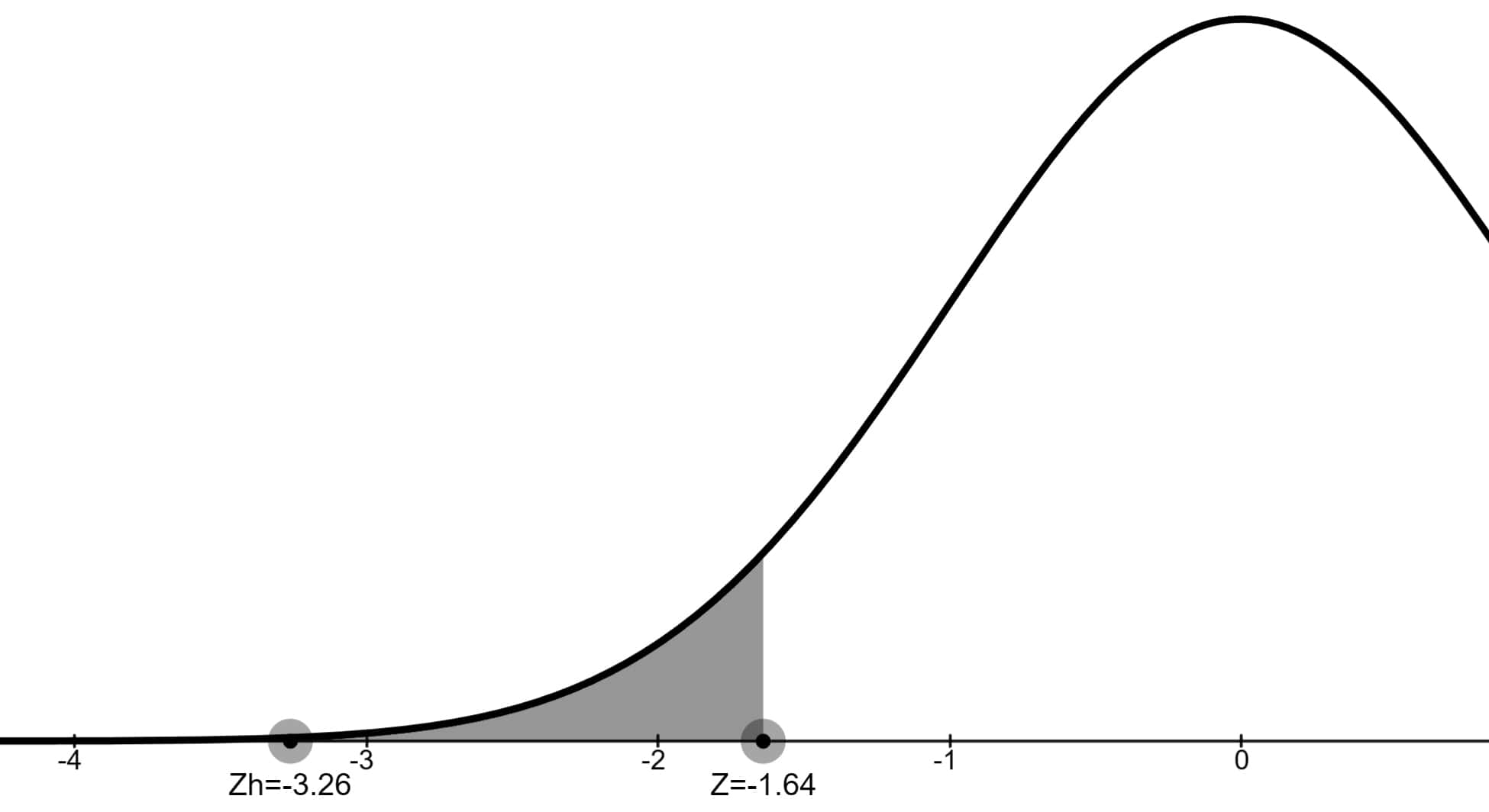
Zh değeri ret bölgesinde olduğu için H0 hipotezi ret edilir ve fabrikada üretilen klavyelerin ortalama 5.2 yıldan az dayandığını öne süren H1 alternatif hipotezi kabul edilir.
Örnek 3: Bir kasabada insanların aylık ortalama 10,000 TL harcadığı gözlemlenmiştir. Harcamaların standart sapması 4,600 TL'dir. Bu kasabadan rastgele seçilen 60 kişinin aylık ortalama harcamasının 10,500 TL olduğu hesaplandığına göre %95 güven düzeyinde ortalama aylık harcamanın tüm kasaba için farklı olup olmadığını test ediniz. N(0,1)
Soruda farklı olup olmadığı test edildiği için çift taraflı hipotez kullanmalıyız.
H1 hipotezimiz aylık ortalama harcamanın 10,000 TL'den farklı olup olmadığı yönünde olacaktır.
z-Skorunu 0.8420 bulduk.
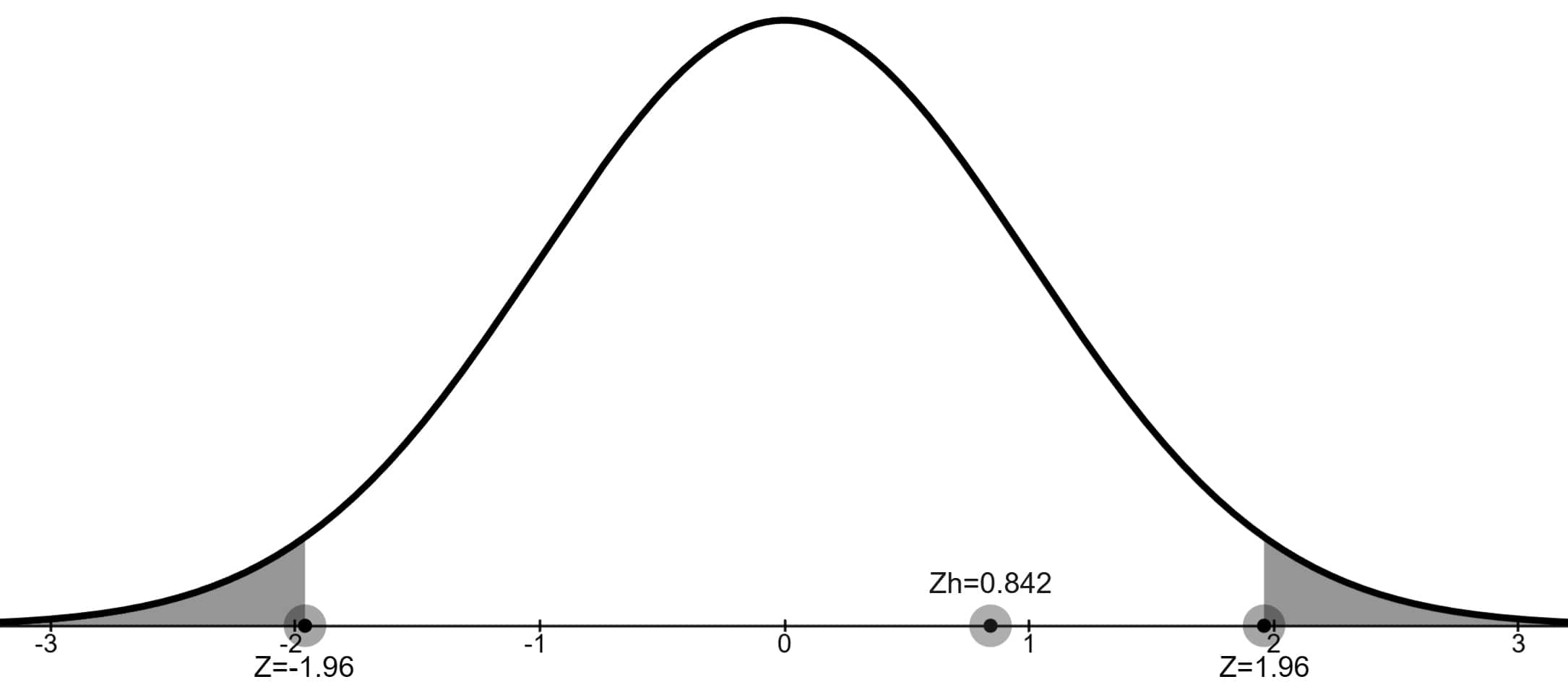
Zh test istatistiği kabul bölgesinde olduğu için H0 hipotezi reddedilmez ve tüm kasaba halkı için ortalama aylık harcamalarda fark olmadığı sonucuna varılır.
Anakütle Varyansı Bilinmiyor ise Hipotez Testi
Anakütle varyansının bilinmediği durumda anakütle standart sapması (σ) yerine örneklem standart sapmasını (s) kullanabiliriz.
Örneklem hacmi 30'dan fazla ise test istatistiği (z-Skoru)
Örneklem hacmi 30 ya da 30'dan az ise test istatistiği (t-Skoru)
olacaktır. Dikkat edilirse örneklem hacminin 30'dan fazla olduğu durumda z-Tablosu tercih edilirken 30 ya da 30'dan az olduğu durumda t-Tablosu yani Student t-Dağılımı tercih edilmektedir. Bu iki ayrıma özellikle dikkat etmeliyiz.
Örnek 4: Bir firmada çalışanların ağırlık ortalamasının 72.4 kg olduğu gözlemlenmiştir. Rastgele seçilen 80 kişinin ağırlık ortalaması 73.7 kg, standart sapması 4.5 kg bulunmuştur. %95 güven düzeyinde tüm çalışanlar için ağırlık ortalammasının 72.4 kg'dan fazla olup olmadığını test ediniz. N(0,1)
İlk olarak hipotezimizi oluşturalım.
Örneklem hacmi 30'dan fazla olduğu için z test istatistiğini (z-Skorunu) tercih edeceğiz.
z-Skorunu 2.58 bulduk.
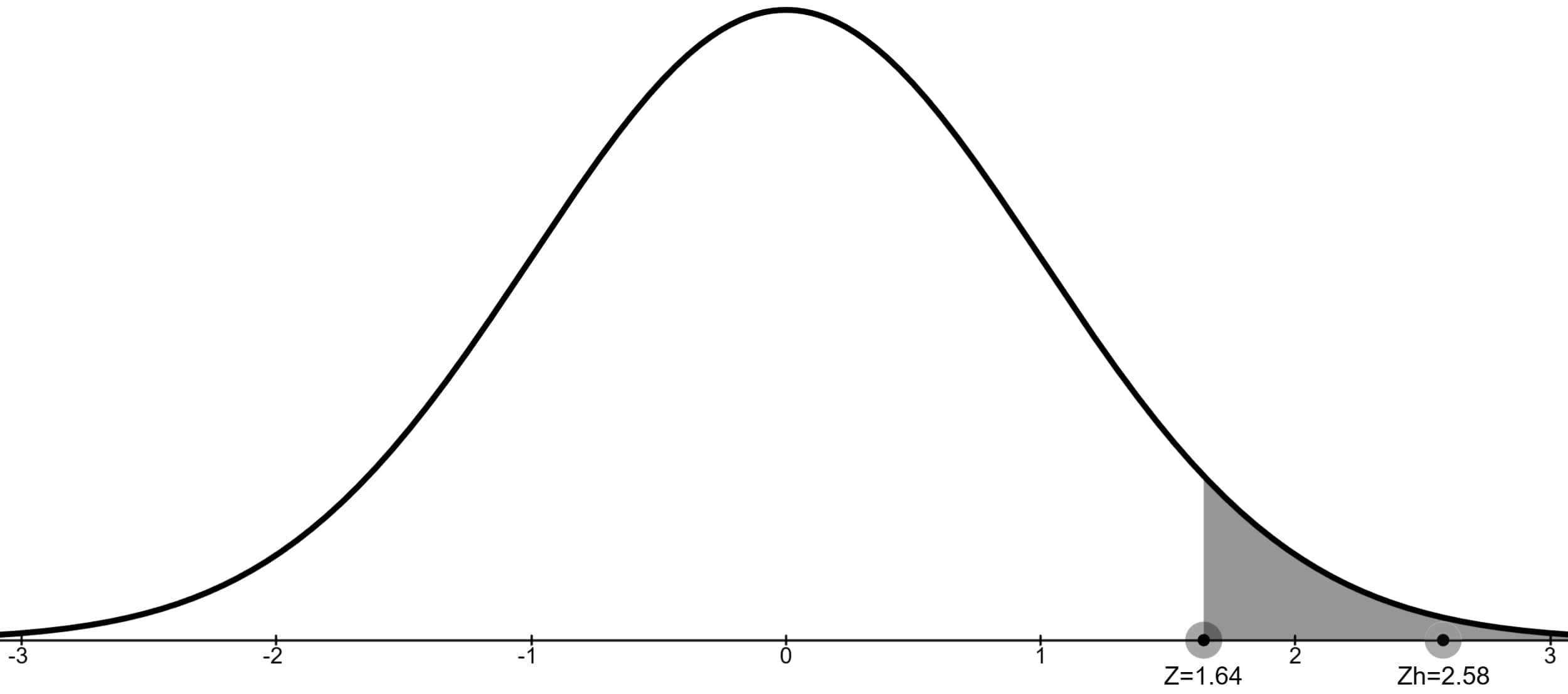
z test istatistiği ret bölgesinde olduğu için H0 hipotezi reddedilir ve tüm çalışanlar için ağırlık ortalamasının 72.4 kg'dan fazla olduğu sonucuna varılır.
Şimdi aynı soruyu Student t-Dağılımı ile çözelim.
Örnek 5: Bir firmada çalışanların ağırlık ortalamasının 72.4 kg olduğu gözlemlenmiştir. Rastgele seçilen 20 kişinin ağırlık ortalaması 73.7 kg, standart sapması 4.5 kg bulunmuştur. %95 güven düzeyinde tüm çalışanlar için ağırlık ortalammasının 72.4 kg'dan fazla olup olmadığını test ediniz. N(0,1)
Hipotezimiz değişmeyecektir.
Örneklem hacmi 30'dan az olduğu için t test istatistiğini (t-Skorunu) tercih edeceğiz.
t test istatistiğini (t-Skorunu) 1.26 bulduk.
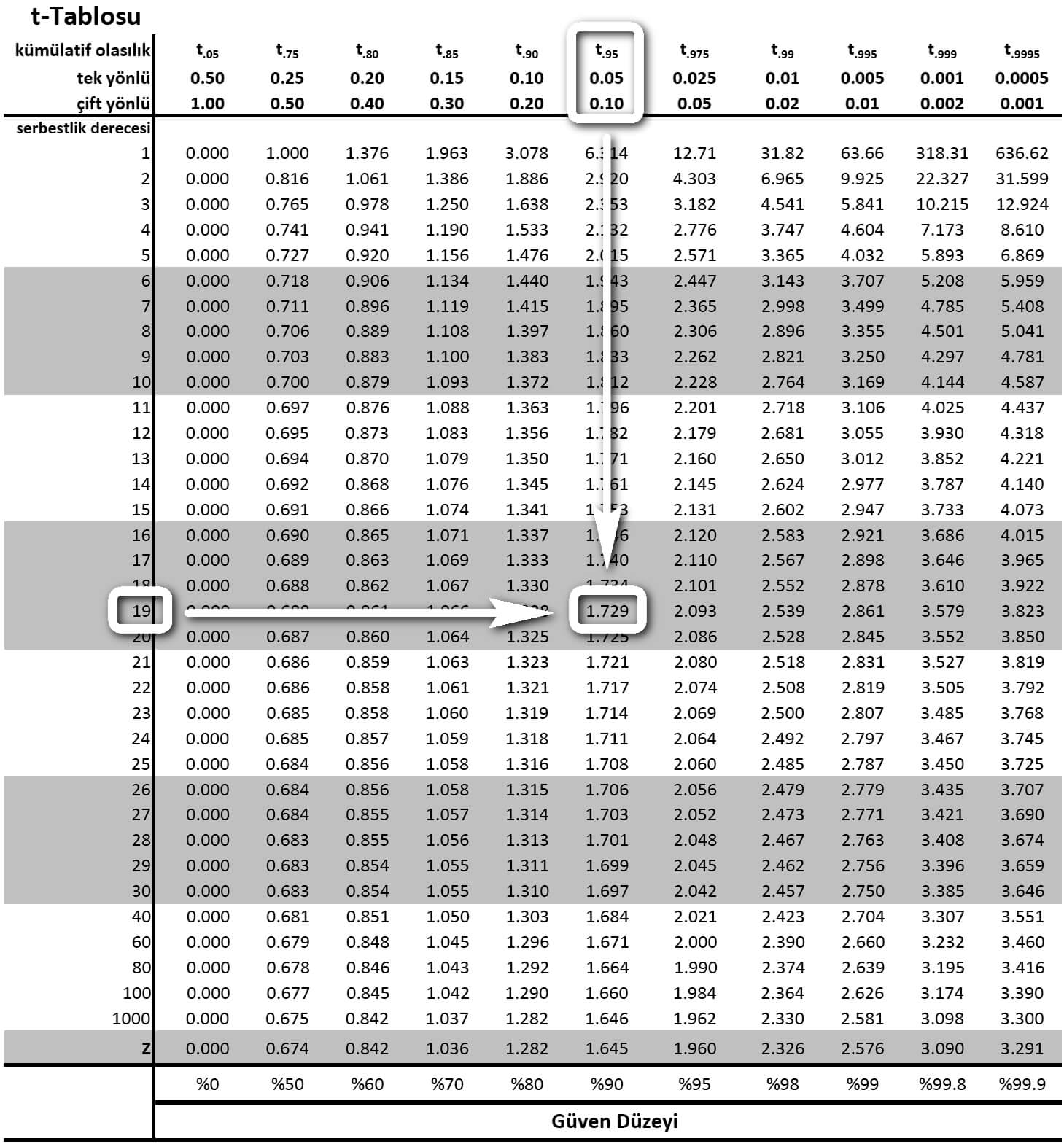
Hatırlanacağı üzere t-Tablosunda serbestlik derecesi v = n - 1 ile hesaplanır. 20 - 1'den serbestlik derecesi 19'dur. %5 anlamlılık düzeyinde bu alana karşılık gelen kritik değer 1.729'dur.
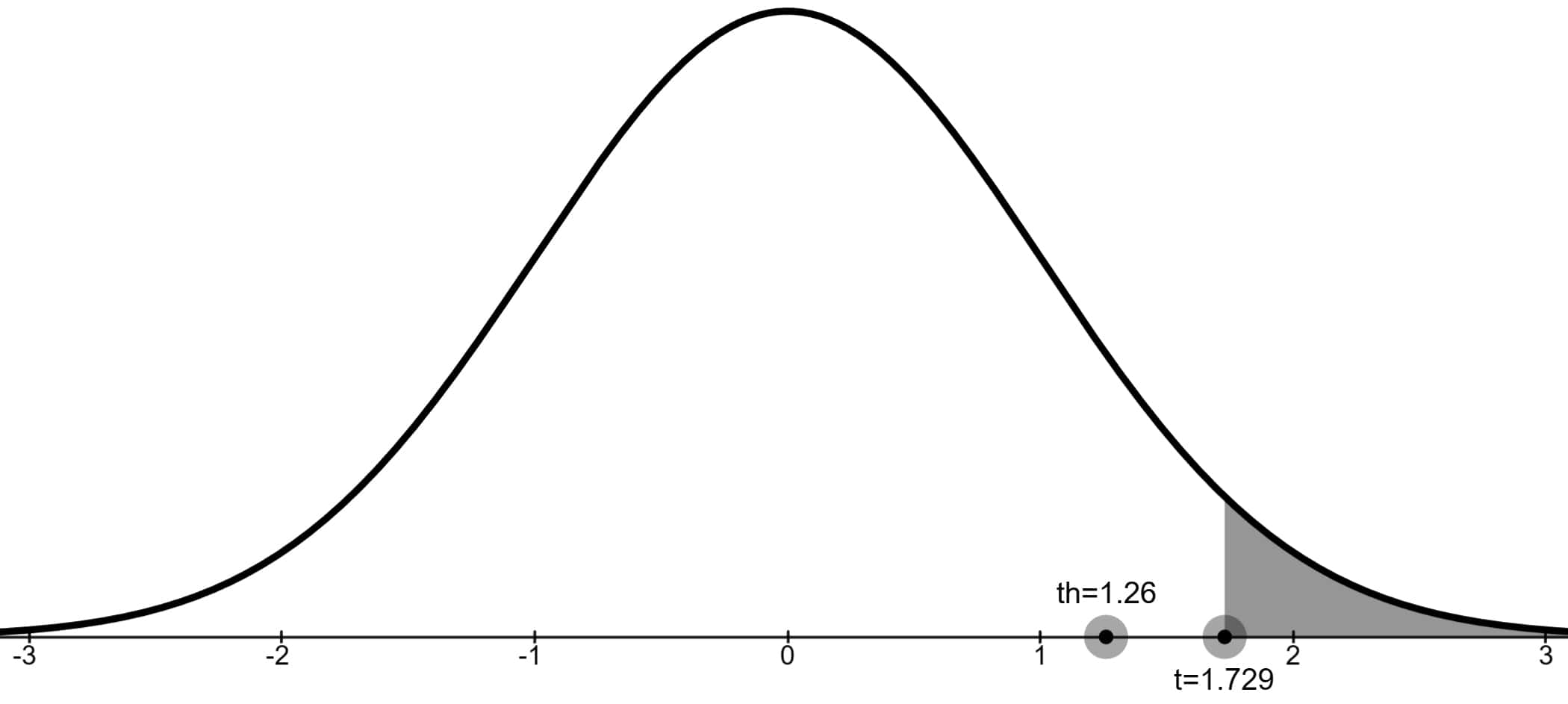
th < t0.05 = 1.26 < 1.729 olduğu için test istatistiği kabul bölgesindedir. H0 hipotezi reddedilmez ve tüm çalışanlar için ağırlık ortalamasının 72.4 kg'dan fazla olmadığı sonucuna varılır.
4. ve 5. örnekleri birlikte değerlendirecek olursak örneklem büyüklüğü arttıkça hipotezin daha doğru sonuç vereceği sonucuna ulaşabiliriz. 5. örnek olan bu örnekte muhtemelen II. Tip Hata ile karşı karşıyayız. Hata tiplerine birazdan değineceğiz.
Örnek 6: Bir fırındaki ekmeklerin ortalama 200 gram ağırlıkla üretildiği gözlemlenmiştir. Bu fırından rastgele alınan 24 ekmeğin ağırlık ortalaması 196 gram, standart sapması 8 gram bulunmuştur. %95 güven düzeyinde fırında üretilen tüm ekmeklerin ağırlık ortalamasının farklı olup olmadığını bulunuz. N(0,1)
Soruda anakütlenin ortalaması (μ) verilmesine rağmen varyansı (σ2) verilmemiştir. Aynı zamanda 30'dan az örnek seçilmiştir. Bu nedenle t-Dağılımı kullanmalıyız.
Alternatif hipotezimiz ekmeklerin ağırlık ortalamasının 200 gram olmadığı yönünde olacaktır. Bu nedenle çift yönünlü bir dağılım kullanacağız.
t-Skorunu -2.3979 bulduk.
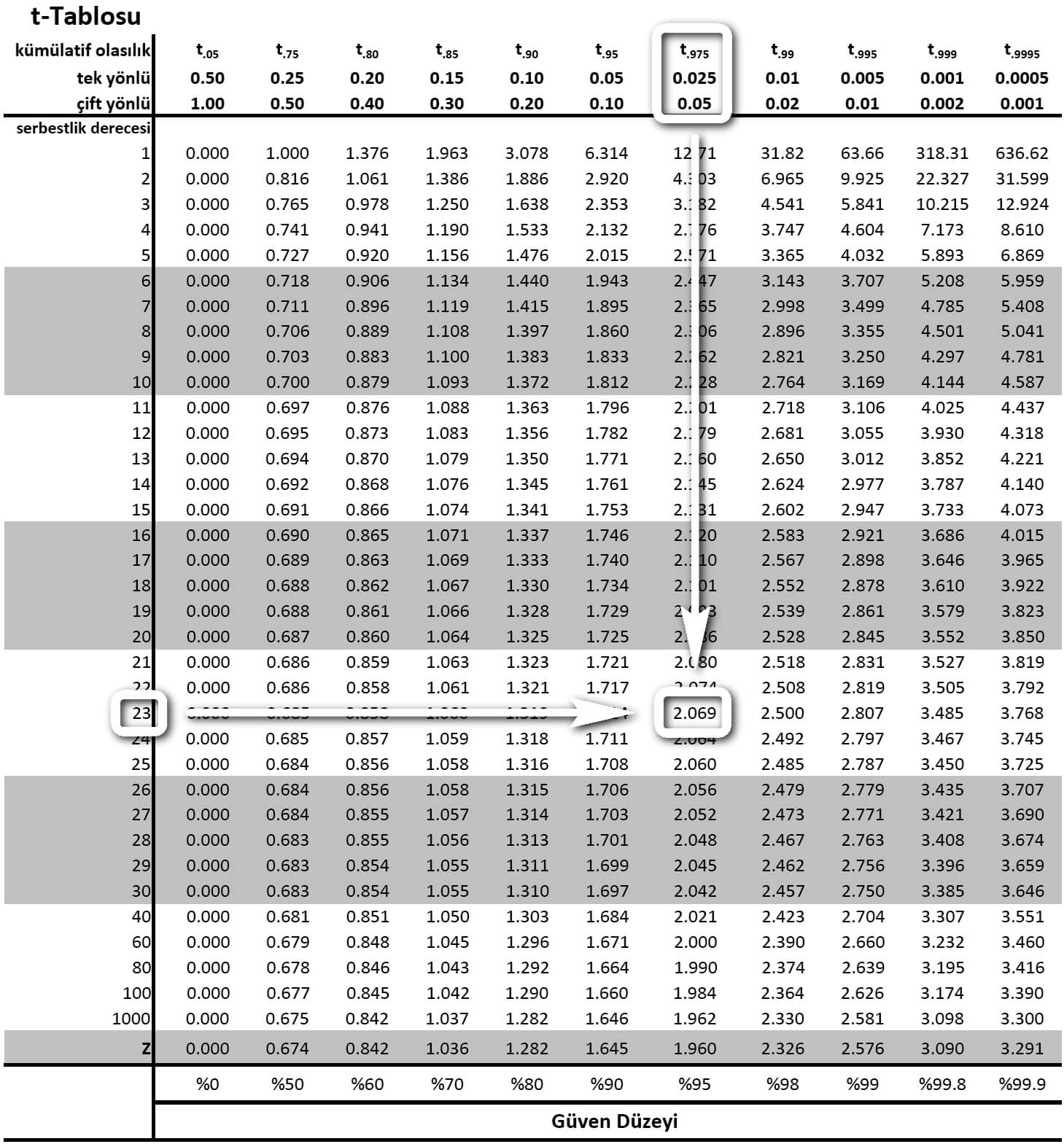
t tablosunda %5 anlamlılık düzeyinde serbestlik derecesi 23'e karşılık gelen kritik değer 2.069'dur.
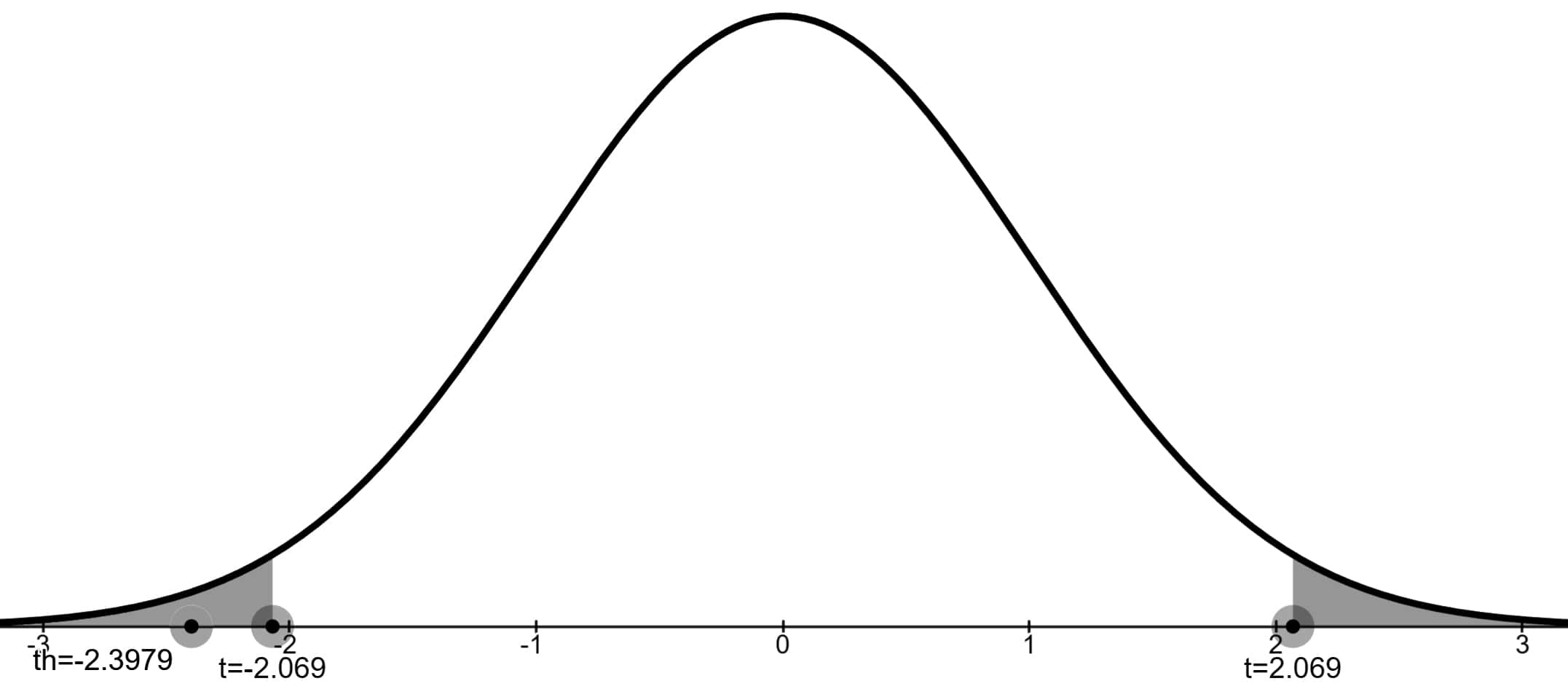
t-Skoru olan -2.3979 ret bölgesinde bulunduğu için H0 hipotezi reddedilir ve H1 hipotezi kabul edilir. Sonuç olarak bu fırında üretilen ekmeklerin ağırlık ortalamasının 200 gramdan farklı olduğu sonucuna varılır.
I. ve II. Tip Hata
Hipotez testinde 4 farklı sonuç ortaya çıkabilir:
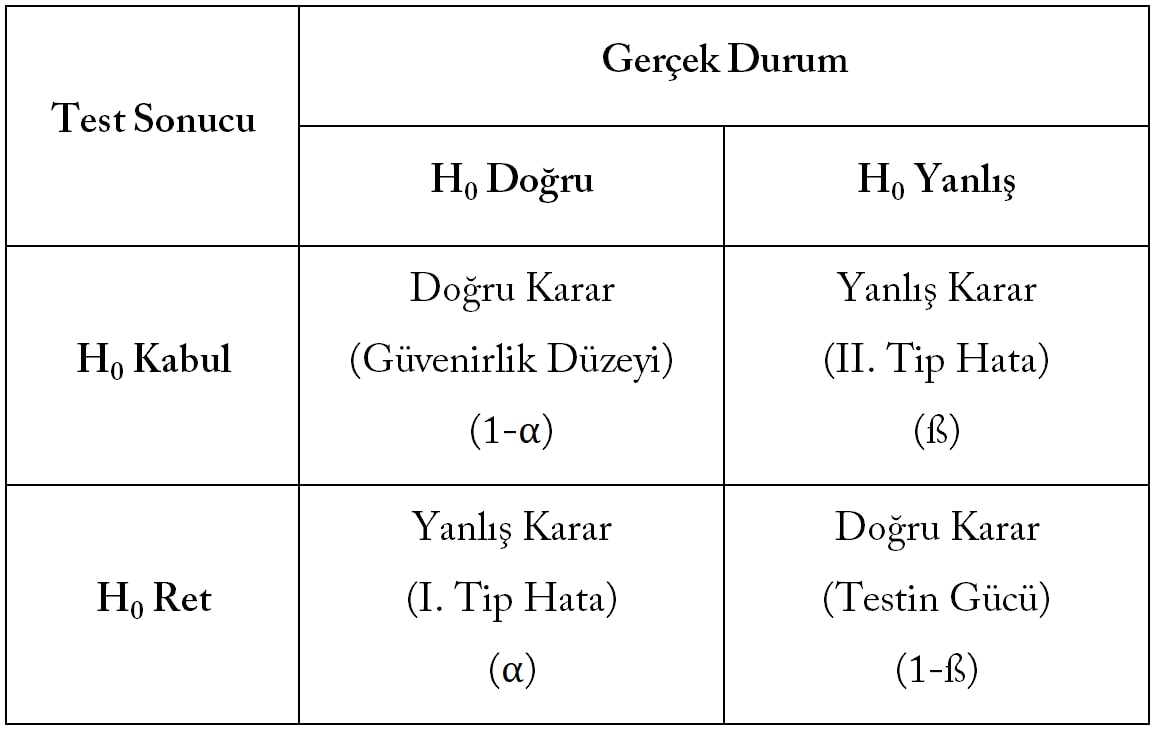
i. H0 hipotezi gerçekte doğrudur ve H0 kabul edilmiştir. (Güvenirlik Düzeyi)
ii. H0 hipotezi gerçekte yanlıştır ve H0 kabul edilmiştir. (II. Tip Hata)
iii. H0 hipotezi gerçekte doğrudur ve H0 reddedilmiştir. (I. Tip Hata)
iv. H0 hipotezi gerçekte yanlıştır ve H0 reddedilmiştir. (Testin Gücü)
α: Gerçekte doğru olan H0 hipotezinin reddedilme olasılığı
β: Gerçekte yanlış olan H0 hipotezinin kabul edilme olasılığı
1-α: Gerçekte doğru olan H0 hipotezinin kabul edilme olasılığı (Güvenirlik Düzeyi)
1-β: Gerçekte yanlış olan H0 hipotezinin reddedilme olasılığı (Testin Gücü)
Hipotez testleri %100 güvenilir testler değildir. I. Tip Hataya en büyük sebep örneklemin az sayıdaki veri biriminden oluşturulması ya da yanlış seçilmesidir. Örneğin; boy uzunluklarının ortalaması hakkında bir hipotez testi kurduğumuzda örneklem hacmini boyu fazla olanlar ile oluşturduğumuzda I. Tip Hata ile karşılacağız. H0 gerçekte doğru olmasına rağmen ret edeceğiz. II. Tip Hataya en büyük sebep ise anakütle parametrelerinin yanlış ölçülmesidir. Örneğin; bir kasabadaki ortalama tüketim harcamalarının tespitinde standart sapma yanlış hesaplandığında H0 gerçekte yanlış olmasına rağmen hipotez testimizde kabul etme durumu söz konusu olabilecektir.
I. Tip Hatayı "Güvenirlik Düzeyi" ile önleyebilirken II. Tip Hatayı "Testin Gücü" ile önleyebiliriz.
SPSS'te Hipotez Testi
SPSS'te hipotez testi yapmak oldukça basittir.1
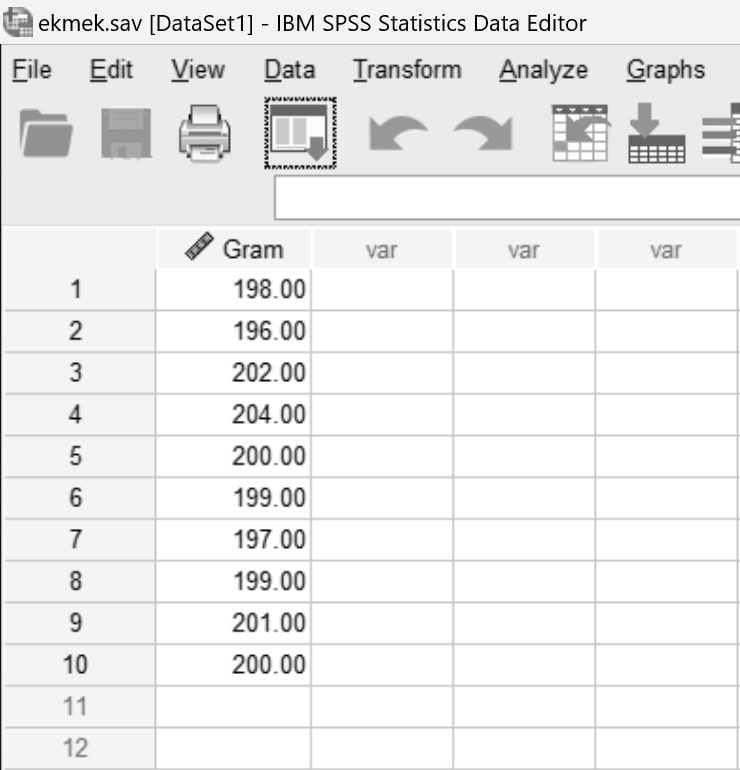
Bir fırındaki ekmeklerin ortalama ağırlığı 200 gram olsun. Bu fırından 10 ekmekten oluşan bir örnek seçelim. Her bir ekmeğin ağırlığı görseldeki gibidir. Amacımız fırında üretilen ekmeklerin ortalama ağırlıklarının 200 gramdan farklı olup olmadığını test etmek.
Dilerseniz bu veri setinin SPSS dosyasını yukarıdaki bağlantıdan indirebilirsiniz.
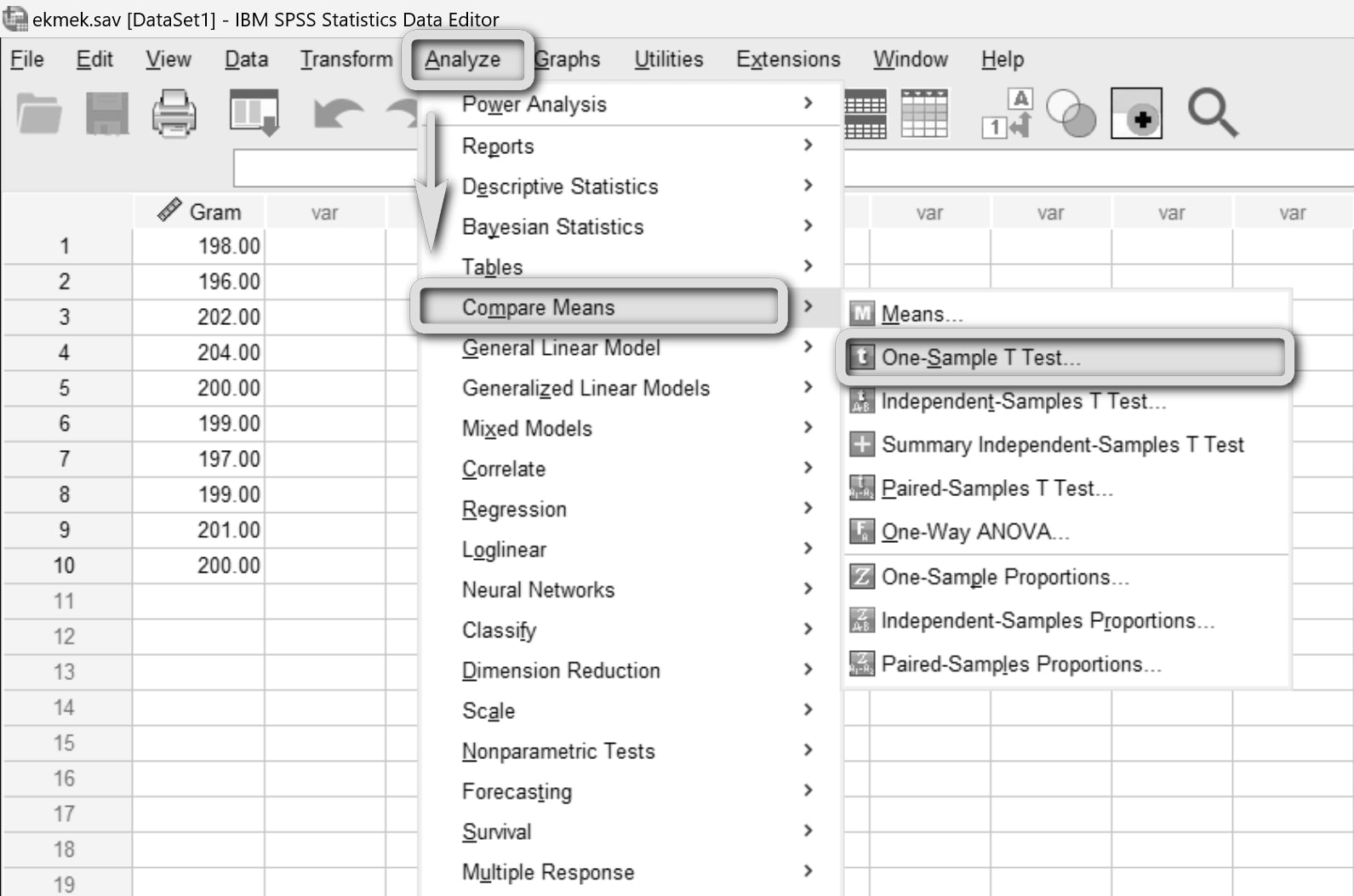
Menüden Analyze > Compare Means > One-Sample T Test... yolunu izliyoruz.
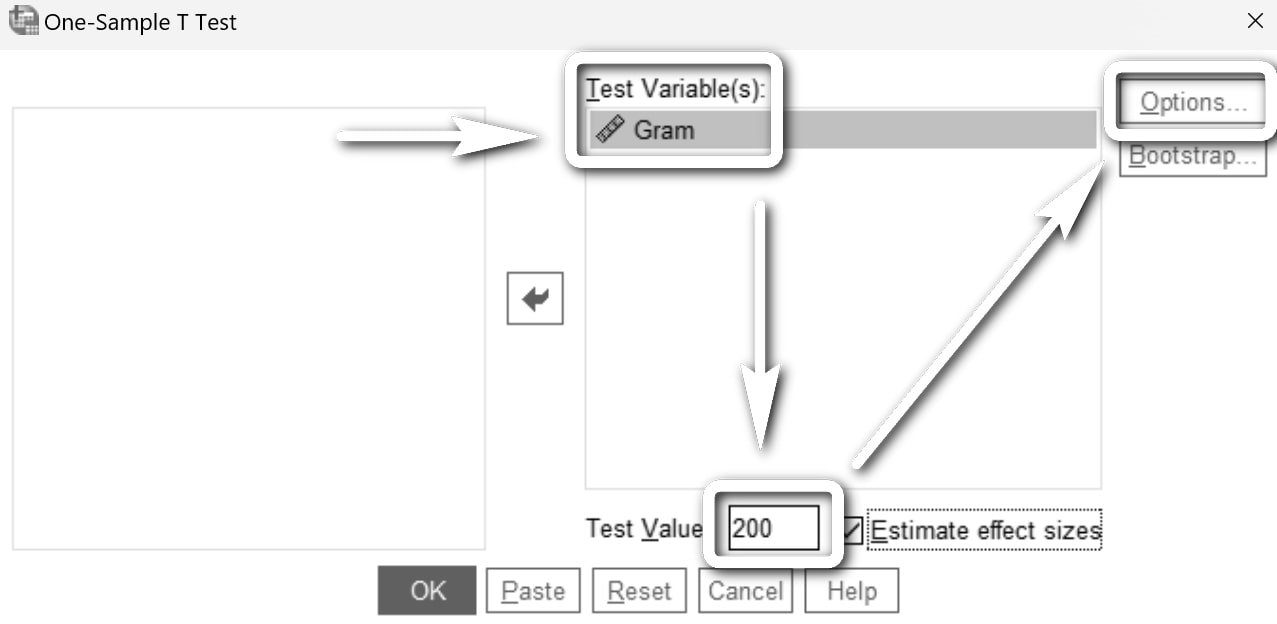
Gram değişkenini Test Variable(s) alanına yerleştiriyoruz. Test Value test değerini 200 yapıyoruz ve Options...'a tıklıyoruz.
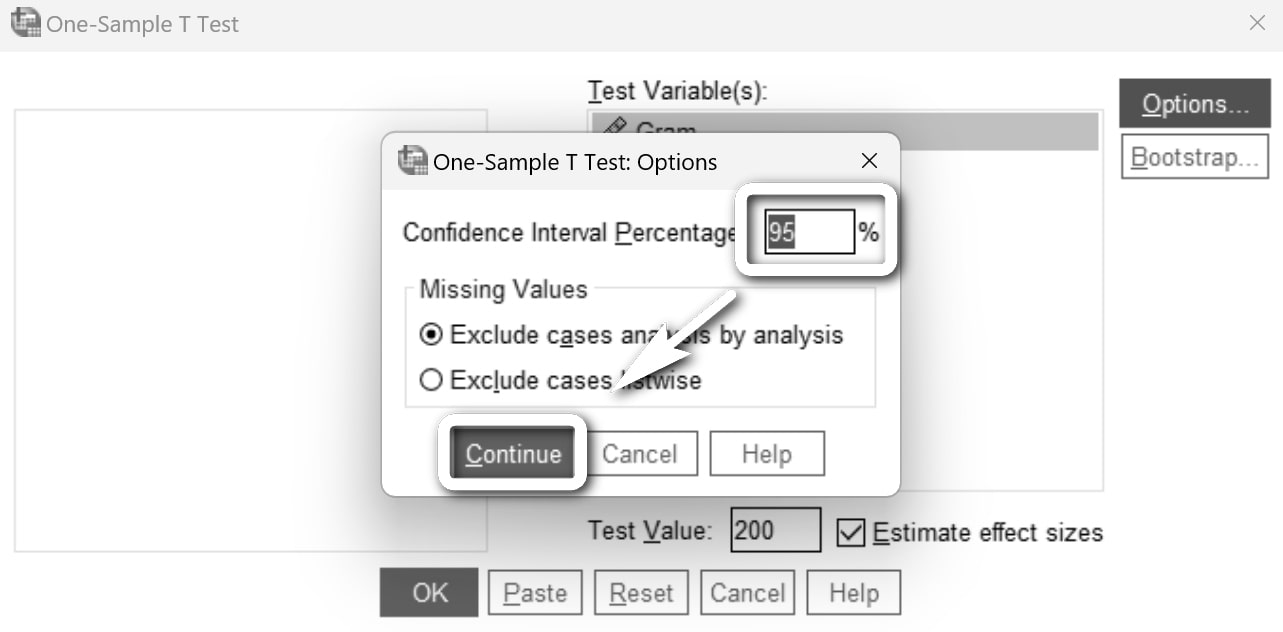
Güven düzeyinin %95 olduğuna emin olduktan sonra Continue'ya tıklıyoruz.
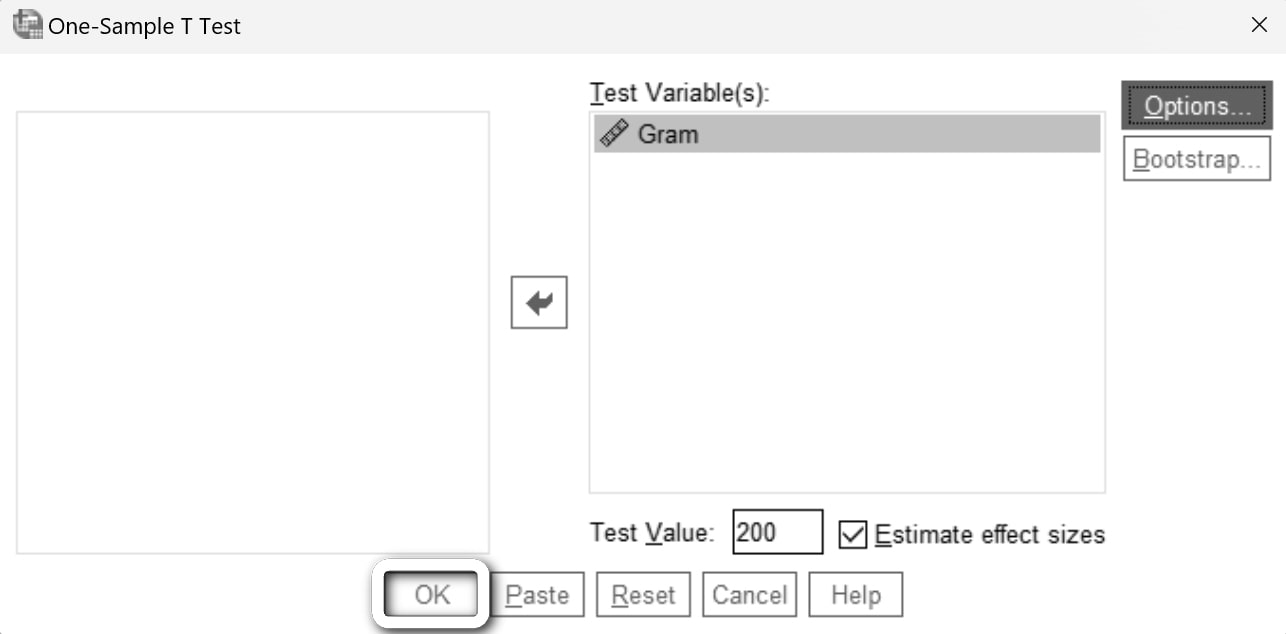
Artık tek yapmamız gereken OK düğmesine tıklamak.
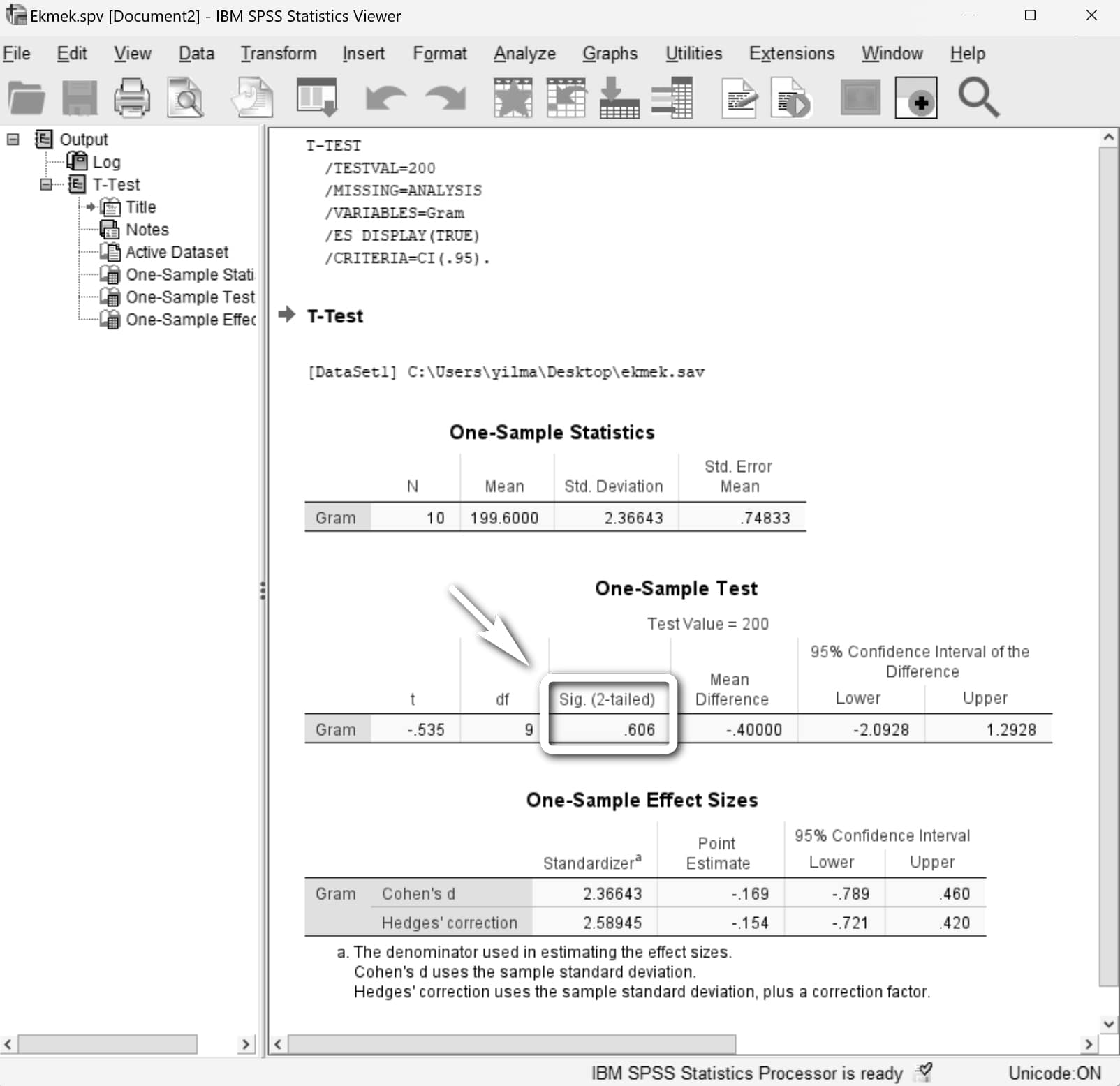
Output (çıktı) penceresi açılacaktır. Tüm bu tablolarda bizim için önemli olan Sig. (2-tailed) olarak belirtilen "Çift Taraflı Önemlilik Değeri"dir. Bu değer 0.606 çıkmıştır. p-value (p-değeri) olarak da adlandırılan significance value (anlamlılık değeri) 0.05'ten büyük olduğu için H0 hipotezi kabul edilir. Yani fırında üretilen ekmeklerin ortalama ağırlıkları 200 grama eşittir.
SPSS'te Sig. (Significance Value) değerini şu şekilde yorumlarız:
- Sig. Değeri < 0.05 ise H0 hipotezi reddedilir ve H1 hipotezi kabul edilir.
- Sig. Değeri > 0.05 ise H0 hipotezi kabul edilir ve H1 hipotezi reddedilir.
Python'da Hipotez Testi
Python ile de hipotez testi yapabiliriz. Bunun için scipy kütüphanesini kullanmalıyız.
Örnek 6'da yaptığımız hipotez testini Python ile kuralım ve hipotezi test edelim:
Bir fırındaki ekmeklerin ortalama 200 gram ağırlıkla üretildiği gözlemlenmiştir. Bu fırından rastgele alınan 24 ekmeğin ağırlık ortalaması 196 gram, standart sapması 8 gram bulunmuştur. %95 güven düzeyinde fırında üretilen tüm ekmeklerin ağırlık ortalamasının farklı olup olmadığını bulunuz. N(0,1)
Kodları çalıştırdığımızda
t skoru: -2.449489742783178
p-değeri: 0.02234065938289924
Sıfır hipotezi reddedildi: Fırında üretilen
tüm ekmeklerin ağırlığı 200 gramdan farklıdır.
sonucu yazdırılacaktır.
Sıra Sizde
Uygulama: Bir fabrikada üretilen tüm ürünlerin ortalama uzunluğunun 40.34 cm olduğu bilinmektedir. Bu fabrikadan seçilen 120 ürünün ortalama uzunluğunun 42.44 cm, standart sapmasının 8.17 cm olduğu ölçülmüştür. %95 güven düzeyinde tüm ürünlerin ortalama uzunluğunun 40.34 cm'den fazla olup olmadığını test ediniz. N(0,1)
Soruda anakütlenin standart sapması verilmemiştir. Buna rağmen örneklem 120 veri biriminden oluşmaktadır. Bu nedenle z-Dağılımına yönelik hipotez testi yapacağız.
Alternatif hipotezimiz ortalama ürün ağırlıklarının 40.34 cm'den fazla olduğu yönünde olacaktır.
z-Skorunu (test istatistiğini) 2.8157 bulduk.
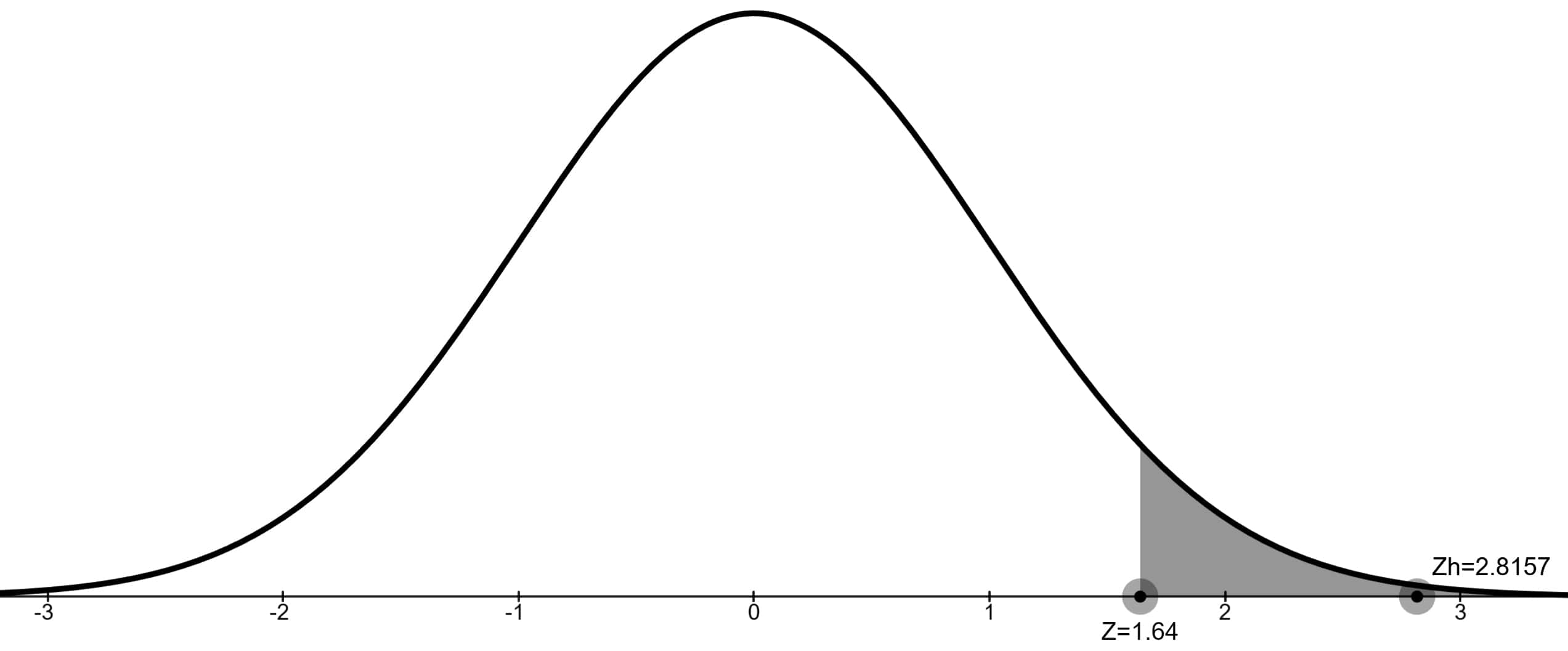
Test istatistiği ret bölgesinde olduğu için H0 hipotezini reddederiz. Tüm ürünlerin ortalama uzunluğu 40.34 cm'den fazladır.
Uygulama: Bir okulda matematik sınav notlarının tüm yıllar boyunca ortalama 74 olduğu kaydedilmiştir. 18 öğrenci yapılan son matemetik sınavında ortalama 64 almıştır. Bu öğrencilerin sınav notlarının standart sapması 17'dir. %95 güven düzeyinde tüm öğrencilerin sınav notu ortalamalarının 74'ten farklı olup olmadığını test ediniz. N(0,1)
Bu soruda da anakütlenin standart sapması verilmemiştir. Örneklem 18 öğrenciden oluşmaktadır. Bu nedenle t-Dağılımına yönelik hipotez testi yapacağız. Farklı olup olmadığı sorulduğu için de çift yönlü bir dağılım tercih etmeliyiz.
Alternatif hipotezimiz not ortalamasının 74'ten farklı olup olmadığı yönünde olacaktır.
t-Skorunu (test istatistiğini) 2.4254 bulduk.
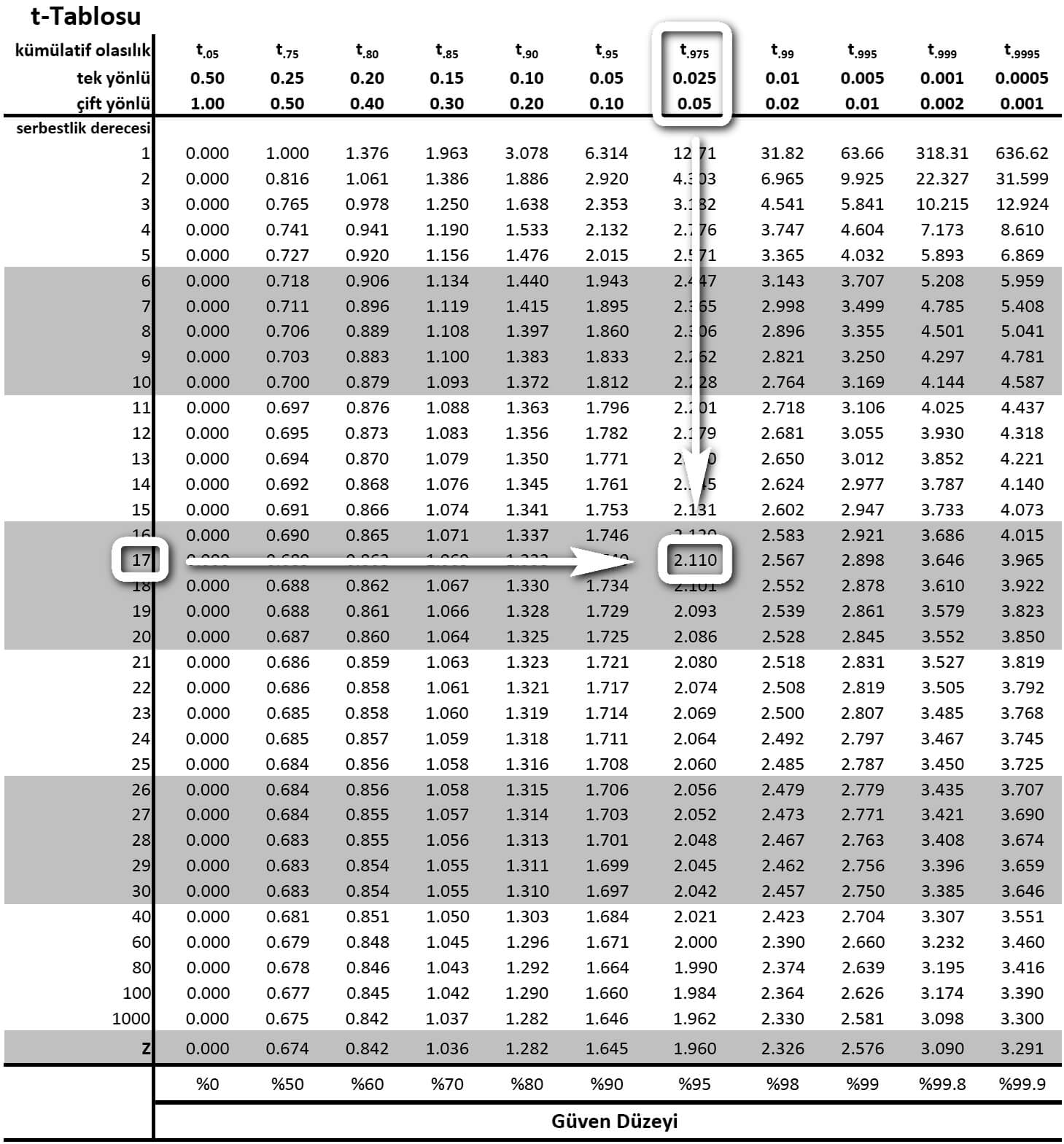
t-Tablosunda 17 serbestlik derecesinde çift taraflı 0.05 α değerine denk gelen kritik değer 2.110'dur.
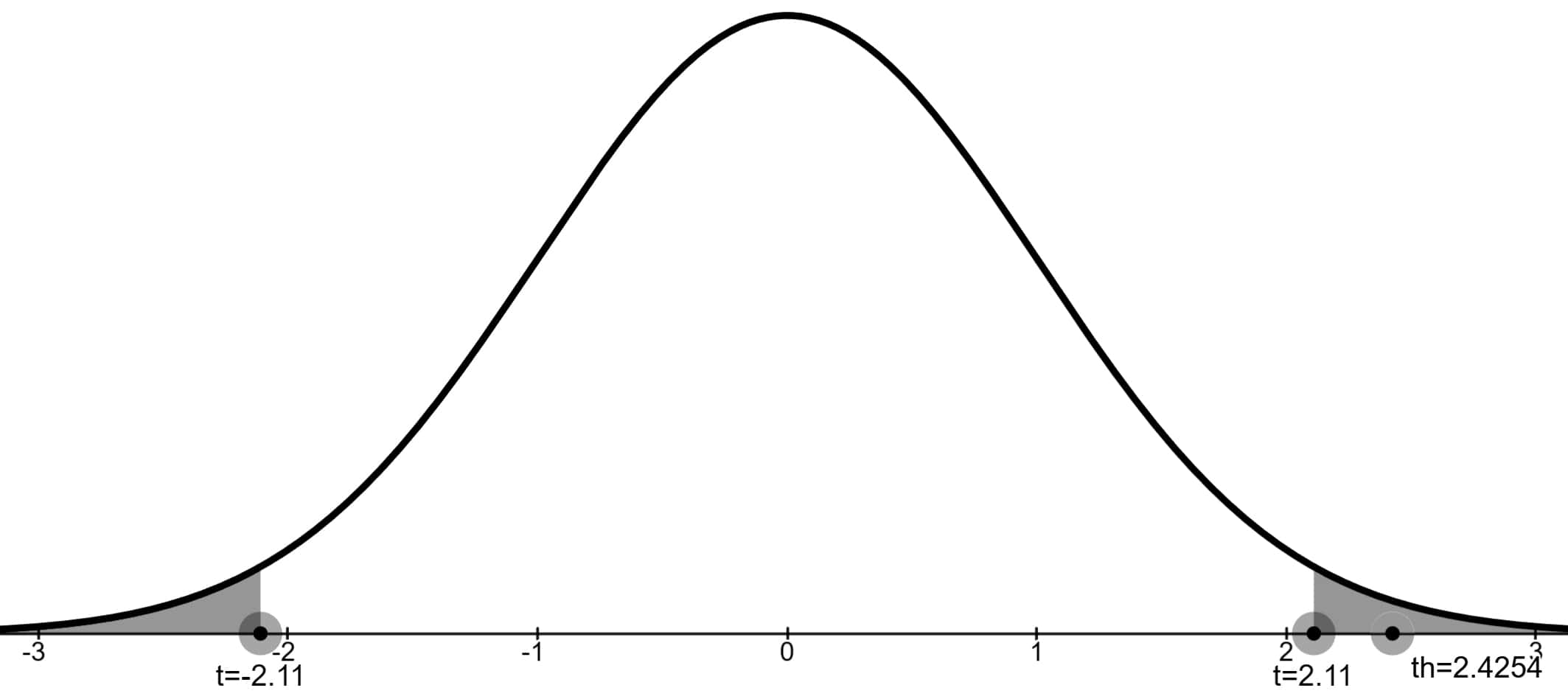
Test istatistiği ret bölgesinde olduğu için H0 hipotezi reddedilir. Okuldaki tüm öğrenciler için sınav notlarının ortalaması 74'ten farklıdır.
H0 hipotezini reddetmemize rağmen sonucun I. Tip Hata olabileceği de göz önünde bulundurulmalıdır.