İstatistik derslerini tablet üzerinden çalışmanız şiddetle tavsiye olunur.

Güven Aralığı ve Student t-Dağılımı

Bu bölümde istatistikte güven aralığı ve Student t-Dağılımı kavramlarına değinilecektir.

Güven Aralığı

z-Dağılımı için Güven Aralığı

Student t-Dağılımı

t-Dağılımı için Güven Aralığı

SPSS'te Güven Aralığı

Python'da Güven Aralığı

Güven Aralığı

İstatistikte anakütle parametrelerine (anakütle ortalamasına ve standart sapmasına) ulaşmak çoğu zaman uzun, yorucu, zahmetli ve maliyetli olmaktadır. Bu nedenle bir önceki bölüm olan Örnekleme Teorisi'nde anlatılan örnekleme yöntemlerinden biri tercih edilir ve örneklem oluşturulur. Oluşturulan örneklem ile anakütlenin parametreleri tahmin edilmeye çalışılır.

Örneklem istatistiği ile anakütle parametrelerinin tahmin edilmesine istatistiksel tahmin denir. Bu tahmin

Nokta Tahmin
Aralıklı Tahmin

olmak üzere iki farklı şekilde yapılabilir. Tahminlerde anakütle parametresi θ (teta) işareti ile gösterilirken, örneklem istatistiği \( \hat{\theta} \) (teta üzeri şapka) işareti ile gösterilir.

İstatistikte şapka işareti daima tahmin değerlerini gösterir. Bu nedenle \( \hat{\theta} \) anakütleyi tahmin etmek için kullanılan bir istatistik işaretidir.

Nokta tahmininde anakütle parametreleri olan ortalama (μ) ve standart sapma (σ) nokta atışı bir tahmin ile bulunur. Örneğin; örneklem ortalaması ile anakütle ortalamasının 44.8 olduğunu söylemek bir nokta tahminidir. Fakat nokta tahminleri güvenilir değildir. Bu nedenle aralıklı tahmin kullanılır. "Anakütle ortalaması %95 olasılıkla 40.6 ile 48.2 arasındadır." şeklinde bir çıkarsamada bulunulabilir. İşte bu tür çıkarsamalarda bulunabilmek için aralıklı tahmininin en popüler yöntemi olan güven aralığı (confidence interval) adı verilen bir tekniği kullanmamız gereklidir.

z-Dağılımı için Güven Aralığı

Normal Dağılım bölümünü anladıysanız z-Dağılımı aslında bir standart normal dağılımdır. z-Dağılımı (Standart Normal Dağılım) örneklemdeki birim sayısının 30'dan büyük olması durumunda kullanılır. Diğer bir ifade ile n > 30 koşulu aynı zamanda z-Dağılımının da koşuludur.

Güven aralığında 1 - α (alfa) ile gösterilen güven düzeyi (olasılık düzeyi) kullanılır. "%95 olasılıkla", "%95 güven düzeyi ile" ya da "%5 hata ile" dediğimizde α 0.05'e (%5'e) eşittir. Standart normal dağılımda ise Z_α/2 şeklinde gösteririz ve güven katsayısı olarak adlandırırız.

Standart normal dağılımda Z_0.05/2 değeri yani z olasılığının
%95/2 = 0.4750 olduğu durum

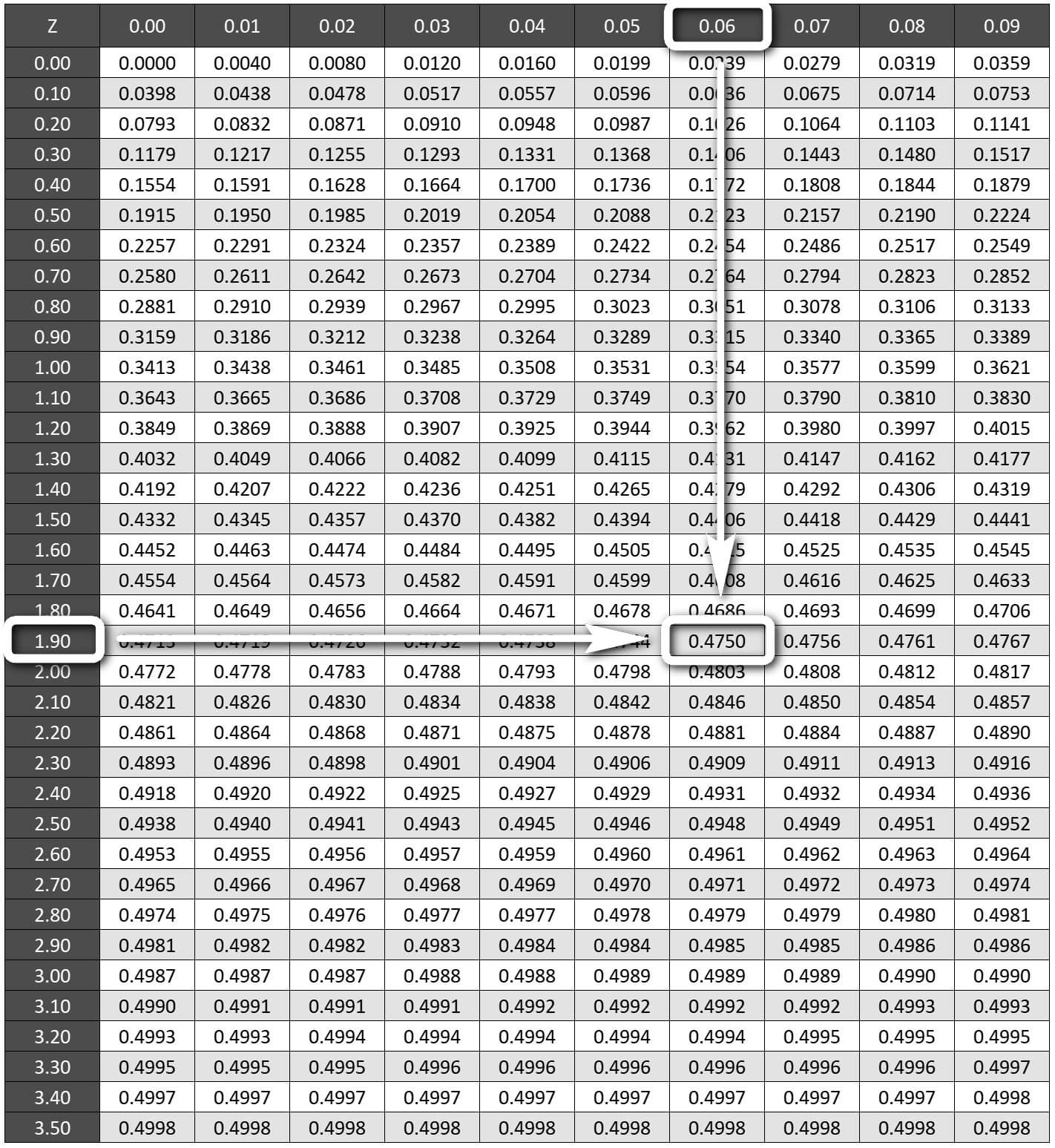
1.90 ve 0.06 eksenlerinin kesiştiği hücredir. Diğer bir ifade ile z değeri 1.96'dır.

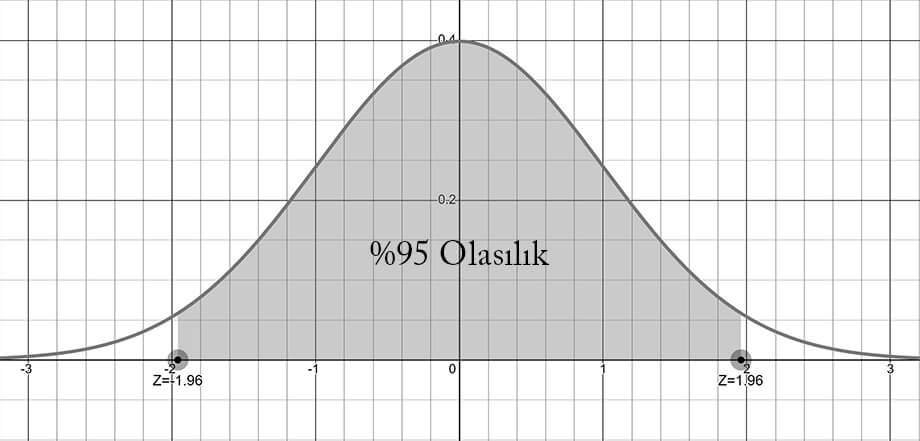
Standart normal dağılım grafiğine baktığımızda %95 olasılığın -1.96 ve 1.96 z değerleri arasında kalan alan olduğunu görebiliriz.

α'nın %1'e eşit olduğu durumda Z_0.01/2 olasılığı %99/2 = 0.4950'dir.

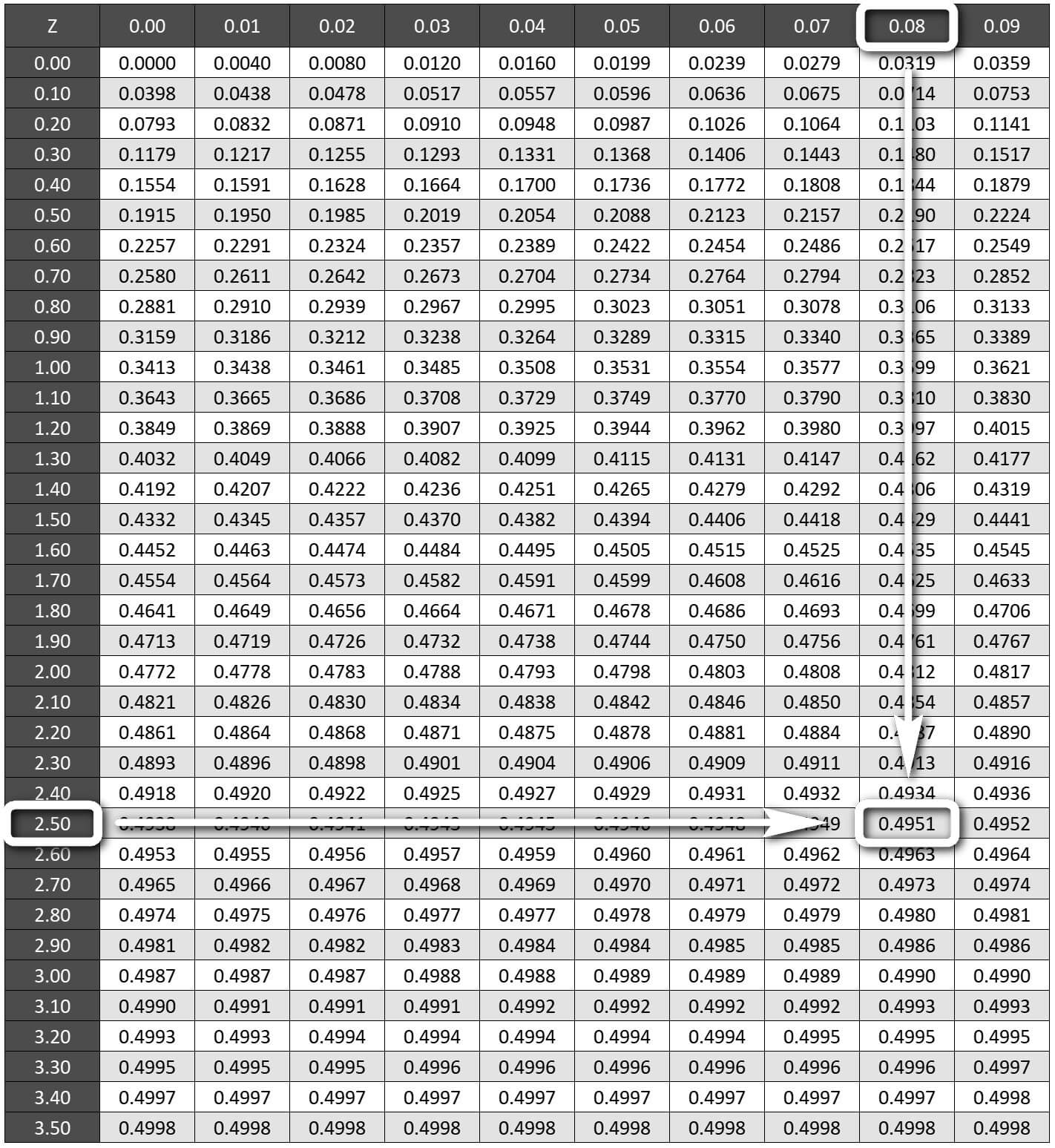
0.4950'ye en yakın hücre 2.50 ve 0.08 eksenlerinin kesiştiği hücre olan 0.4951'dir. z değeri bu nedenle 2.58'e eşittir.

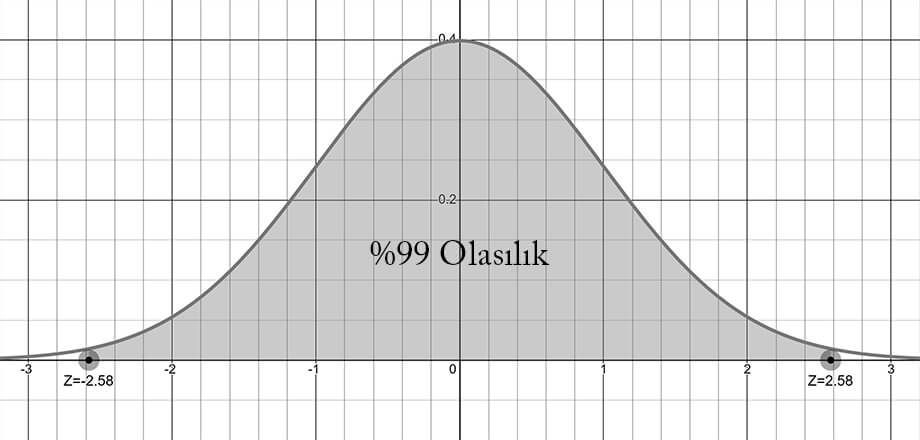
Standart normal dağılım grafiğinde %99 olasılığın -2.58 ve 2.58 z değerleri arasında kalan alan olduğunu görebiliriz.

Görüldüğü üzere olasılık düzeyi arttıkça tahmin etmek kolaylaşmaktadır. İstatistikte çoğunlukla α'nın 0.05 olduğu durum, yani %95 güven düzeyi kullanılmaktadır.

α (alfa) istatistikte önem seviyesi (significance level), anlamlılık seviyesi, kritik p-değeri (critical p-value) anlamlarına gelmektedir. İlerleyen bölümlerde öğreneceğimiz hipotez testleri dahil birçok konuda α önem seviyesi kavramı sıkça kullanılacaktır. R.A. Fisher tarafından literatüre kazandırılmıştır.

Anakütle standart sapması (σ) bilindiğinde güven aralığı

\[ \bar X \pm Z_{\alpha/2} \cdot { \sigma \over \sqrt{n} } \]

ile ifade edilir.

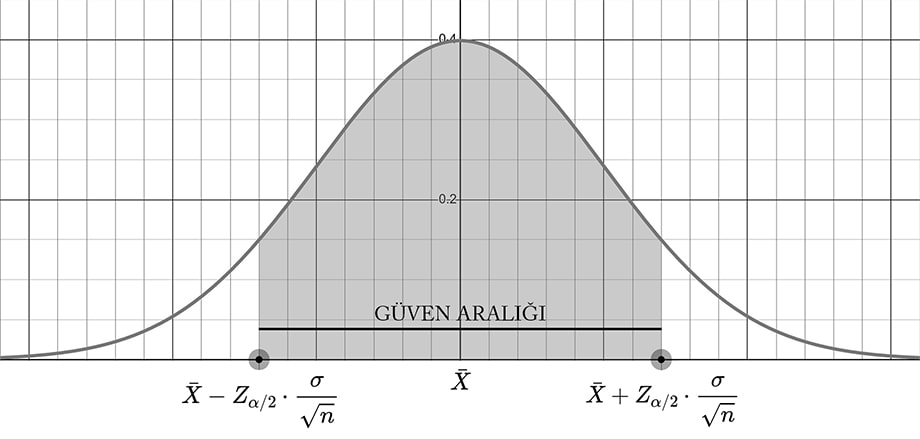
Grafik üzerinde güven aralığını görseldeki gibi gösterebiliriz. Burada

\[ Z_{\alpha/2} \cdot { \sigma \over \sqrt{n} } \]

ifadesi tahmin hatası olarak adlandırılmaktadır.

Anakütle standart sapması (σ) bilinmediğinde güven aralığı

\[ \bar X \pm Z_{\alpha/2} \cdot { s \over \sqrt{n} } \]

ile ifade edilir. σ yerine örneklem standart sapması (s) kullanılır.

\[ P ( \bar X - Z_{\alpha/2} \cdot { s \over \sqrt{n} } \le \mu \le \bar X + Z_{\alpha/2} \cdot { s \over \sqrt{n} } ) = 1 - \alpha \]

Güven aralığının olasılık fonksiyonudur.

Uygulama: Bir anakütleden 100 birimlik bir örneklem seçilmiş ve ortalaması 36, standart sapması 8 bulunmuştur.

Anakütle ortalaması için %95 düzeyinde güven aralığını bulunuz.
En az kaç birimlik örnek alınmalı ki tahmin hatası 2'den az olsun.

Yanıt 1: %95 güven düzeyinde aralık tahmini yapılacağı için Z_0.05/2 = 1.96 güven katsayısı kullanılacaktır. Ayrıca anakütlenin standart sapmasını bilmemekteyiz.

\[ \bar X \pm Z_{\alpha/2} \cdot { s \over \sqrt{n} } \]

Formülü uyguladığımızda

\[ 36 \pm 1.96 \cdot { 8 \over \sqrt{100} } \]

\[ 36 \pm 1.5680 \]

güven aralığını buluruz. 36'dan 1.5680 çıkarıp 1.5680 eklediğimizde

\[ P(34.43 < \mu < 37.57) = 0.95 \]

olasılık fonksiyonunu elde ederiz. %95 olasılıkla anakütle ortalaması 34.43 ve 37.57 aralığındadır diyebiliriz.

Yanıt 2: Tahmin hatasını

\[ Z_{\alpha/2} \cdot { s \over \sqrt{n} } \]

olarak ifade etmiştik. Bizden bu hatanın

\[ Z_{\alpha/2} \cdot { s \over \sqrt{n} } < 2 \]

2'den küçük olması için en az kaç birimlik bir örneklem oluşturmamız gerektiği sorulmaktadır.

\[ 1.96 \cdot { 8 \over \sqrt{n} } < 2 \]

Örneğimizde bu ifadeyi uyguladığımızda yukarıdaki denklemini elde ederiz.

\[ 1.96 \cdot { 8 \over 2 } < \sqrt{n} \]

Aynı ifadeyi şeklinde de gösterebiliriz.

\[ 7.84 < \sqrt{n} \] \[ {7.84}^2 < (\sqrt{n})^2 \] \[ 61.47 < n \]

Özetle anakütle ortalamasını tahmin hatası 2'den az olacak şekilde tahmin etmek istersek en az 62 birimden oluşan bir örneklem kullanmak durumundayız. Biz ise 100 birimden oluşan bir örneklem kullandığımız için tahmin hatası 2'den az olacaktır.

Uygulama: Şimdi Normal Dağılım bölümünde de kullandığımız gerçek bir örnek üzerinden gidelim.

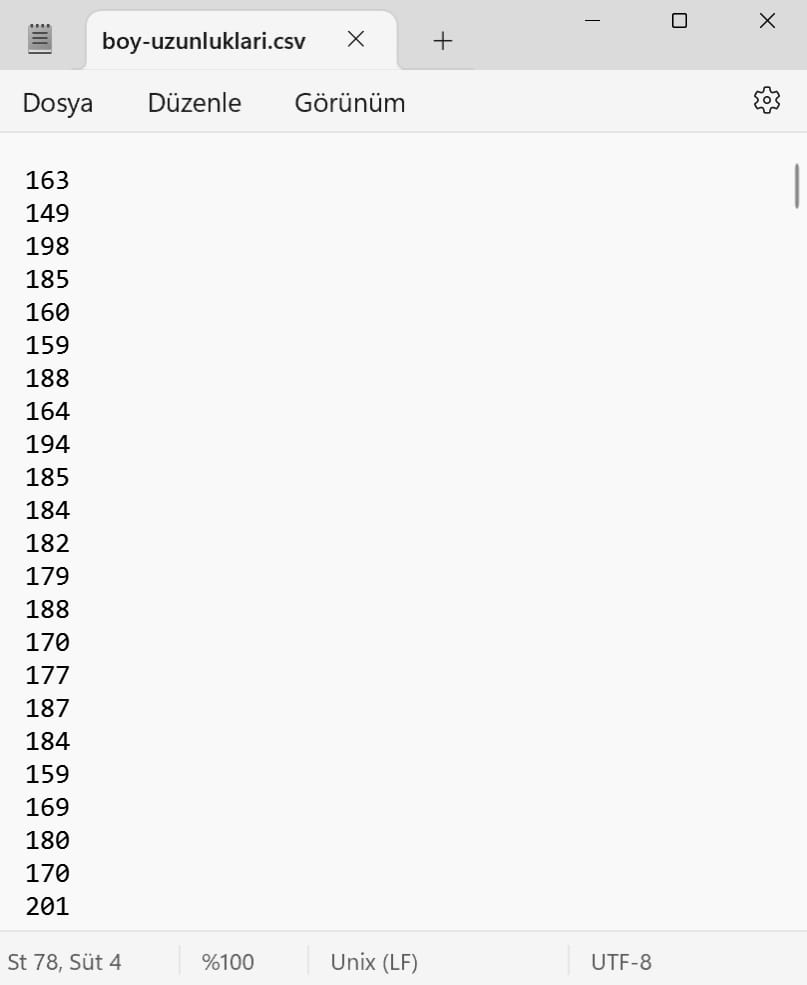
Boy uzunlukları csv dosyasını kullanacağız.

Boy Uzunlukları (CSV)

csv dosyasını indirmek için yukarıdaki bağlantıyı kullanabilirsiniz.

1200 veri biriminden oluşan, ortalaması 175.71 ve standart sapması 13.70 olan bir anakütlemiz var. Anakütle ortalamasını ve standart sapmasını bilmediğimizi varsayalım.

Bu anakütleden

198, 179, 201, 165, 183, 191, 171, 199, 190, 178, 180, 172, 171, 177, 185, 184, 165, 181, 188, 178, 157, 171, 191, 157, 188, 181, 167, 180, 159, 168, 181, 155, 174, 159, 188, 185, 160, 154, 183, 179, 162, 151, 165, 182, 175, 152, 153, 152, 177, 206, 188, 161, 198, 211, 187, 189, 151, 173, 153, 154, 196, 190, 188, 172, 164, 182, 167, 166, 183, 171, 174, 177, 174, 170, 182, 145, 179, 176, 174, 194, 177, 185, 174, 176, 166, 164, 190, 183, 162, 176, 182, 175, 174, 203, 166, 153, 166, 181, 156, 183, 191, 165, 186, 150, 198, 173, 155, 182, 158, 181, 195, 170, 149, 183, 154, 191, 176, 151, 168, 191

birimden oluşan 120 birimlik bir örneklem seçelim. Bakalım %95 olasılıkla anakütle ortalamasını hangi aralıkta bulacağız. Anakütle ortalamasının ve standart sapmasının bilinmediğini varsaydığımızı tekrar hatırlatırım. Örneklemin ortalaması X̄ = 174.97, standart sapması (s) = 1.30'dur.

Formülü uyguladığımızda

\[ \bar X \pm Z_{\alpha/2} \cdot { s \over \sqrt{n} } \] \[ 174.97 \pm 1.96 \cdot { 1.30 \over \sqrt{120} } \] \[ 174.97 \pm 0.2326 \]

ifadesini elde ederiz. 174.97'ye 0.2326'yı ekleyip çıkardığımızda

\[ P(174.73 < \mu < 175.20) = 0.95 \]

güven aralığını elde ederiz. %95 olasılıkla anakütle ortalaması 174.73 ve 175.20 arasındadır. Anakütle ortalaması gerçekte 175.71'dir. Doğru aralıkta tahmin edemedik fakat anakütle ortalamasına çok yakın bir değer bulduk.

Student t-Dağılımı

Örneklem 30'dan küçük olduğu durumda (n < 30 durumunda)
z-Dağılımı yerine Student t-Dağılımı kullanılır. Kısaca t-Dağılımı olarak adlandırılır.

t-Dağılımı ilk olarak 1908 yılında İrlanda'da Guinness Bira fabrikasında çalışan William Sealy Gosset'in küçük örneklemler üzerine yayınladığı makalesinde ortaya konmuştur. O yıllarda şirket sırlarının açığa çıkmasını önlemek amacıyla bilimsel yayınların yasak olmasından dolayı Gosset yayınladığı makalede adını Student (öğrenci) olarak gizlemiştir. Her ne kadar makalesinde t yerine z harfini kullansa da ilerleyen yıllarda teori Ronald Aylmer Fisher¹ tarafından geliştirilmiş ve bugünkü bildiğimiz adıyla Student t-Dağılımı (Student's t-distribution) ortaya çıkmıştır.

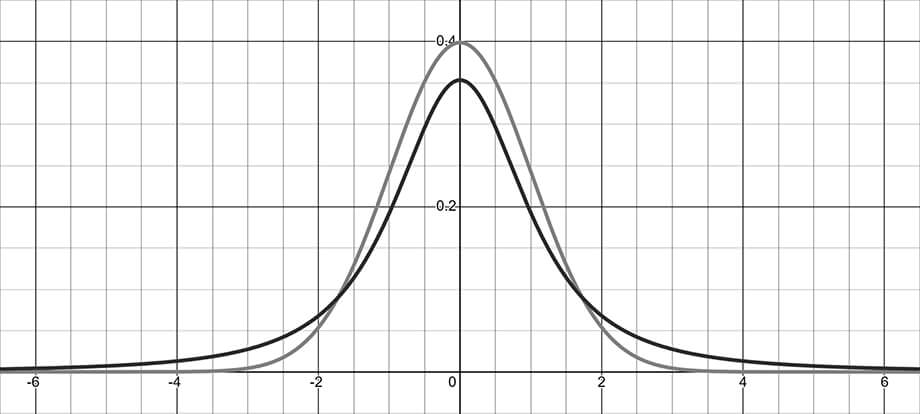
t-Dağılımı z-Dağılımına (standart normal dağılıma) çok benzer. Yukarıdaki görselde 3 birimden oluşan ve koyu renk ile gösterilen eğri t-Dağılımına ait eğridir. Açık renk ile gösterilen eğri ise z-Dağılımı eğrisidir. Örneklem sayısı 30'un üzerine çıktıkça t-Dağılımı eğrisi z-Dağılımı eğrisiyle neredeyse aynı olmaktadır. Birim sayısı 30'un altına indiğinde ise t-Dağılımı eğrisi basıklaşmaktadır.

t-Dağılımında v notasyonu ile serbestlik derecesi gösterilir.

\[ v = n - 1 \]

Serbestlik derecesi daima örneklem sayısının 1 eksiğidir.

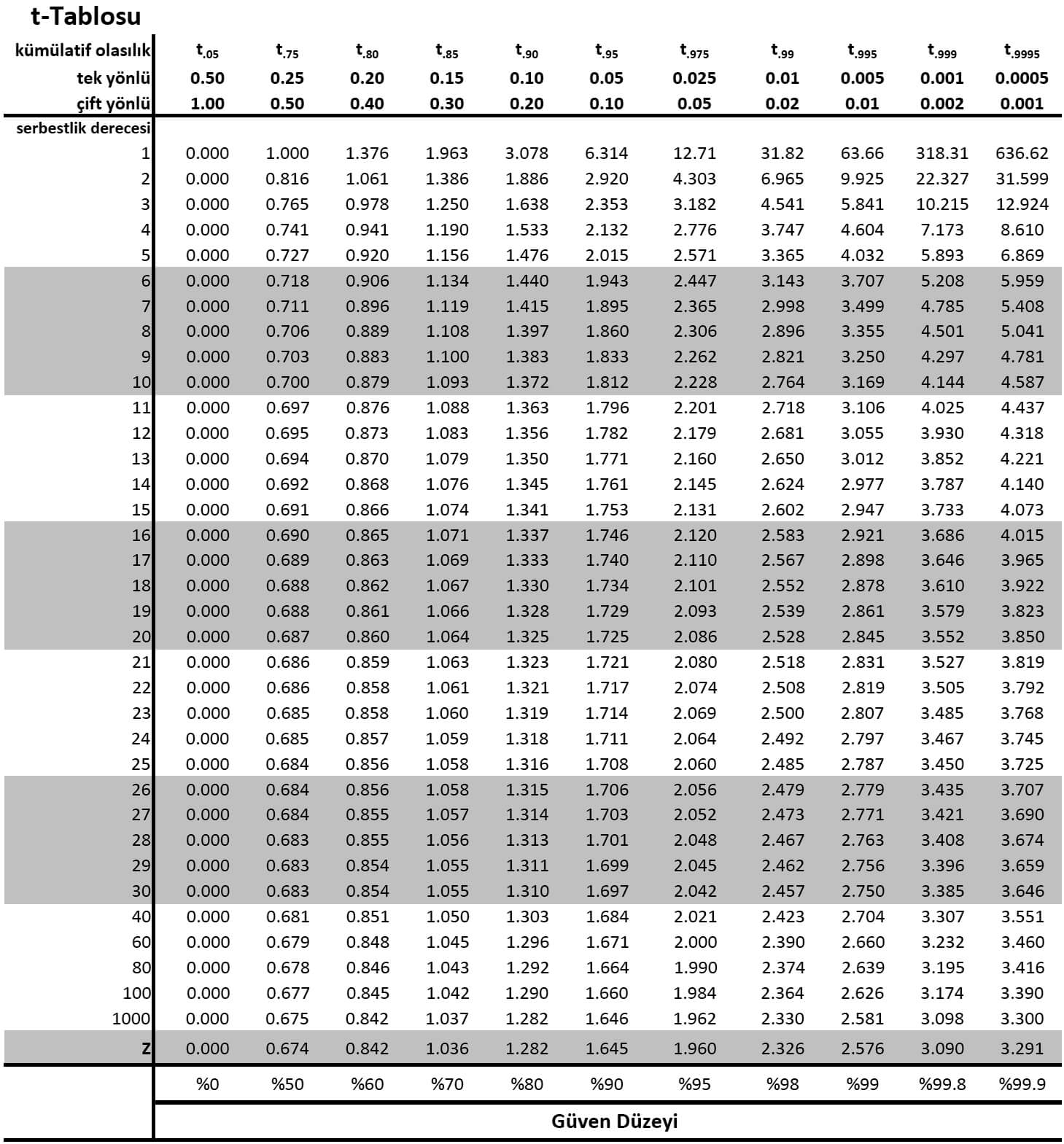
t-Tablosu görseldeki gibidir. Tablonun y eksen başlıklarında serbestlik dereceleri (v), x eksen başlıklarında (sütun başlıklarında) α değerleri yer alır. Tablonun altına dikkat edilirse örneklem sayısı (serbestlik derecesi) arttıkça t olasılıkları z olasılıklarına yakınsamaktadır.

t-Tablosu (PDF)

t-Tablosu için yukarıdaki bağlantıya tıklayabilir ve PDF formatında indirebilirsiniz. Renk ve font düzenlemeleri yapmak isterseniz bu bağlantıya tıklayabilir, Excel formatında indirebilirsiniz.

t-Dağılımı için Güven Aralığı

z-Dağılımı öncelikle

\[ { \bar x - \mu } \over { s \over { \sqrt{v} } } \]

ile t-Dağılımına dönüştürülür.

\[ P ( -t_{\alpha/2;v} \le { { \bar x - \mu } \over { s \over { \sqrt{v} } } } \le t_{\alpha/2;v} ) = 1 - \alpha \]

t-Dağılımı olasılık fonksiyonu yazılır. Ardından anakütle ortalaması (μ)

\[ P ( \bar x - t_{\alpha/2;v}{ s \over { \sqrt{v} } } \le \mu \le \bar x + t_{\alpha/2;v}{ s \over { \sqrt{v} } } ) = 1 - \alpha \]

yalnız bırakılır ve t-Dağılımı yukarıdaki olasılık formülü ile gösterilir.

Uygulama: Bir anakütleden 19 birim örnek seçilmiş ve örneklem ortalaması 64, standart sapması 12 bulunmuştur. %95 güven düzeyinde anakütle ortalaması için güven aralığını bulunuz.

Yanıt: Öncelikle sorudaki değerleri formülümüze uygulayalım:

\[ P ( \bar x - t_{\alpha/2;v}{ s \over { \sqrt{v} } } \le \mu \le \bar x + t_{\alpha/2;v}{ s \over { \sqrt{v} } } ) = 1 - \alpha \] \[ P ( 64 - t_{0.05/2;18}{ 12 \over { \sqrt{18} } } \le \mu \le 64 + t_{0.05/2;18}{ 12 \over { \sqrt{18} } } ) = 1 - 0.05 \] \[ P ( 64 - t_{0.025;18}{ 12 \over { \sqrt{18} } } \le \mu \le 64 + t_{0.025;18}{ 12 \over { \sqrt{18} } } ) = 0.95 \]

t_0.025;18 olasılığı için t-Tablosunu kullanmalıyız.

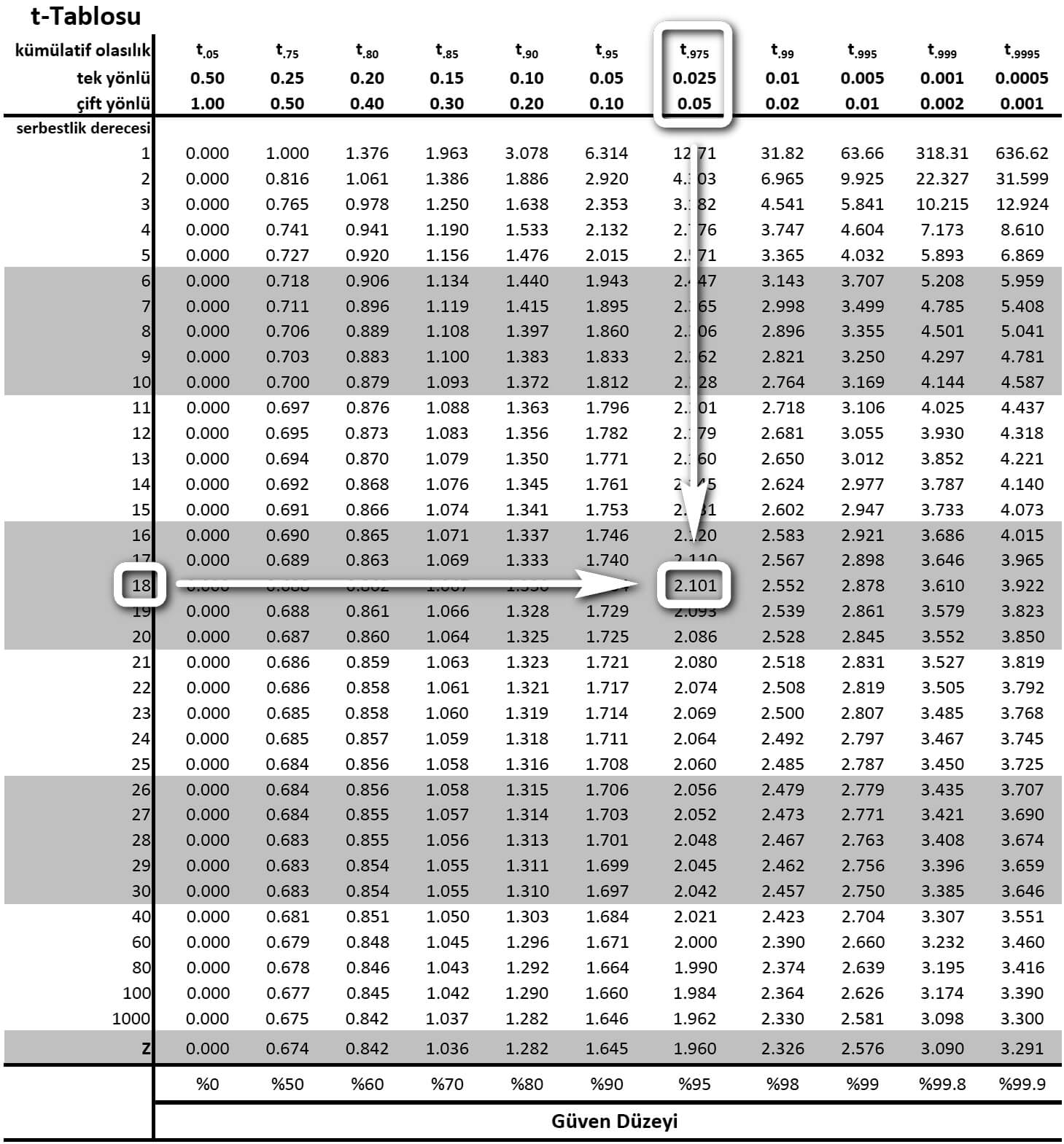
Anakütleden 19 birim seçilmiştir. Serbestlik derecesi (v)

\[ v = n - 1 = 19 - 1 \]

18'dir. Bu nedenle tabloda serbestlik derecesinin 18 ve α'nın 0.05 olduğu eksenlerin kesiştiği hücre t_0.025;18 olasılığını verir. Bu hücre 2.101'dir.

\[ P ( 64 - 2.101 { 12 \over { \sqrt{18} } } \le \mu \le 64 + 2.101 { 12 \over { \sqrt{18} } } ) = 0.95 \] \[ P ( 64 - 5.9425 \le \mu \le 64 + 5.9425 ) = 0.95 \] \[ P ( 58.06 \le \mu \le 69.94 ) = 0.95 \]

%95 olasılıkla anakütle ortalaması 58.06 ve 69.94 arasında bir değerdir diyebiliriz.

Uygulama: Bir anakütleden 25 birim örnek seçilmiş ve örneklem ortalaması 46, standart sapması 4.76 bulunmuştur. %95 güven düzeyinde anakütle ortalaması için güven aralığını bulunuz.

Yanıt: Sorudaki değerleri olasılık formülümüze uyarlayalım:

\[ P ( \bar x - t_{\alpha/2;v}{ s \over { \sqrt{v} } } \le \mu \le \bar x + t_{\alpha/2;v}{ s \over { \sqrt{v} } } ) = 1 - \alpha \] \[ P ( 46 - t_{0.05/2;24}{ 4.76 \over { \sqrt{24} } } \le \mu \le 46 + t_{0.05/2;24}{ 4.76 \over { \sqrt{24} } } ) = 1 - 0.05 \] \[ P ( 46 - t_{0.025;24}{ 4.76 \over { \sqrt{24} } } \le \mu \le 46 + t_{0.025;24}{ 4.76 \over { \sqrt{24} } } ) = 0.95 \]

t_0.025;24 olasılığı için t-Tablosuna bakalım.

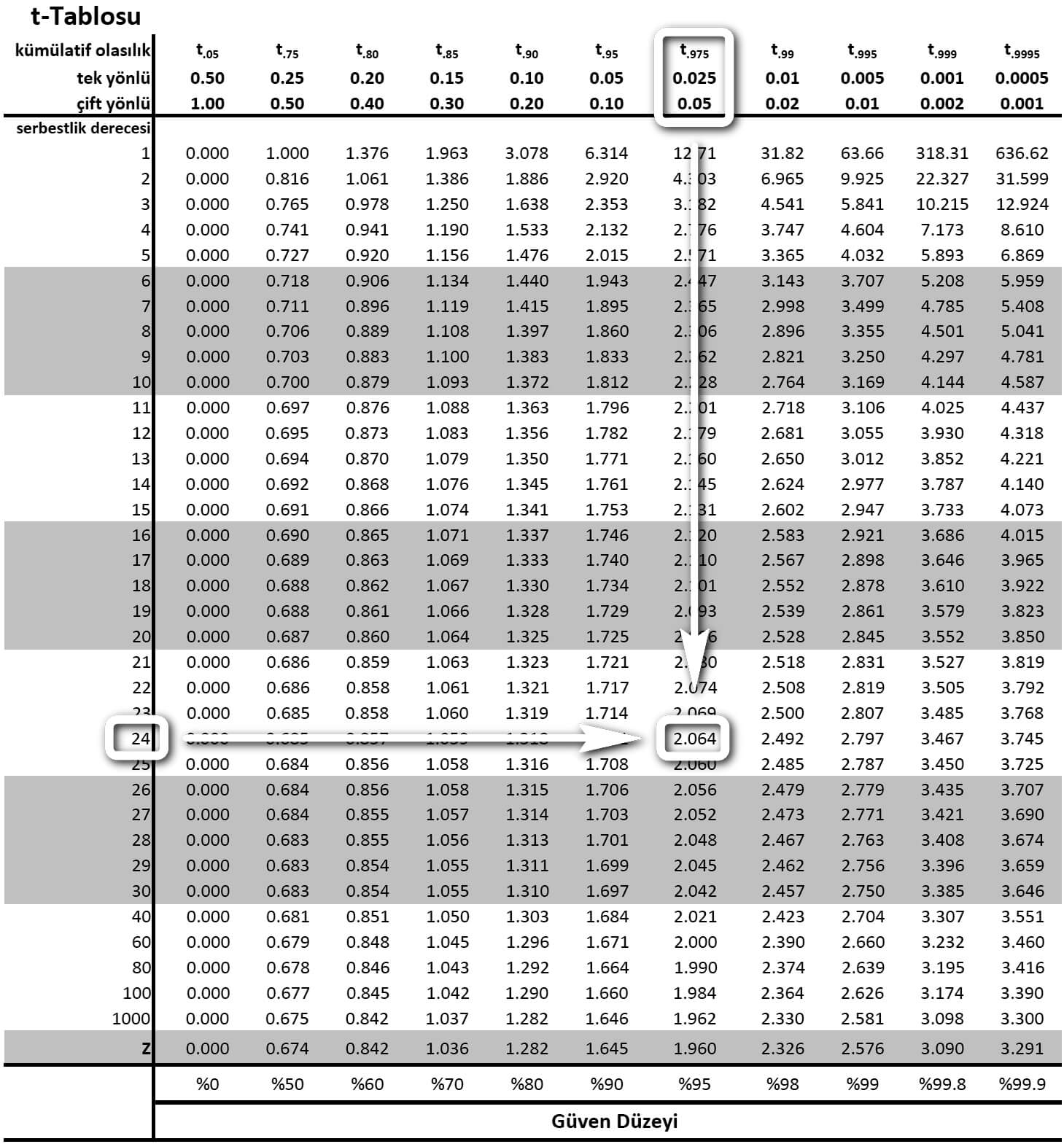
Serbestlik derecesi 24 olan satır ile α değerinin 0.05 olduğu sütunun kesiştiği hücre t_0.025;24 olasılığını verir. Bu hücre 2.064'tür.

\[ P ( 46 - t_{0.025;24}{ 4.76 \over { \sqrt{24} } } \le \mu \le 46 + t_{0.025;24}{ 4.76 \over { \sqrt{24} } } ) = 0.95 \] \[ P ( 46 - 2.064 { 4.76 \over { \sqrt{24} } } \le \mu \le 46 + 2.064 { 4.76 \over { \sqrt{24} } } ) = 0.95 \] \[ P ( 46 - 2.0054 \le \mu \le 46 + 2.0054 ) = 0.95 \] \[ P ( 44.01 \le \mu \le 48.01 ) = 0.95 \]

%95 olasılıkla anakütle ortalaması 44.01 ve 48.01 arasındadır.

Uygulama: Bir anakütleden 13 birim örnek seçilmiş ve örneklem ortalaması 27.14, standart sapması 6.73 bulunmuştur. %99 güven düzeyinde anakütle ortalaması için güven aralığını bulunuz.

Yanıt: Sorudaki değerleri olasılık formülümüze uyarlayalım:

\[ P ( \bar x - t_{\alpha/2;v}{ s \over { \sqrt{v} } } \le \mu \le \bar x + t_{\alpha/2;v}{ s \over { \sqrt{v} } } ) = 1 - \alpha \] \[ P ( 27.14 - t_{0.01/2;12}{ 6.73 \over { \sqrt{12} } } \le \mu \le 27.14 + t_{0.01/2;12}{ 6.73 \over { \sqrt{12} } } ) = 1 - 0.01 \] \[ P ( 27.14 - t_{0.005;12}{ 6.73 \over { \sqrt{12} } } \le \mu \le 27.14 + t_{0.005;12}{ 6.73 \over { \sqrt{12} } } ) = 0.99 \]

Örnekte %99 güven düzeyinin sorulduğuna dikkat edelim.

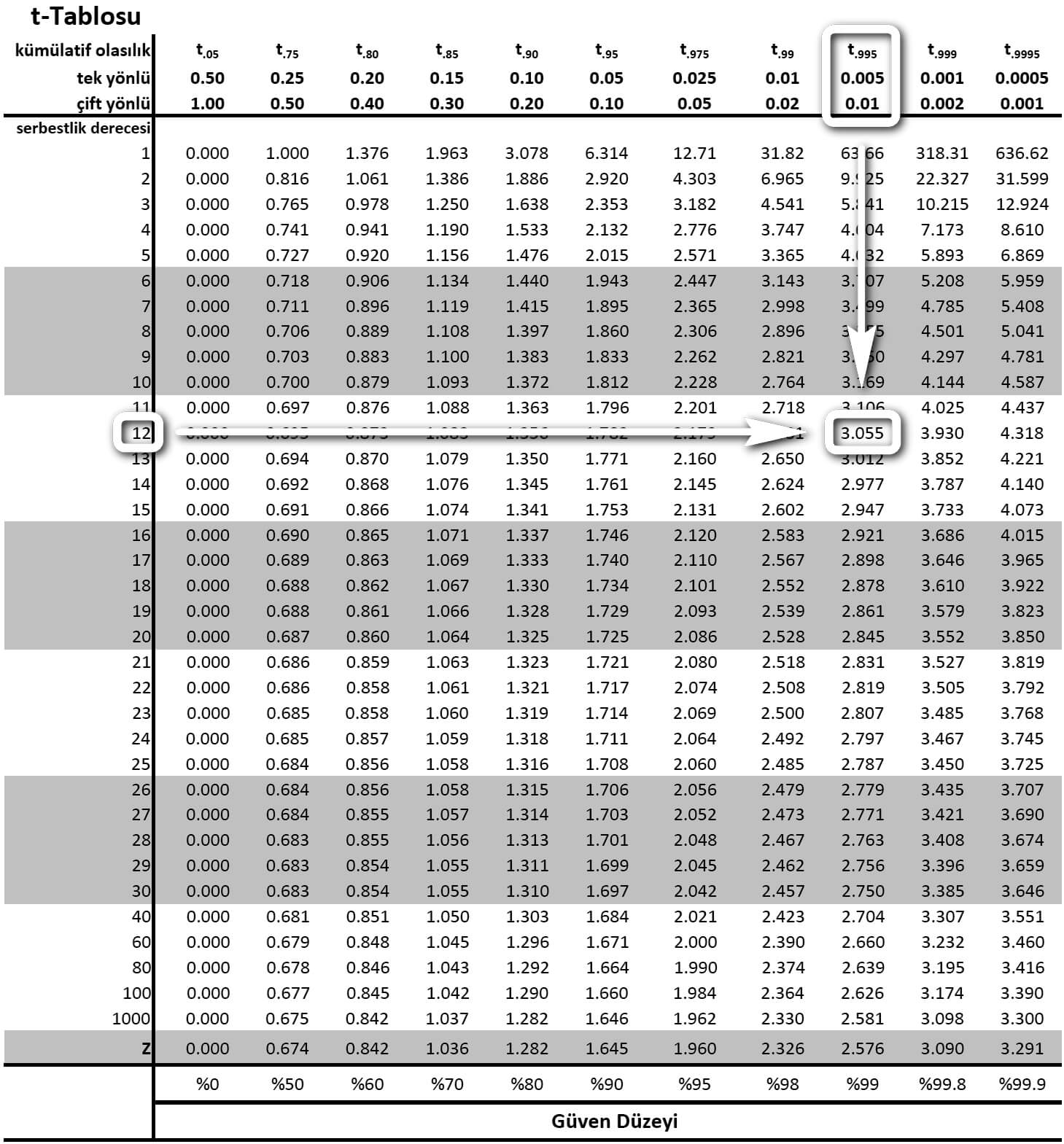
Serbestlik derecesi 12 olan satır ile α değerinin 0.01 olduğu sütunun kesiştiği hücredeki t_0.005;12 olasılığı 3.055'tir.

\[ P ( 27.14 - t_{0.005;12}{ 6.73 \over { \sqrt{12} } } \le \mu \le 27.14 + t_{0.005;12}{ 6.73 \over { \sqrt{12} } } ) = 0.99 \] \[ P ( 27.14 - 3.055 { 6.73 \over { \sqrt{12} } } \le \mu \le 27.14 + 3.055 { 6.73 \over { \sqrt{12} } } ) = 0.99 \] \[ P ( 27.14 - 5.9352 \le \mu \le 27.14 + 5.9352 ) = 0.99 \] \[ P ( 21.20 \le \mu \le 33.08 ) = 0.99 \]

%99 olasılıkla anakütle ortalaması 21.20 ve 33.08 arasındadır.

SPSS'te Güven Aralığı

SPSS'te güven aralığı oluşturması oldukça basittir.²

Güven Aralığı Örnek Veri (Excel)

Öncelikle güven aralığı için kullanacağımız örnek verinin Excel dosyasını indirelim.

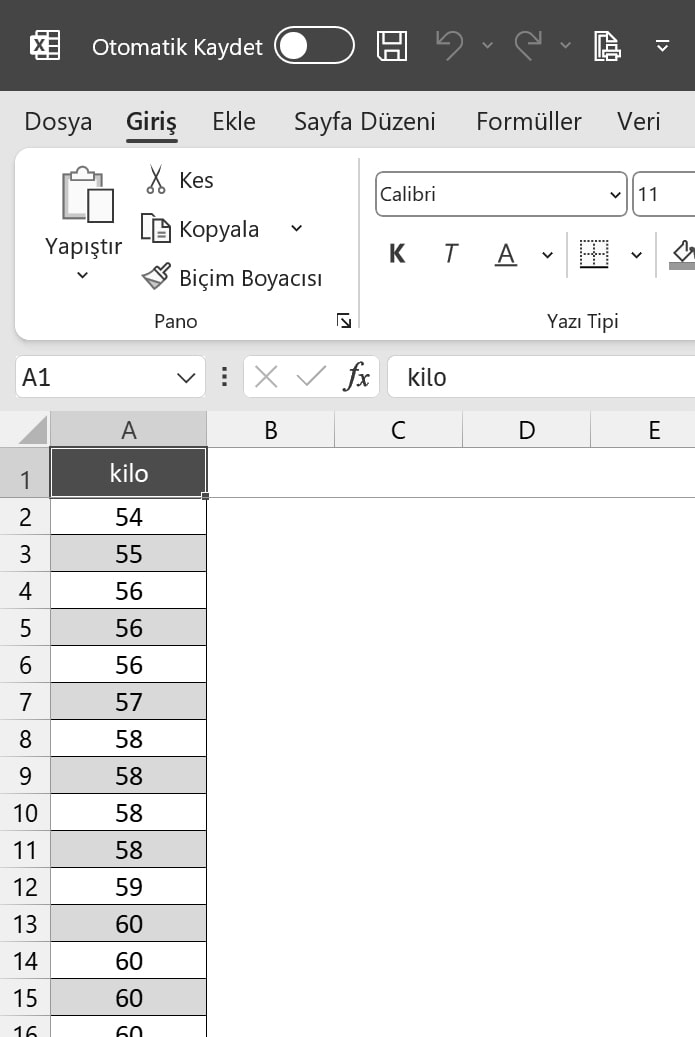
Excel dosyamız görseldeki gibi açılmış olmalıdır. 80 adet kilo verisi bulunmaktadır. Başlık hariç tüm verileri seçelim ve kopyalalım.

SPSS'te ilk hücreye kopyaladığımız verileri yapıştıralım. Sayfa altındaki Variable View sekmesinden sütun başlığını değiştirebilir, ondalık gösterimini (decimals'ı) sıfırlayabilirsiniz.

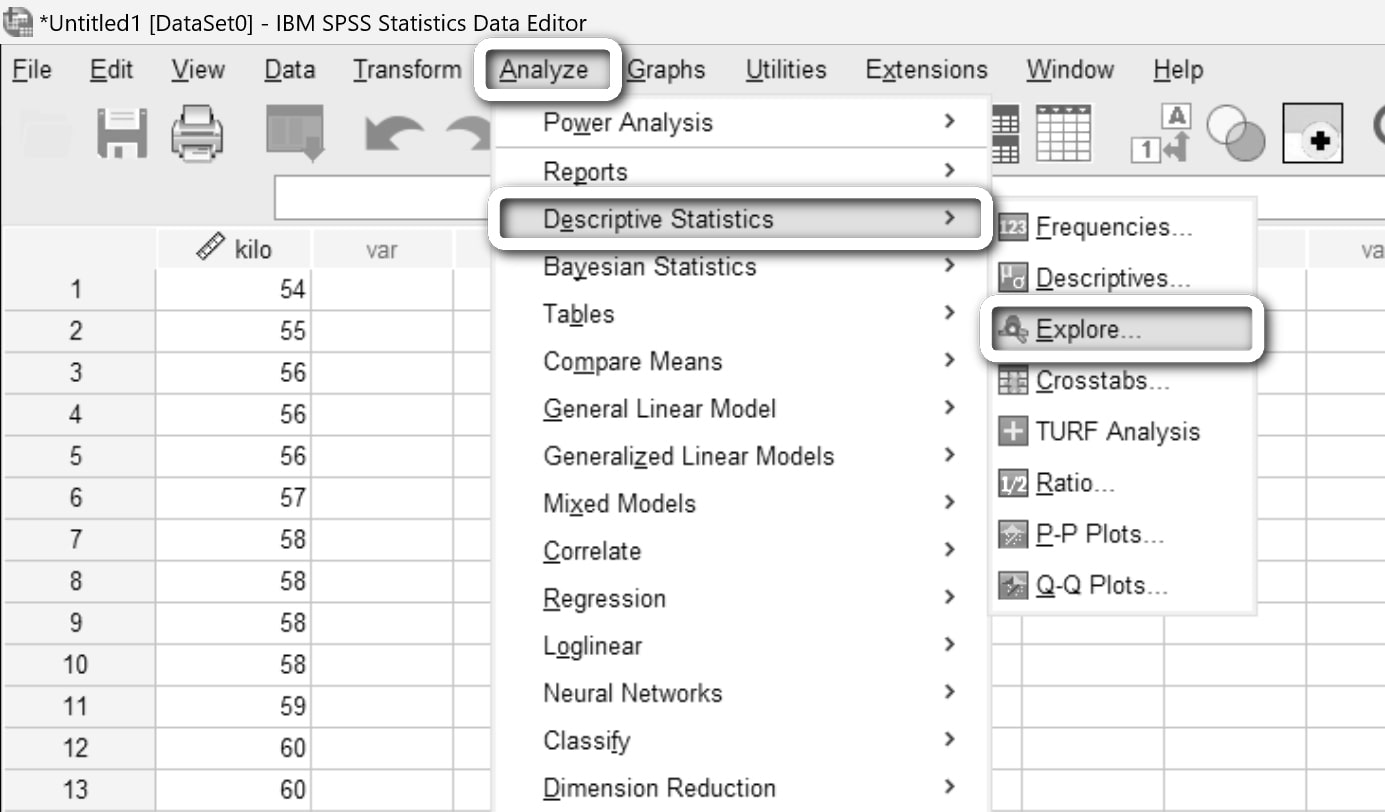
Menüden Analyze > Descriptive Statistics > Explore... yolunu izleyelim.

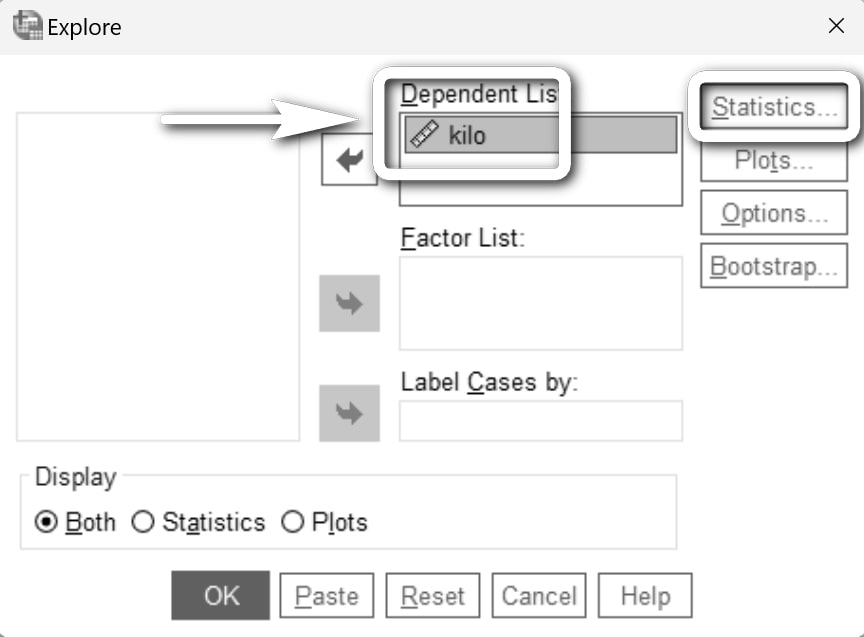
kilo değişkenini Dependent List (Bağımlı Liste) alanına gönderelim. Ardından Statistics... düğmesine tıklayalım.

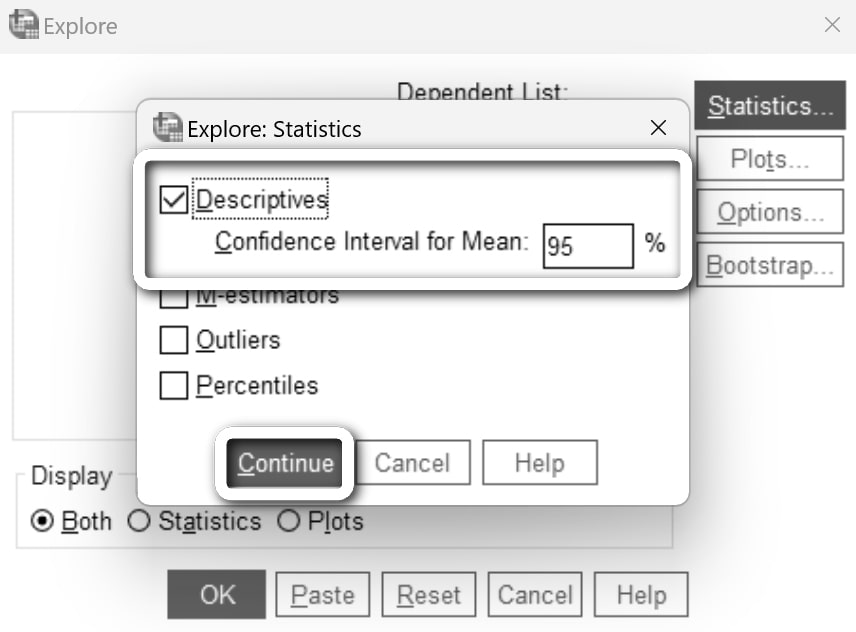
Güven düzeyinin %95 olduğuna emin olduktan sonra Continue diyelim.

OK tuşuna tıklayalım.

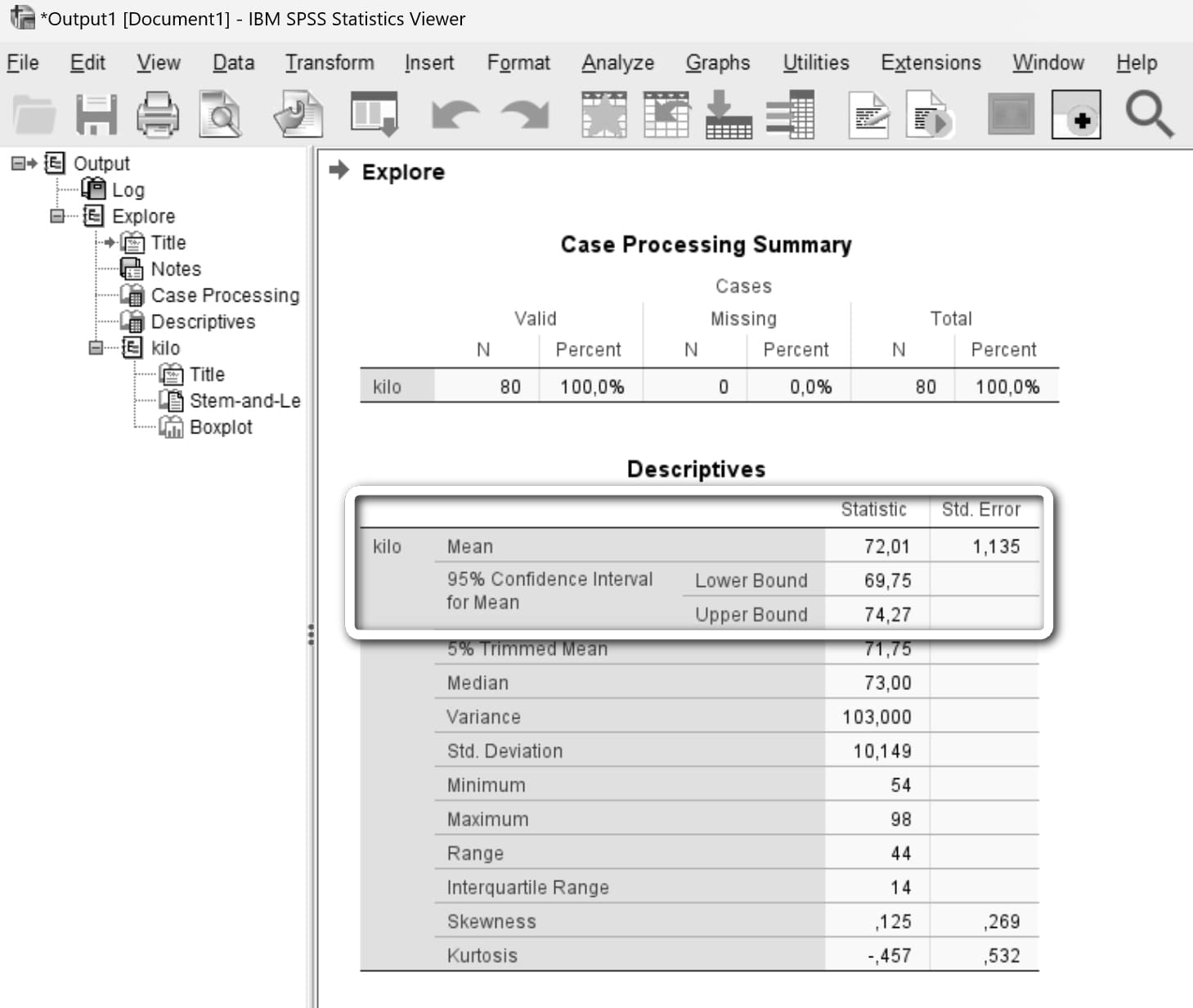
Output penceresi açılacaktır. 80 veriden oluşan örneğimizde ortalama 72.01'dir. Anakütle ortalaması %95 olasılıkla 69.75 - 74.27 arasındadır.

Güven aralığı ve Student t-Dağılımı istatistikte bu şekilde kullanılmaktadır. Şimdi biraz pratik yapalım ve bu bölümde öğrendiklerimizi pekiştirelim.

Python'da Güven Aralığı

Python ile hem z-Dağılımı hem de t-Dağılımı için güven aralığı hesaplanabilir.

z-Dağılımı için Güven Aralığı

z-Dağılımı için güven aralığı hesaplamak için aşağıdaki kodları kullanmalıyız.

z-Dağılımı için öncelikle scipy kütüphanesini import etmeliyiz. Kütüphane eklemek daha kolay olduğu için Visual Studio Code yerine PyCharm kullanmanızı öneririm.

Daha önce çözdüğümüz "Bir anakütleden 100 birimlik bir örneklem seçilmiş ve ortalaması 36, standart sapması 8 bulunmuştur. Anakütle ortalaması için %95 düzeyinde güven aralığını bulunuz." sorusunun Python kodları yukarıdaki gibidir. Yanıt

%95 güven düzeyinde güven aralığı: (34.43, 37.57)

şeklinde olacaktır. Kodlardaki örneklem büyüklüğü, örneklem ortalaması ve örneklem standart sapması değerlerini değiştirip farklı soruların yanıtlarını bulabiliriz.

t-Dağılımı için Güven Aralığı

t-Dağılımı için güven aralığı hesaplamak için aşağıdaki kodları kullanmalıyız.

t-Dağılımı için de scipy kütüphanesini import etmeliyiz.

Daha önce çözdüğümüz "Bir anakütleden 19 birim örnek seçilmiş ve örneklem ortalaması 64, standart sapması 12 bulunmuştur. %95 güven düzeyinde anakütle ortalaması için güven aralığını bulunuz." sorusunun Python kodları yukarıdaki gibidir. Yanıt

%95 güven düzeyinde güven aralığı: (58.22, 69.78)

şeklinde olacaktır.

Sıra Sizde

Uygulama: 21,470 çalışanı olan bir firmadan 140 çalışan seçilmiş ve çalışanların ağırlıkları ortalama 72 kg, standart sapması 8.9 kg bulunmuştur. Firmadaki tüm çalışanlara ait ortalama ağırlığın güven aralığını %95 güven düzeyinde bulunuz.

Yanıtı Göster

Anakütleden 140 birim ile örnekleme yapılmıştır. 30'un üzerinde birim seçildiği için z-Dağılımı için güven aralığı oluşturmalıyız. %95 güven düzeyinde z değeri 1.96'dır.

\[ \bar X \pm Z_{\alpha/2} \cdot { s \over \sqrt{n} } \] \[ 72 \pm 1.96 \cdot { 8.9 \over \sqrt{140} } \] \[ 72 \pm 1.4743 \]

Güven aralığını sınırılarını belirledikten sonra olasılık fonksiyonunu oluştururuz.

\[ P(70.53 < \mu < 73.47) = 0.95 \]

%95 olasılıkla tüm firma çalışanların ağırlık ortalaması 70.53 ve 73.47 kg arasındadır.

Uygulama: 640 öğrencinin girdiği bir sınavdan 27 öğrenci seçilmiştir. Sınav not ortalamaları 72, standart sapması 14'tür. Tüm öğrencilerin ortalama sınav notlarının güven aralığını bulunuz. (α = 0.05)

Yanıtı Göster

27 öğrenciden oluşan bir örneklem seçildiği için t-Dağılımı için güven aralığı oluşturmalıyız. Serbestlik derecesi v = 27 - 1'den 26'dır. α (alfa) değeri 0.05 verildiği için %95 güven düzeyinde güven aralığı oluşturmalıyız.

\[ P ( \bar x - t_{\alpha/2;v}{ s \over { \sqrt{v} } } \le \mu \le \bar x + t_{\alpha/2;v}{ s \over { \sqrt{v} } } ) = 1 - \alpha \] \[ P ( 72 - t_{0.05/2;26}{ 14 \over { \sqrt{26} } } \le \mu \le 72 + t_{0.05/2;26}{ 14 \over { \sqrt{26} } } ) = 1 - 0.05 \] \[ P ( 72 - t_{0.025;26}{ 14 \over { \sqrt{26} } } \le \mu \le 72 + t_{0.025/2;26}{ 14 \over { \sqrt{26} } } ) = 0.95 \]

Olasılık fonksiyonunu oluşturduk. t-Tablosuna bakalım:

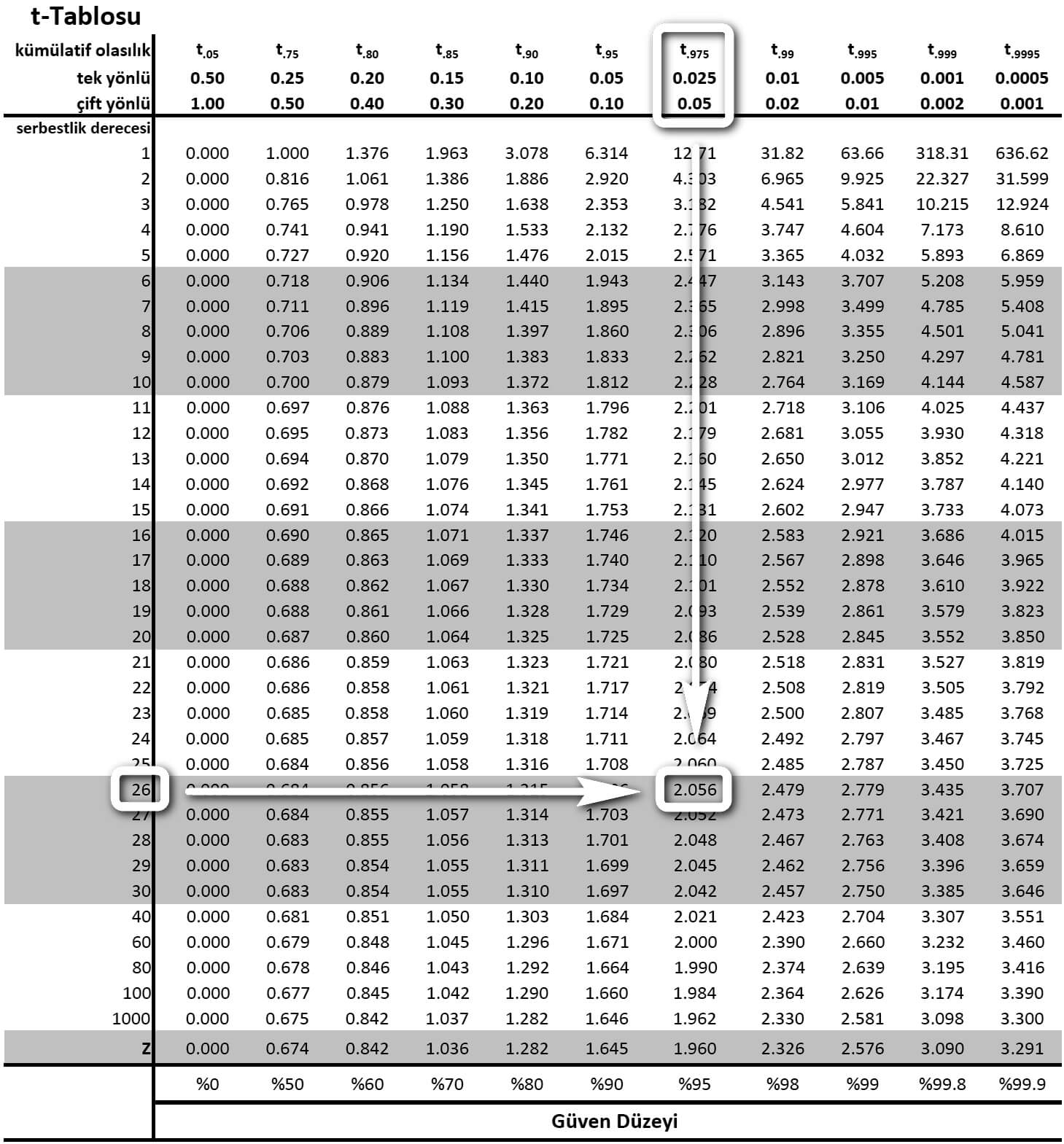
Serbestlik derecesi 26 olan satır ile α değerinin 0.05 olduğu sütunun kesiştiği hücredeki t_0.025;26 olasılığı 2.056'dır.

\[ P ( 72 - 2.056 { 14 \over { \sqrt{26} } } \le \mu \le 72 + 2.056 { 14 \over { \sqrt{26} } } ) = 0.95 \] \[ P ( 72 - 5.6450 \le \mu \le 72 + 5.6450 ) = 0.95 \] \[ P ( 66.36 \le \mu \le 77.65 ) = 0.95 \]

%95 olasılıkla 640 öğrencinin not ortalaması 66 ve 78 arasındadır.

1 R.A. Fisher istatistik alanında oldukça popülerdir. (bkz. wikipedia)
2 IBM SPSS Statistics | version 27.0.1.0

<<< Önceki Konu

Sonraki Konu >>>