İstatistik derslerini tablet üzerinden çalışmanız şiddetle tavsiye olunur.
Normal Dağılım
Bu bölümde istatistiğin en önemli konularından biri olan Normal Dağılım'a (Normal Distribution) değinilecektir. Standart Normal Dağılım ile olasılık sorularının nasıl hesaplandığı anlatılacak, opsiyonel olarak IBM SPSS yazılımında ve Python programlama dilinde nasıl kullanabileceğimizi öğreneceğiz.
1733 yılında De Moivre tarafından öne sürülmüş ve 1809 yılında Gauss tarafından geliştirilmiştir. Bu nedenle Gauss Dağılımı olarak da bilinir.
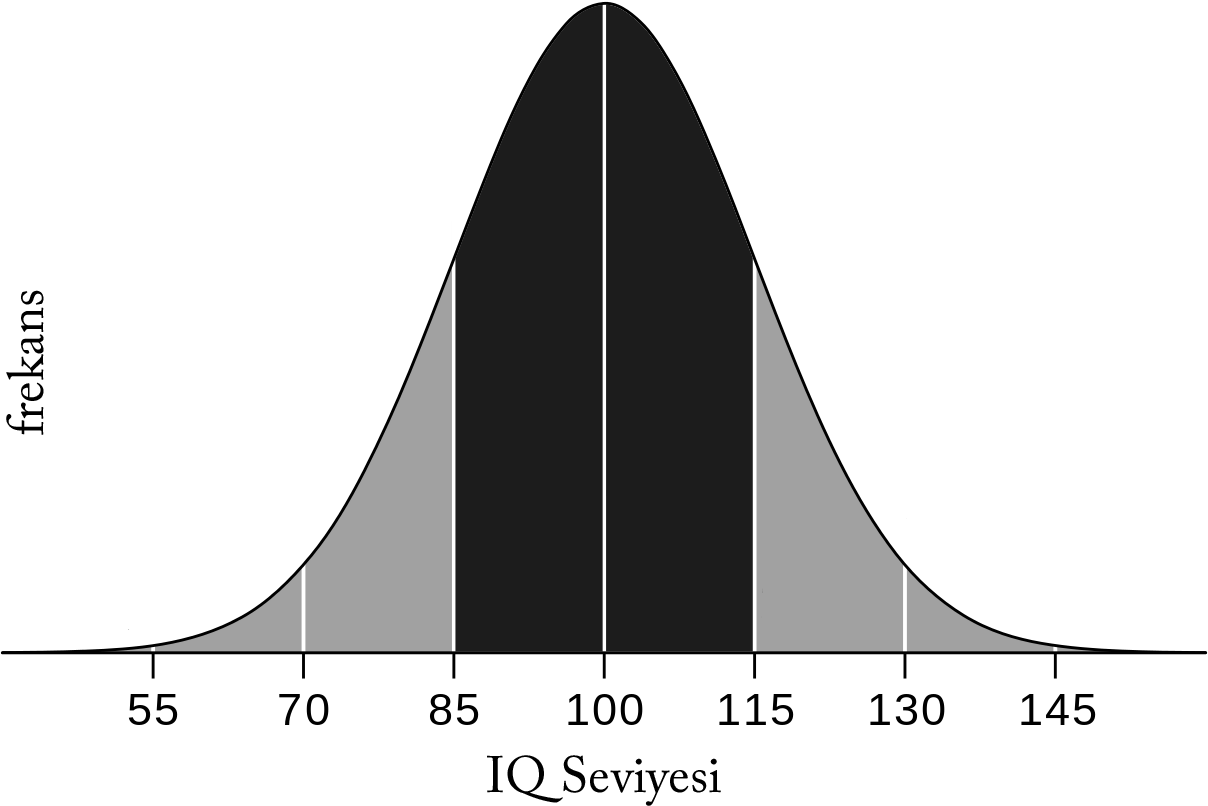
İnsanlar üzerinde yapılan araştırmalarda boy uzunluğu, zekâ seviyesi gibi değerlerin simetrik bir dağılım sergilediği gözlemlenmiş, normal dağılım bu gündelik bilgilerden türetilmiştir. Örneğin; birçok insanın zekâ seviyesi 85 ve 115 IQ arasında değişmektedir. Dağılım grafiğini oluşturduğumuzda görseldeki gibi bir grafik elde ederiz. Zekâ seviyesinin ortalaması 100'dür ve simetrik bir dağılıma sahiptir. İşte bu tür dağılımlar istatistikte normal dağılım olarak tanımlanır.
Bu dağılım grafiği bir çana benzediği için çan eğrisi olarak da adlandırılır. Özellikle üniversite öğrencilerinin sınav notlarının hesaplanması sonrası AA, BA, ... DD, FF şeklinde giden puanlamalarında sıklıkla kullanılır.
Bir önceki ders olan Olasılık Teorisi'nde olasılık yoğunluk fonksiyonlarına ve sürekli dağılımlara değinmiştik. Normal dağılım da bir sürekli dağılımdır.
olasılık yoğunluk fonksiyonudur.
Standart Normal Dağılım
Normal dağılım ile olasılık hesaplamak zordur. Bu nedenle normal dağılım fonksiyonundaki
ifadesi
Z adlı yeni bir değişkende tanımlanır. μ = 0 ve σ = 1 kabul edilir. Z değeri formüle uygulandığında
standart normal dağılım (standart normal distribution) olasılık yoğunluk fonksiyonu oluşturulur.
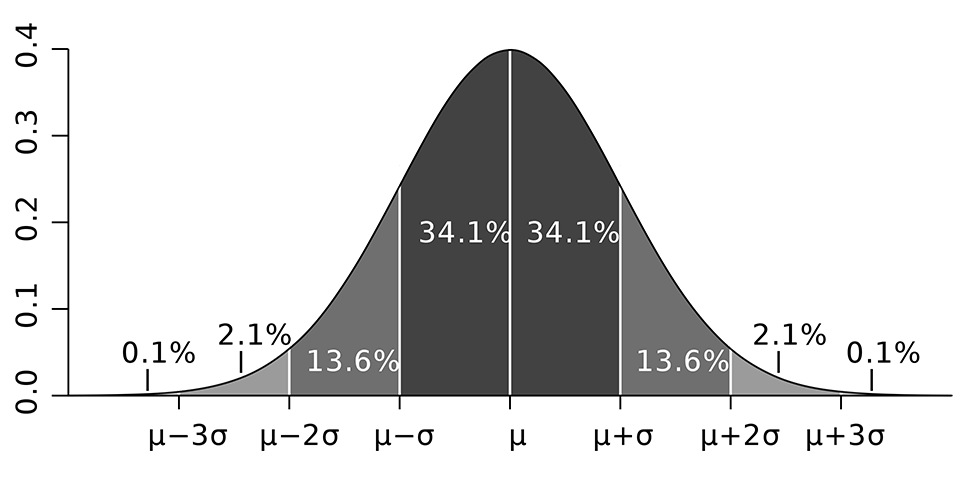
Standart normal dağılım grafiği görseldeki gibi oluşacaktır. y ekseninde yoğunluk değerleri bulunmaktadır. x ekseninde ise en ortada μ değeri yer alır. μ'nün ±1σ aralığı %34.1 + %34.1 = %68.2 olduğunu belirtir. Diğer bir ifade ile verilerin %68.2'si ortalamanın ±1σ olduğu aralıkta dağılmıştır.
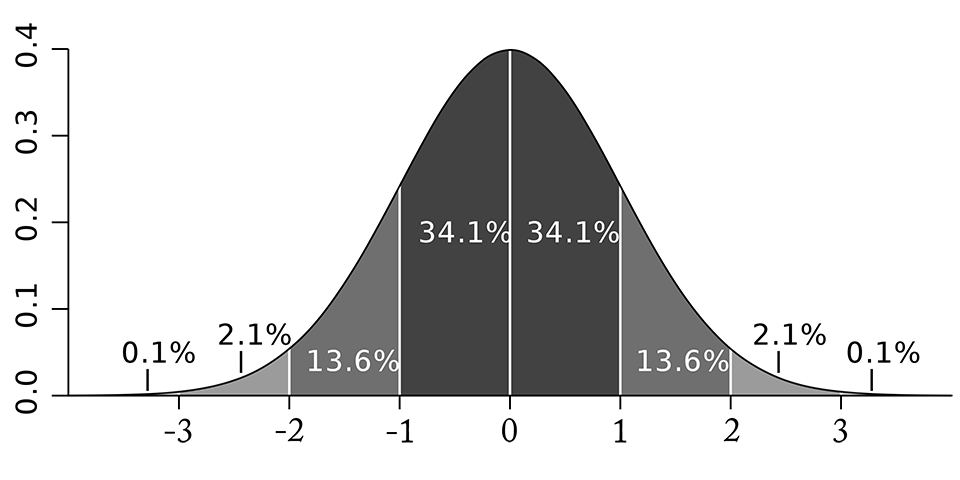
μ = 0 ve σ = 1 demiştik. Tablonun x eksenini görseldeki gibi değiştirirsek Z-Dağılımını (Standart Normal Dağılımı) elde ederiz. x eksenindeki değerler Z değerleridir.
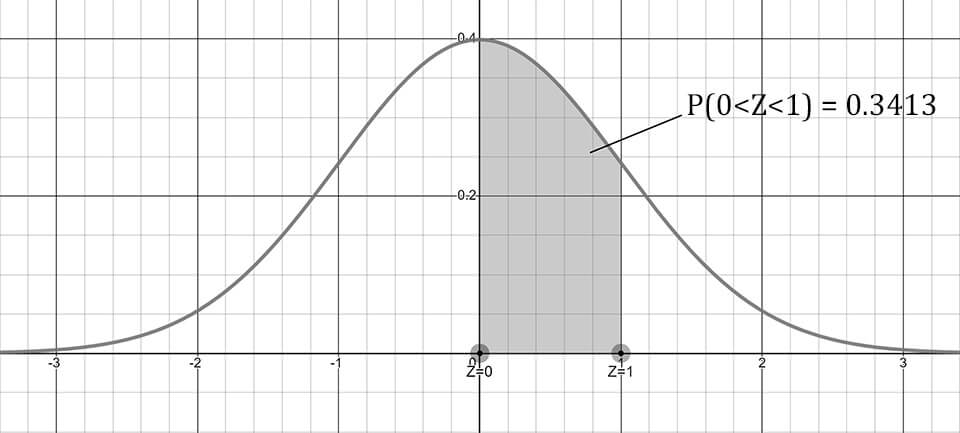
P(0 < Z < 1) = 0.3413 = %34.13'tür. Diğer bir ifade ile tüm verilerin %34.13'ü bu alandadır. Peki bu değeri kendimiz bulmak istersek ne yapmalıyız?
Bunun için z-Tablosu adı verilen standart normal dağılım tablosunu kullanmalıyız.
Standart Normal Dağılım Tablosu (z-Tablosu)
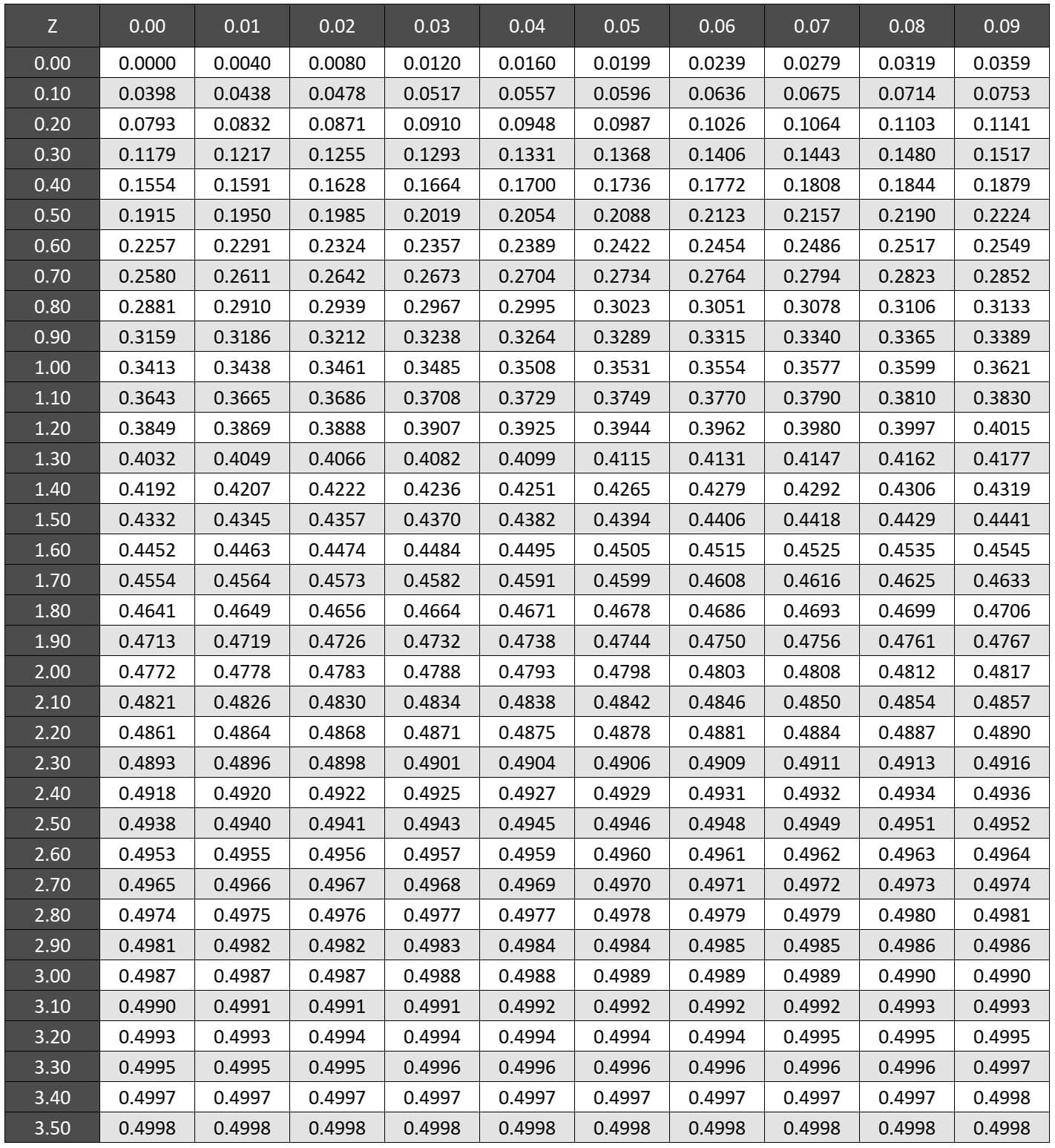
Her istatistikçinin elinin altında olan bir tablodur. Standart normal dağılım sorularında Z değeri bilinen olasılıkları bulmak için kullanılır.
z-Tablosu için yukarıdaki bağlantıya tıklayabilir ve PDF formatında indirebilirsiniz. Renk ve font düzenlemeleri yapmak isterseniz bu bağlantıya tıklayabilir, Excel formatında indirebilirsiniz.
Şimdi gelelim sorumuza. P(0 < Z < 1) aralığındaki olasılığı nasıl 0.3413 bulduğumuzu hesaplıyorduk.
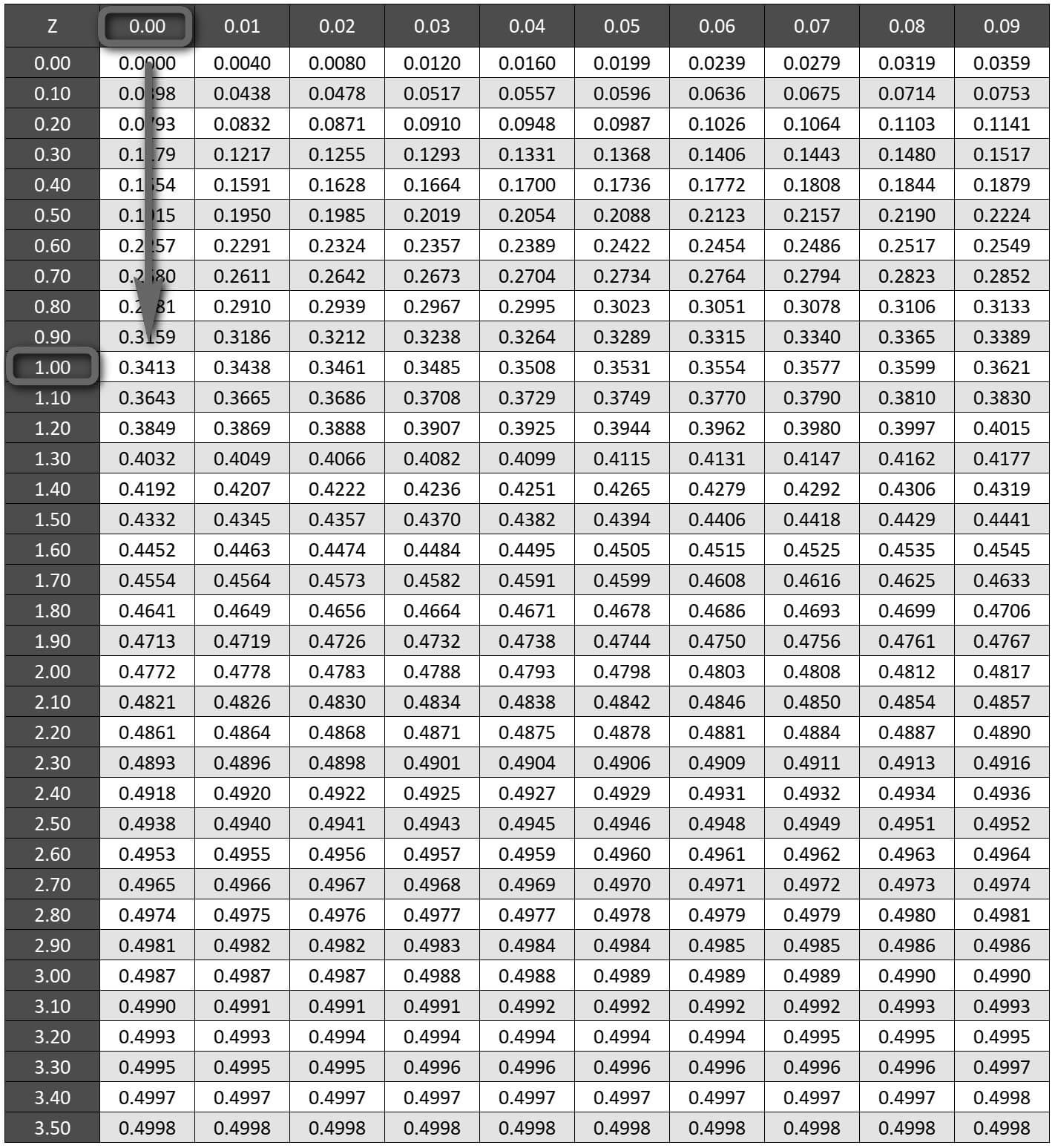
Bu olasılık z-Tablosundaki 1.00 ve 0.00 alanlarına denk gelen hücredir. Bu da 0.3413 değeridir. Şimdi farklı örnekler yapalım. Konuyu birazdan tam olarak anlayacaksınız.
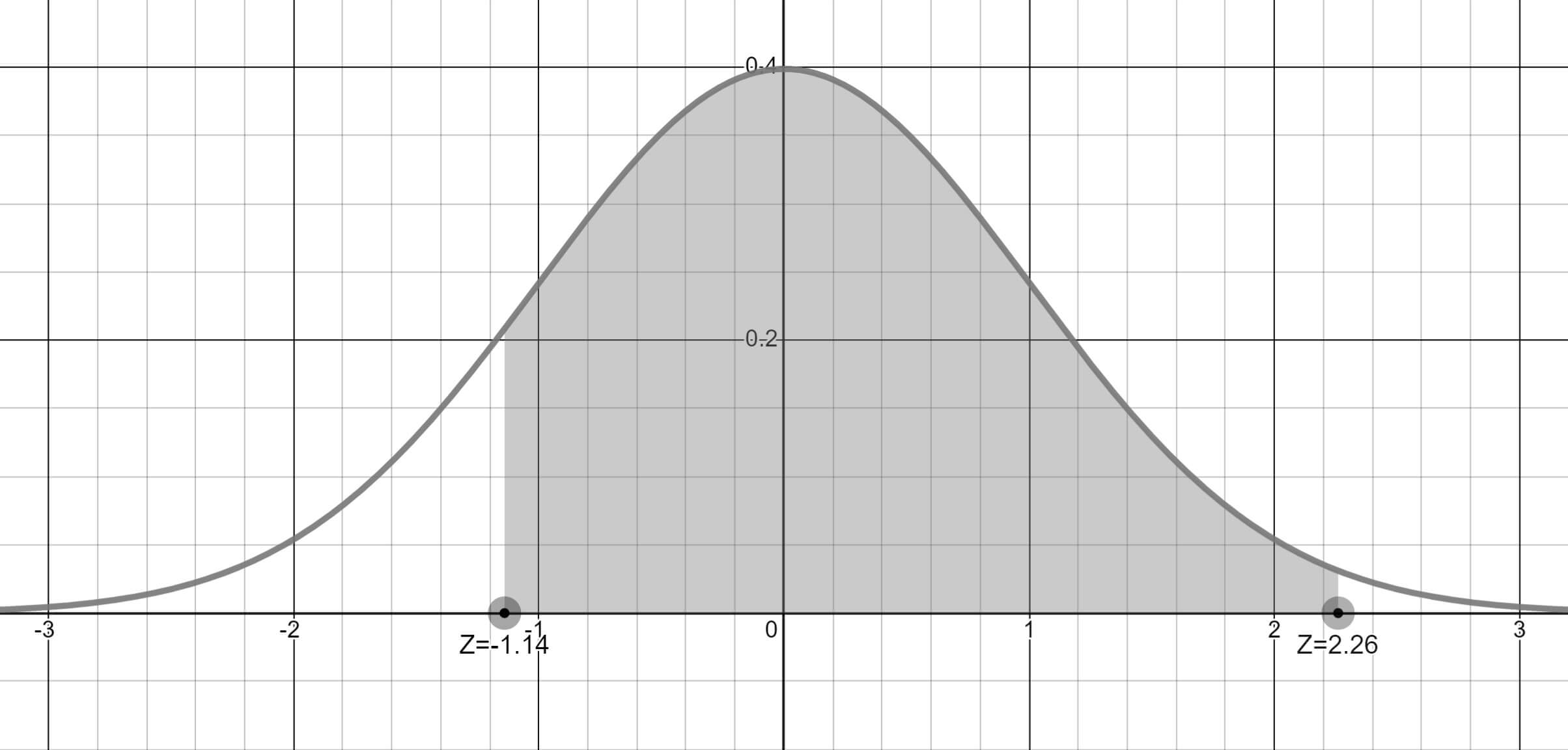
P(-1.14 < Z < 2.26) aralığındaki olasılık nedir?
Bu fonksiyonu ikiye bölebiliriz:
Simetri özelliğinden dolayı
diyebiliriz.
Özetle
fonksiyonu bu şekilde değiştirebiliriz. z-Tablosunda 1.14 ve 2.26 değerlerine bakalım.
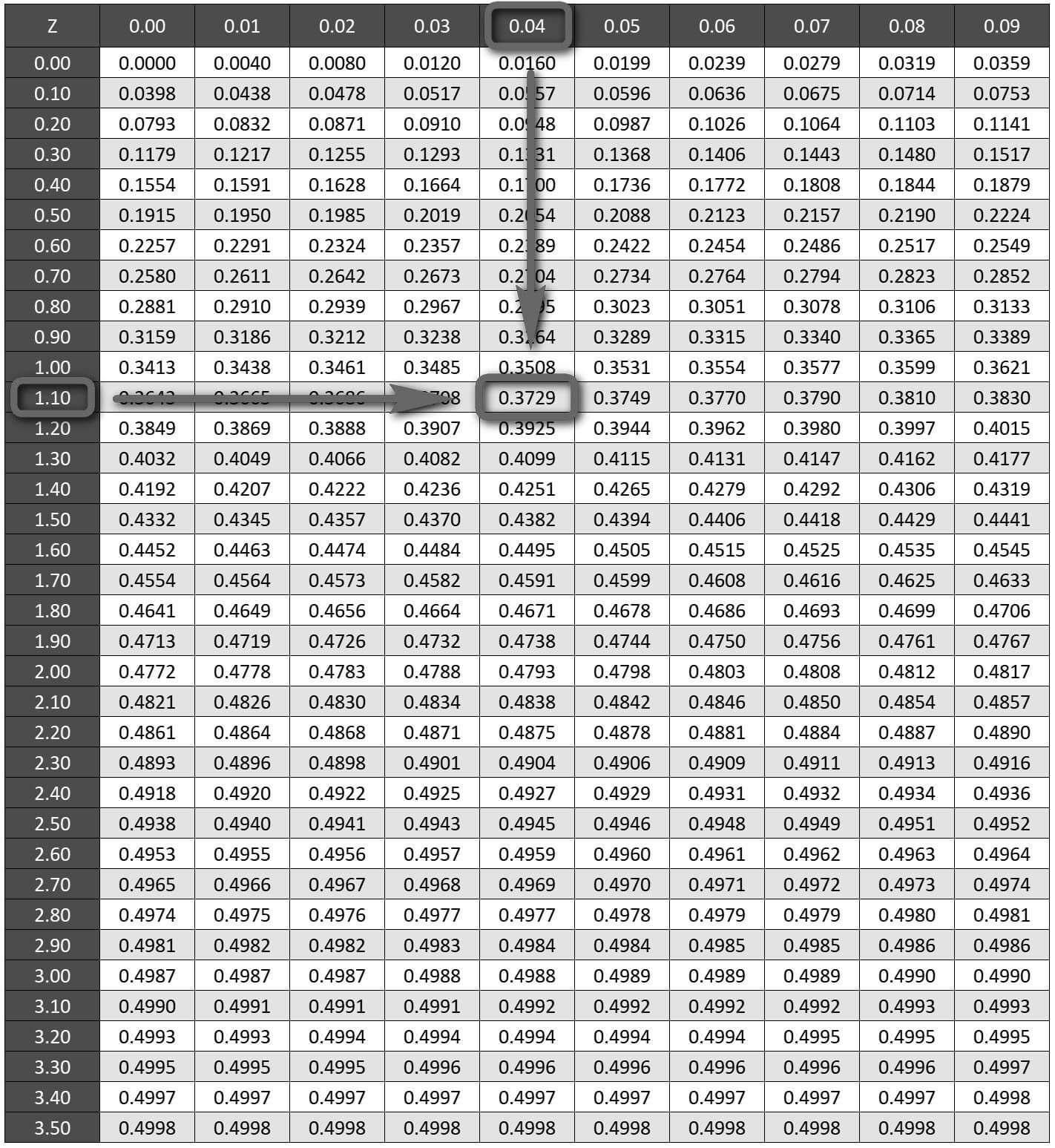
1.14 değerini bulmak için 1.14'ün ilk basamağını ve ondalığını 1.10 olarak tablodan aratırız. İkinci ondalık olan 4'ü ise sütunlardaki 0.04 başlığında aratırız. Satır değeri olan 1.10 ile sütun değeri olan 0.04'ün kesiştiği hücre bize olasılığı verecektir. Bu da 0.3729 yapar.
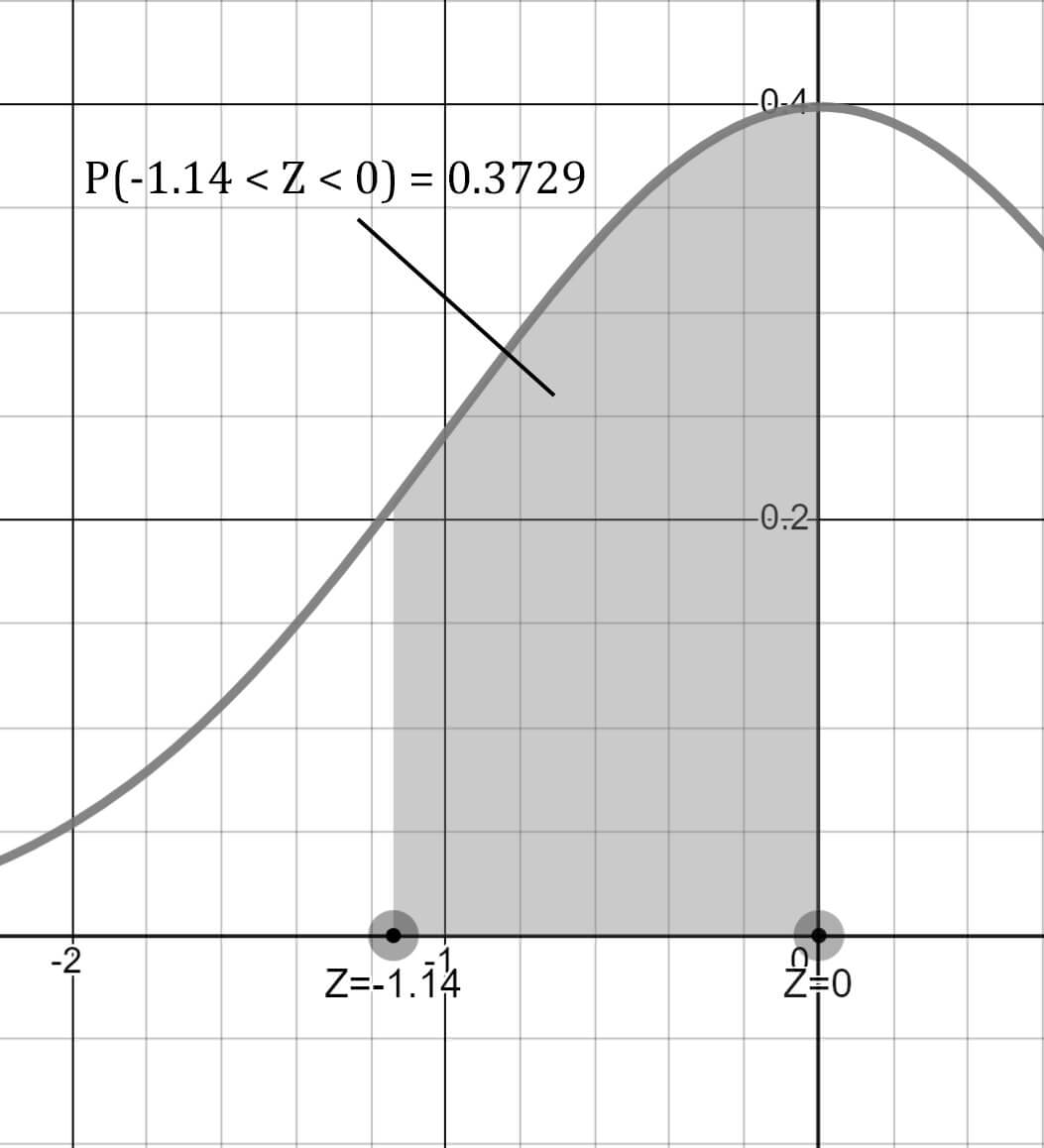
Grafiksel gösterimi yukarıdaki gibidir.
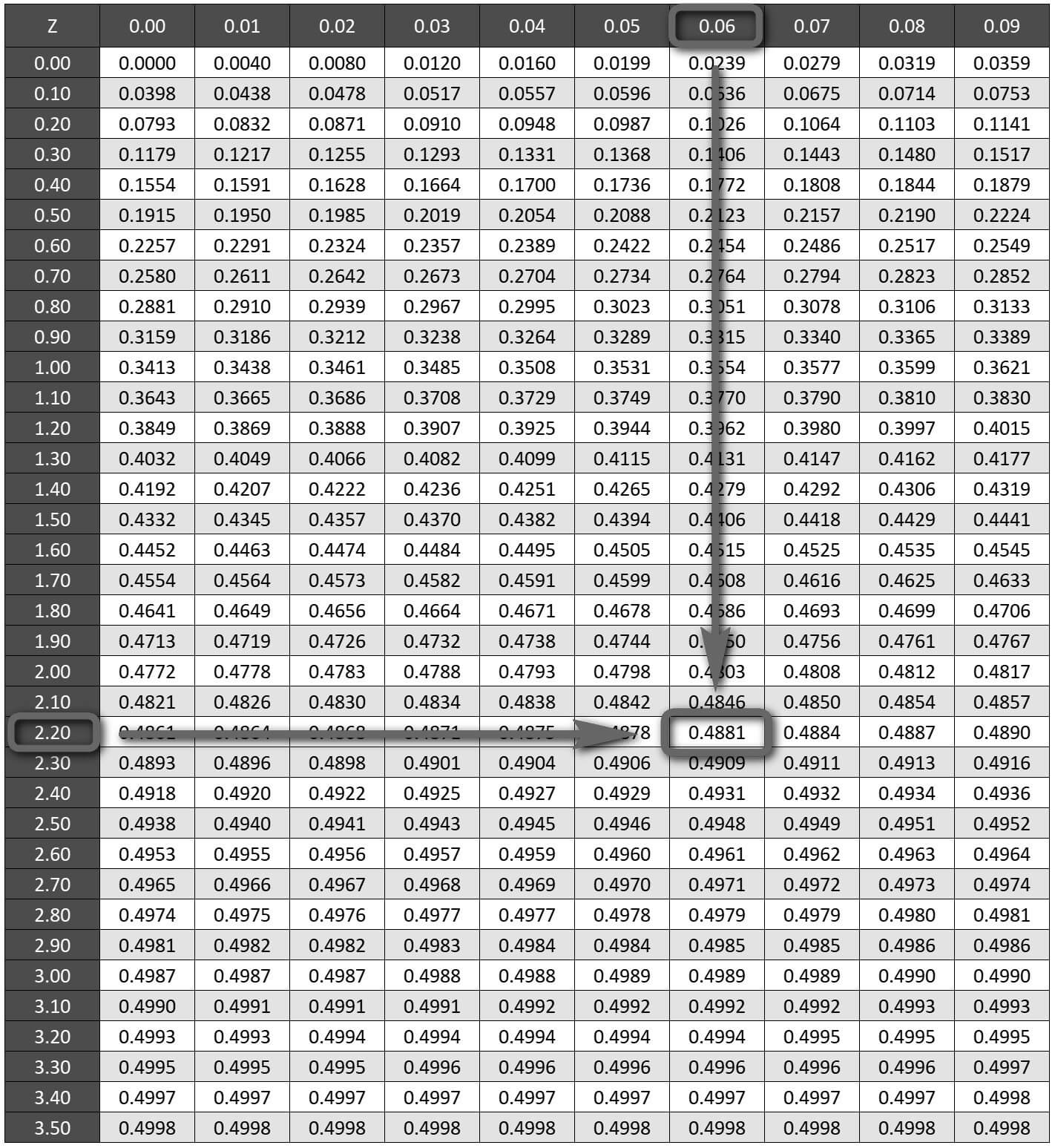
Benzer şekilde 2.26 Z değerini z-Tablosunda 2.20 ve 0.06 değerlerinin kesiştiği hücrede ararız. Bu değer 0.4881'dir.
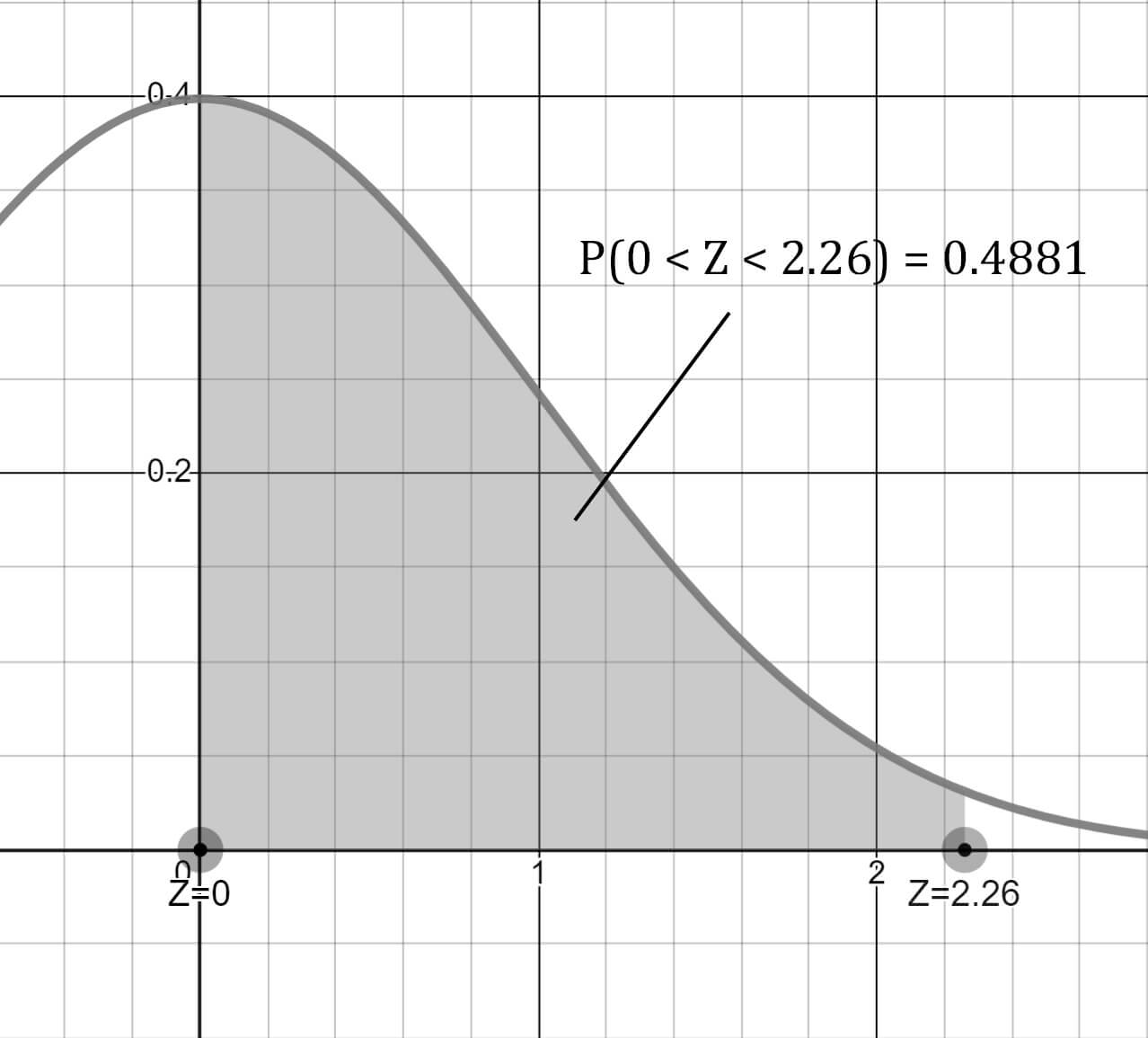
Grafiği yukarıdaki gibi oluşur.
Sonuç olarak P(-1.14 < Z < 2.26) aralığındaki olasılık %86.10'dur.
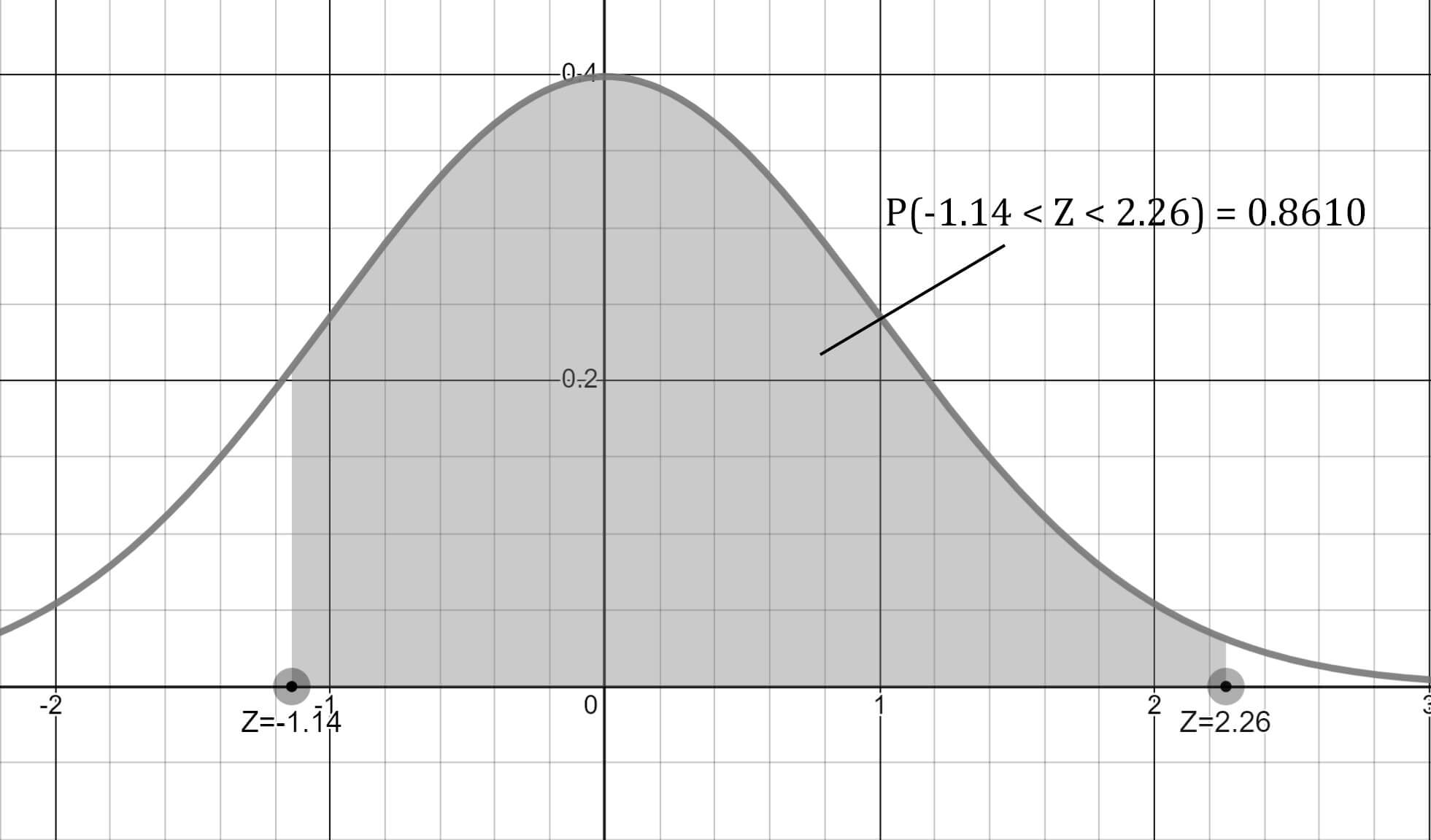
Daha önce oluşturduğumuz iki grafiği birleştirdiğimizde
P(-1.14 < Z < 2.26) aralığının normal dağılım grafiği ve olasılığı görseldeki gibi oluşacaktır.
Evet hepsi bu kadar. Tablo ve grafik okumayı anladıysanız standart normal dağılımı da anlamışsınızdır.
Bazı noktalara değinmekte fayda var:
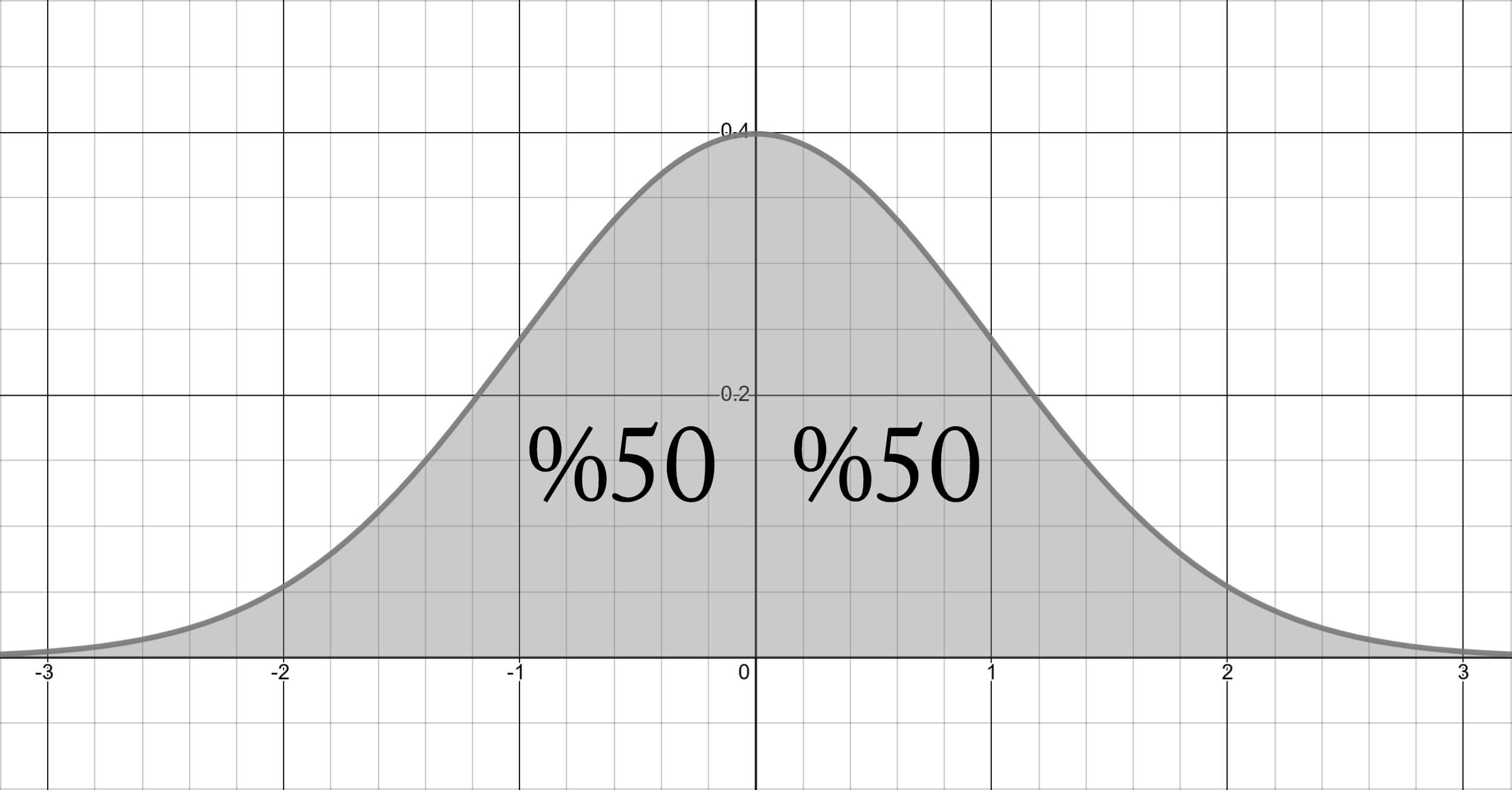
P(Z < 2.37) değeri aslında P(0 < Z < 2.37) + %50 ile aynı anlama gelmektedir. Standart normal dağılım simetrik olduğu için sol ve sağ tarafı, 0'dan aşağısı ve yukarısı, her bir alan %50 olasılığa sahiptir. Birçok soruyu sol ve sağ tarafınının %50 olasılığa sahip olmasıyla hesaplayacağız.
P(Z > 1.44) değeri simetri özelliğinden dolayı %50'den P(0 < Z < 1.44) olasılığını çıkardığımızda hesaplanabilecektir.
Kafanız karışmış olabilir. Hiç merak etmeyin. Standart normal dağılımı soru çözdükçe çok daha net anlayacaksınız. Şimdi gerçek bir örnek yapalım:
Standart Normal Dağılım Örneği
Bir okuldaki öğrencilerin boy uzunlukları hesaplanmış ve boy uzunluklarının normal dağılım sergilediği gözlemlenmiştir. Boy uzunluklarının ortalaması 176 cm, standart sapması 14 cm'dir. Buna göre
- 170 cm'den kısa öğrenci olma olasılığı kaçtır?
- 180 - 190 cm aralığında öğrenci olma olasılığı kaçtır?
- 160 cm'den uzun öğrenci olma olasılığı kaçtır?
- 160 cm'den kısa, 190 cm'den uzun öğrenci olma olasılığı kaçtır?
Yanıt 1 - 170 cm'den kısa öğrenci olma olasılığını bulmadan önce bize verilen normal dağılımı standart normal dağılıma çevirelim.
demiştik. Buna göre
Z değerimiz -0.4286'dır. Yuvarlama ile -0.43 diyebiliriz.
Burada bir duralım ve grafiğimize bakalım.
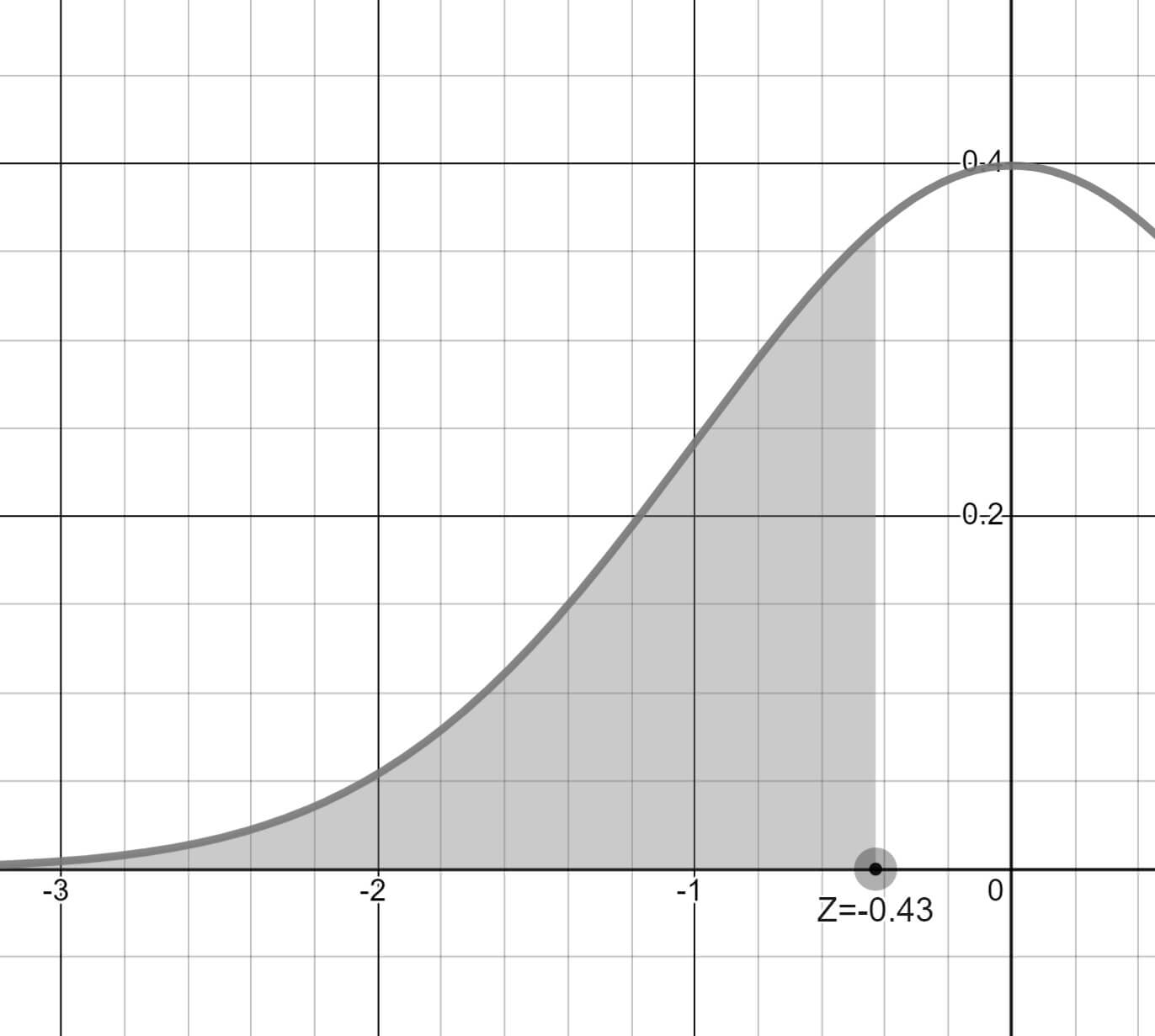
-0.43 altındaki alanı arıyoruz değil mi? 170 cm'den kısa öğrencileri.
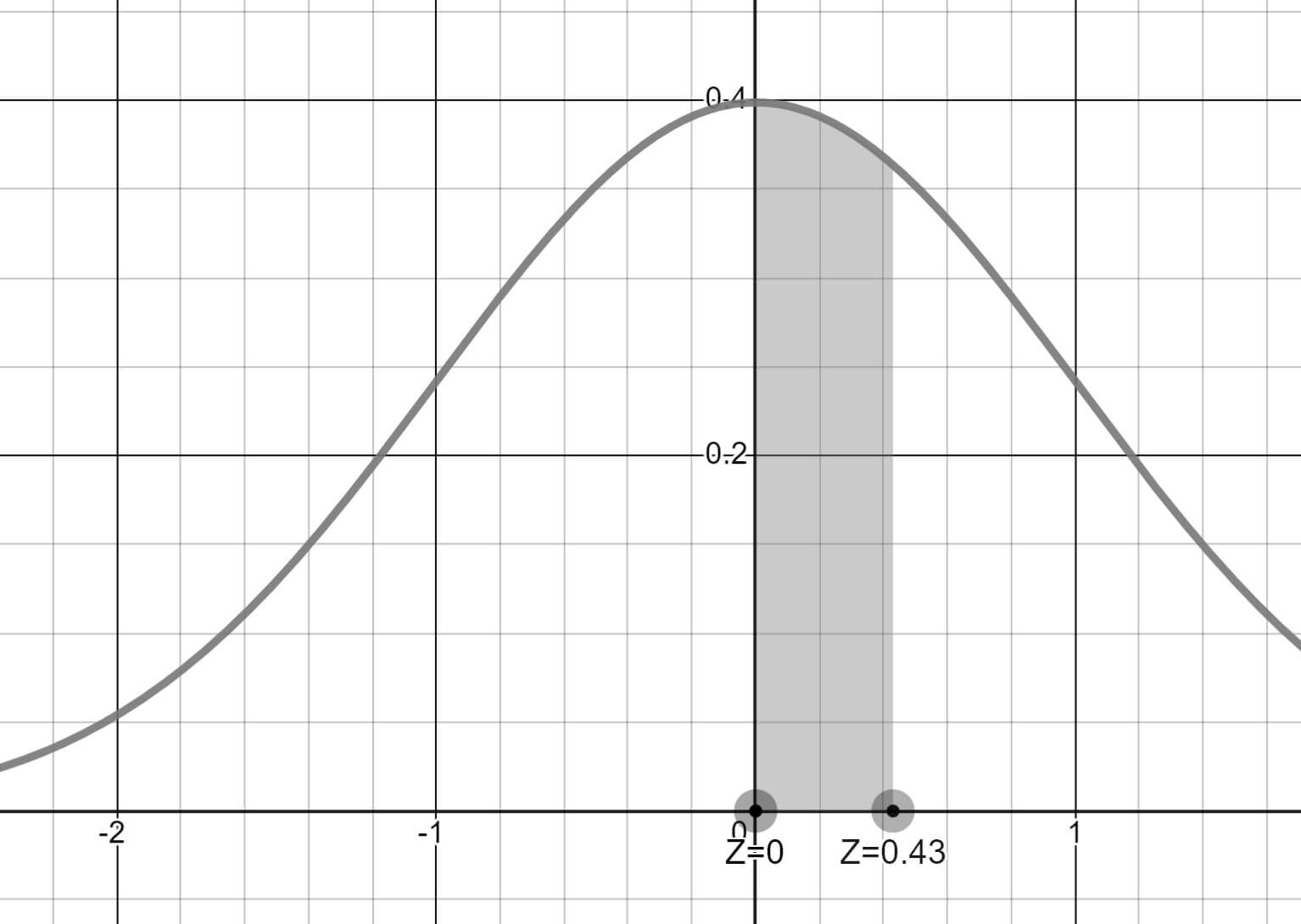
Simetri özelliğinden faydalanıp önce P(Z < 0.43) alanındaki olasılığı bulabiliriz.
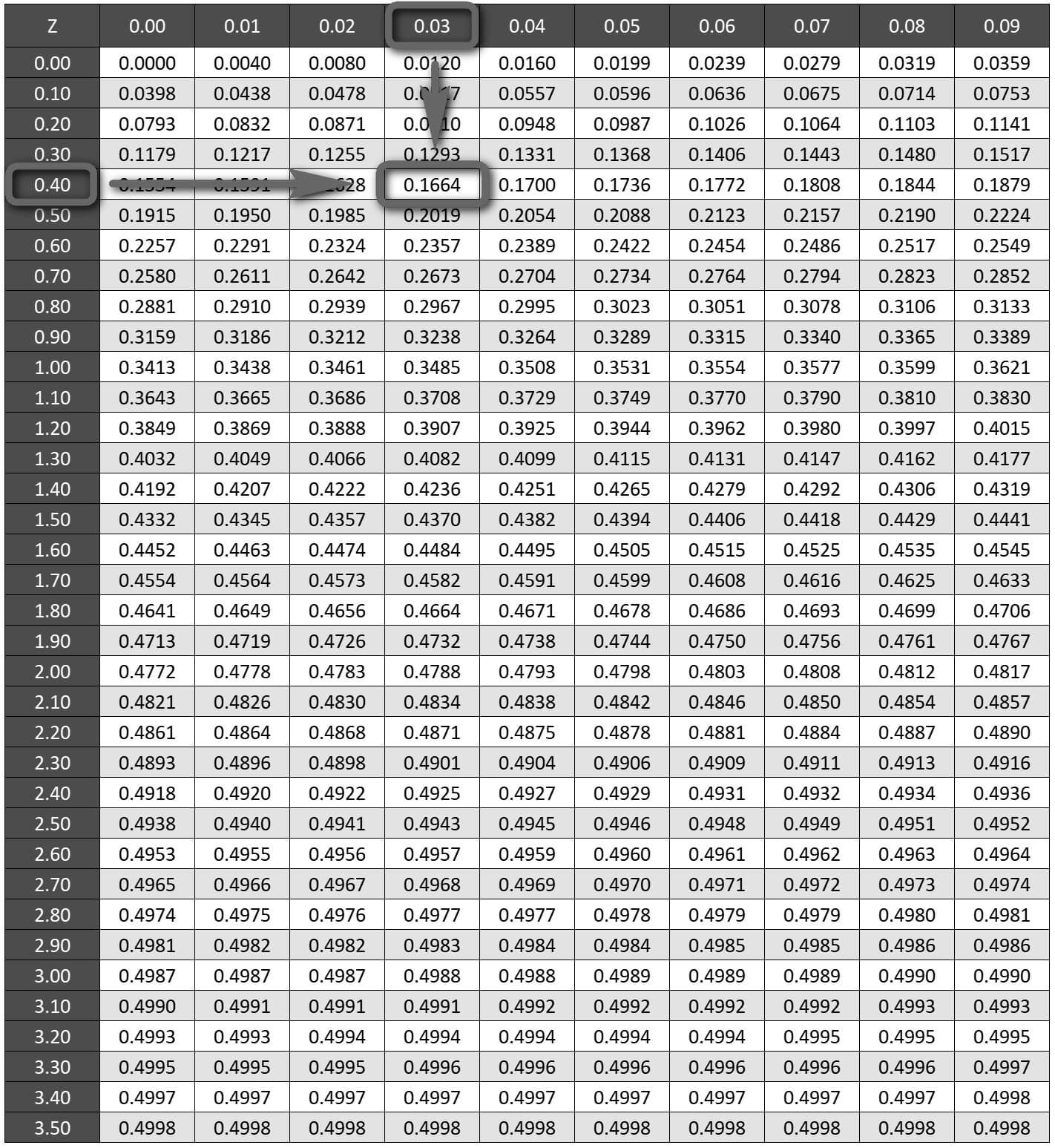
z-Tablosunda 0.43 değeri 0.40 ve 0.03 Z değerlerinin kesiştiği hücre olan 0.1664 değeridir.
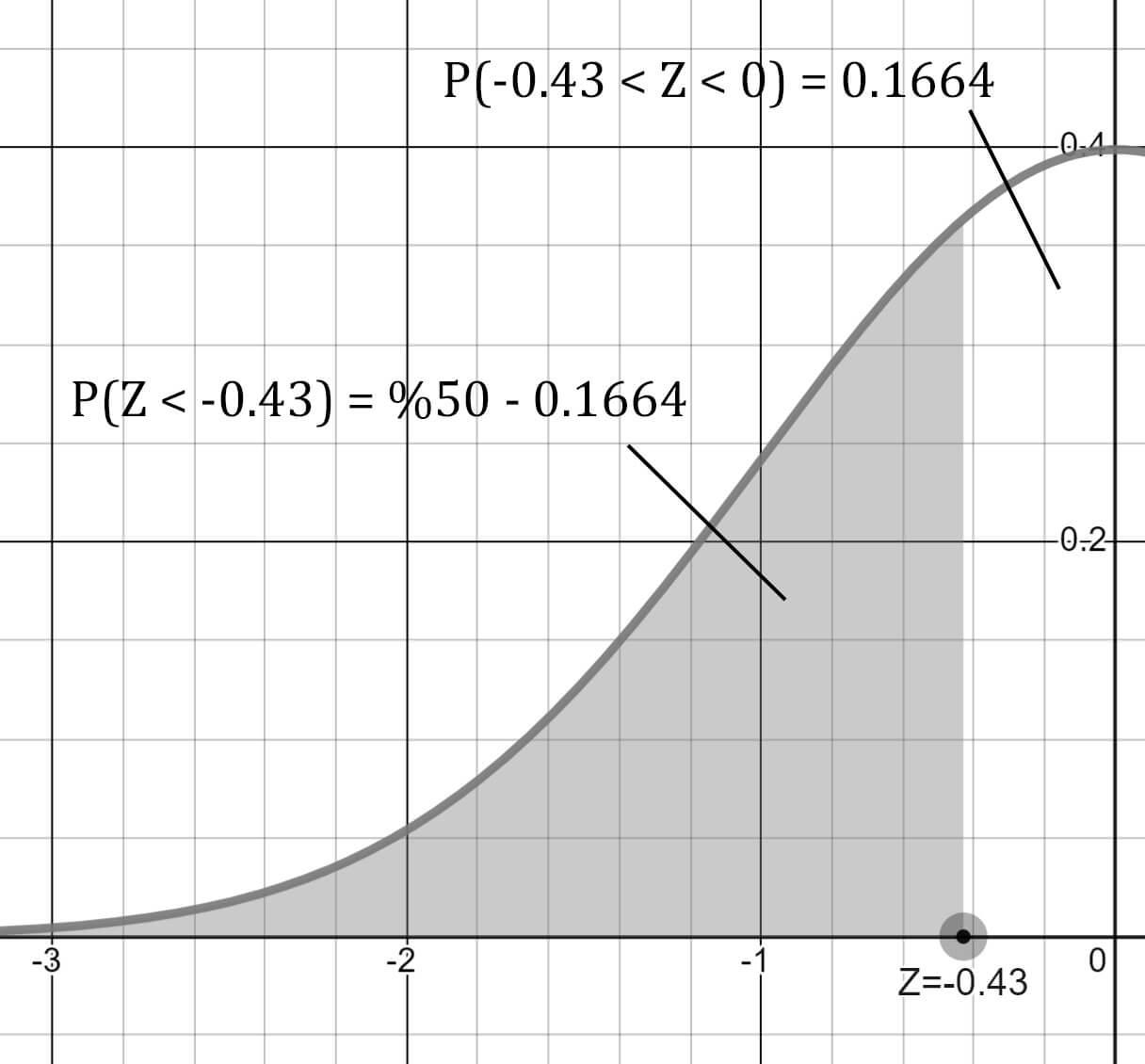
Dağılım sol tarafı %50 olasılığa sahip ise
%50'lik dilimden dahil etmek istemediğimiz %16.64'lük dilimi çıkardığımızda 170 cm'den kısa öğrenci olma olasılığını %33.36 buluruz.
Yanıt 2 - 180 - 190 cm aralığında öğrenci olma olasılığını hesaplayalım.
Önce 180 ve 190 cm uzunlukları Z değerlerine dönüştürüz.
0.29 ve 1.00 Z değerleri arasında kalan alanı hesaplayacağız.
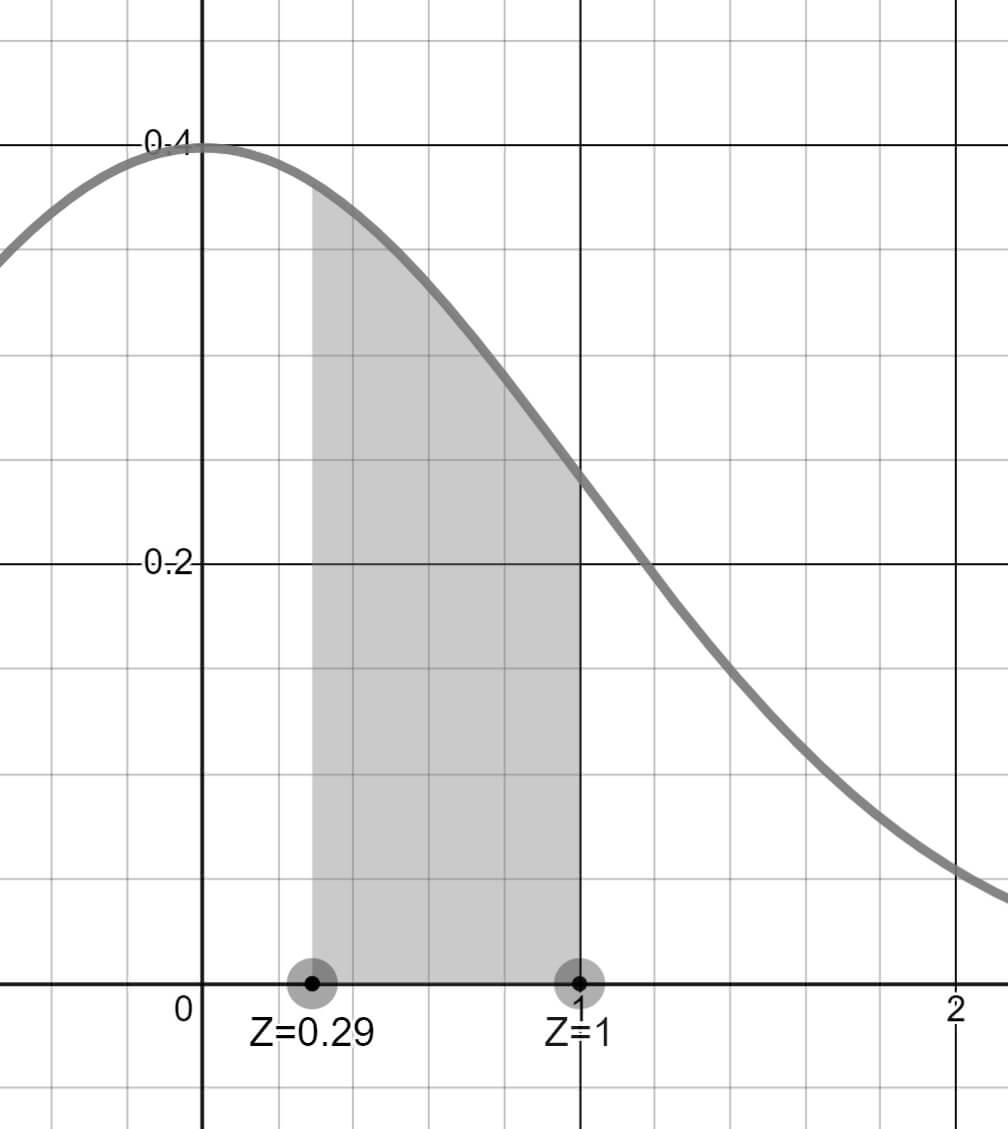
Dağılımı grafiğe döktüğümüzde istenen aralık görseldeki gibi olacaktır.
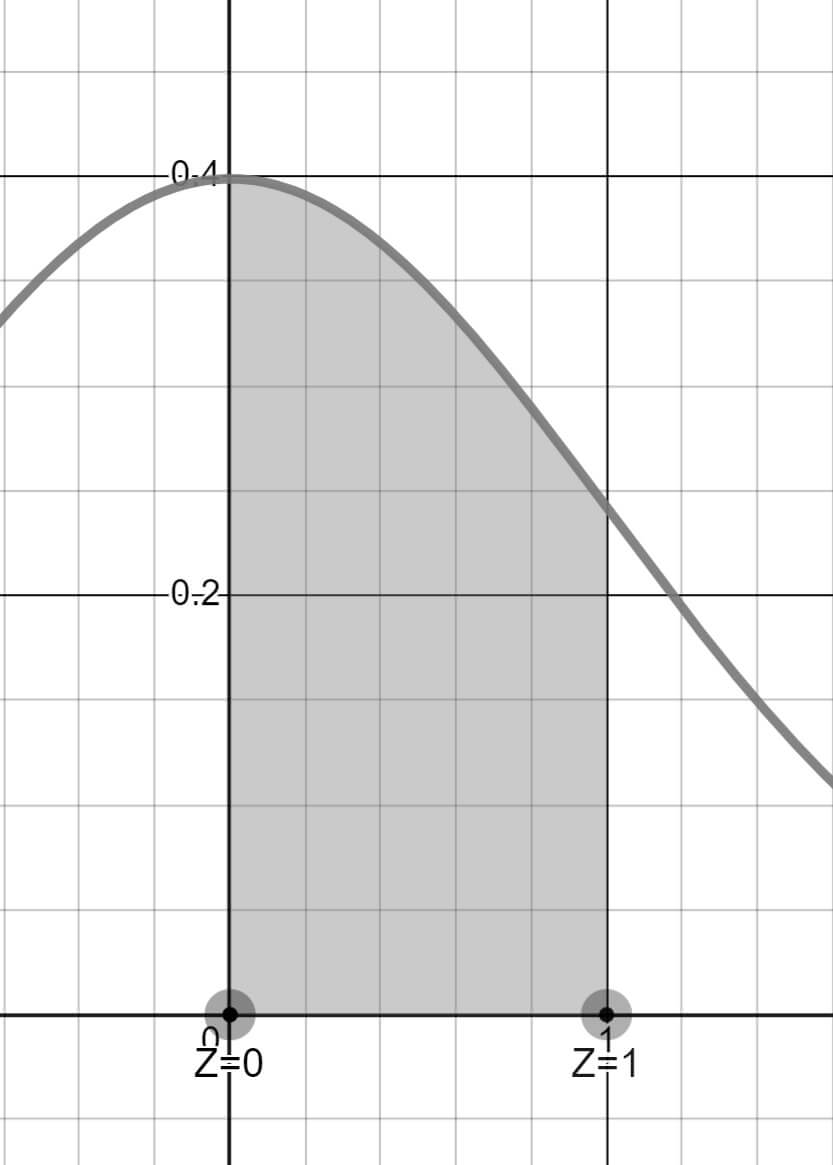
O zaman P(0 < Z < 1.00) aralığındaki alandan
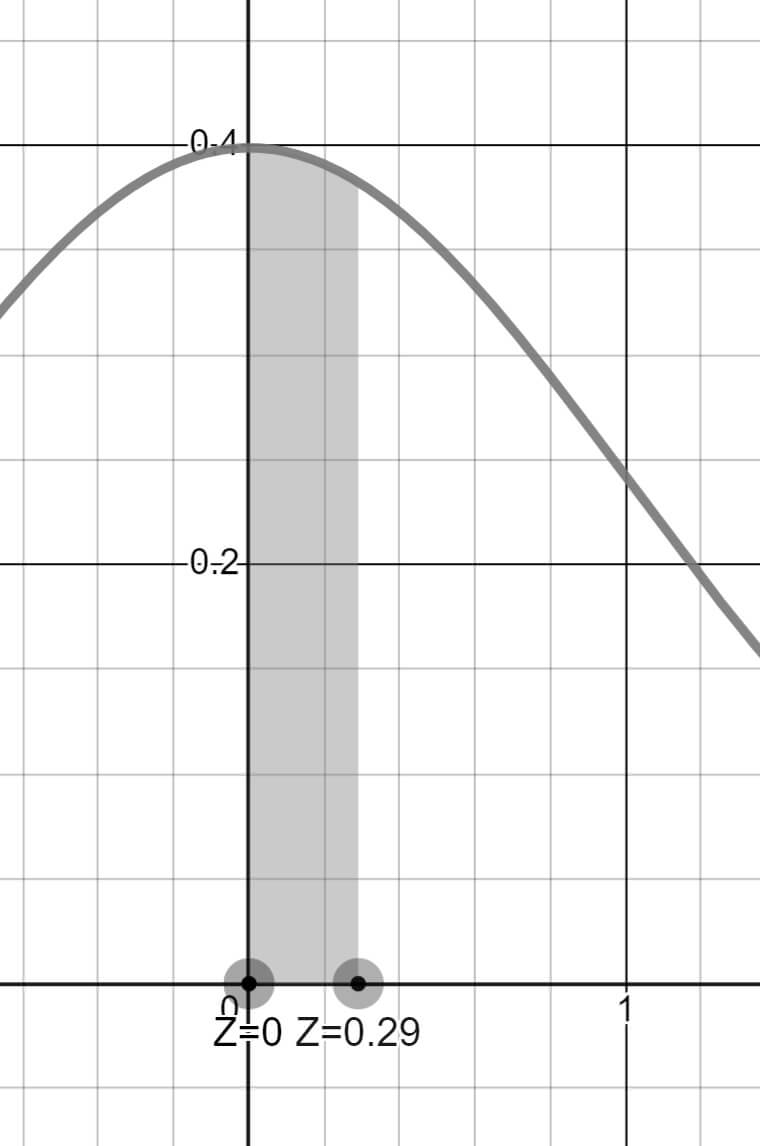
P(0 < Z < 0.29) aralığındaki alanı çıkarırsak aynı sonucu elde edebiliriz.
olasılığını hesaplamalıyız.
Z-Tablosundan bu değerleri bulur ve
180 - 190 cm boy aralığında öğrenci olma olasılığı %22.72'dir diyebiliriz.
Yanıt 3 - 160 cm'den uzun öğrenci olma olasılığını hesaplayalım.
Z değerini -1.14 buluruz.
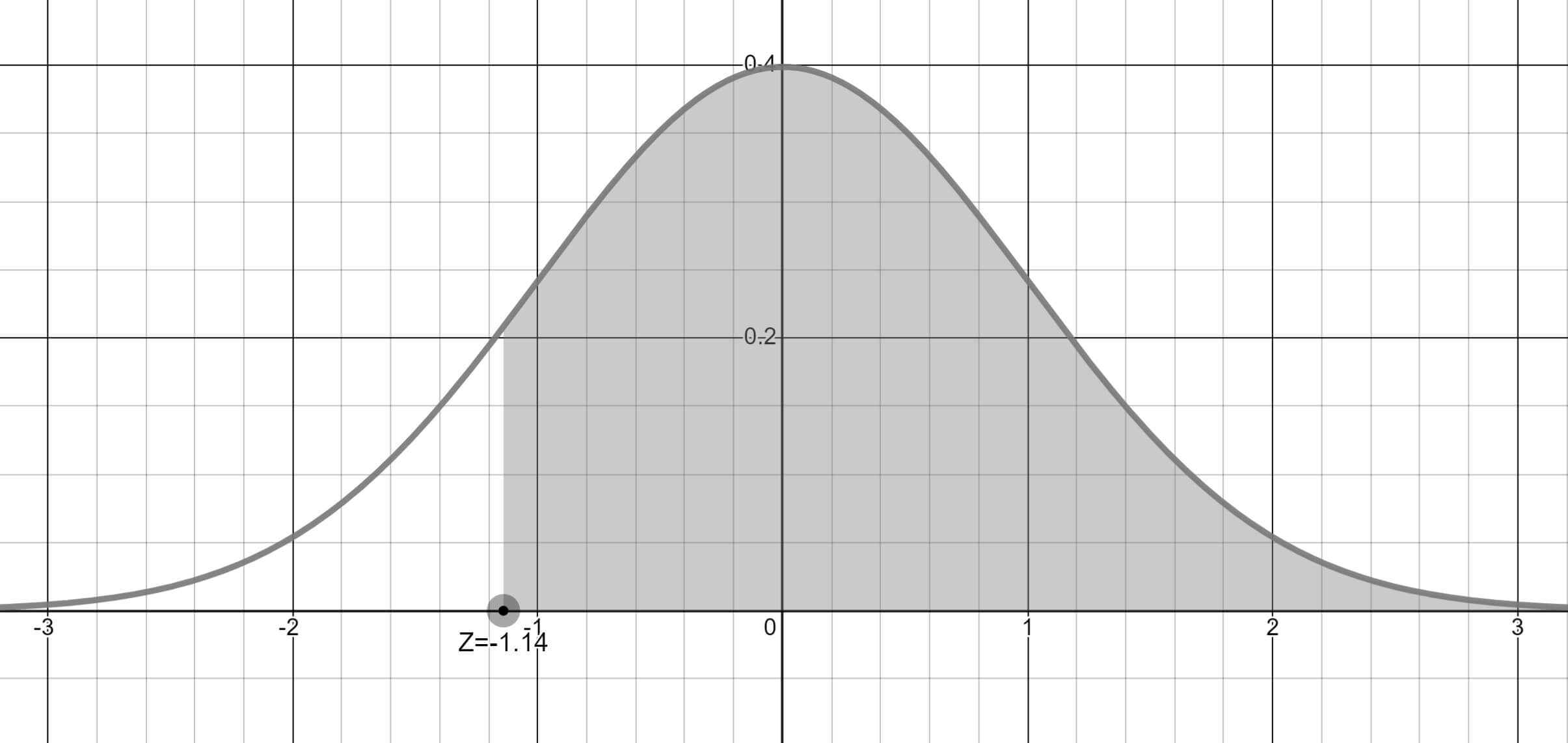
160 cm'den uzun öğrenciler sorulduğu için bu alanı arıyoruz. 160 cm'den kısa öğrenciler sorulsaydı -1.14 değerinin altında kalan alanı hesaplamamız yeterli olurdu.
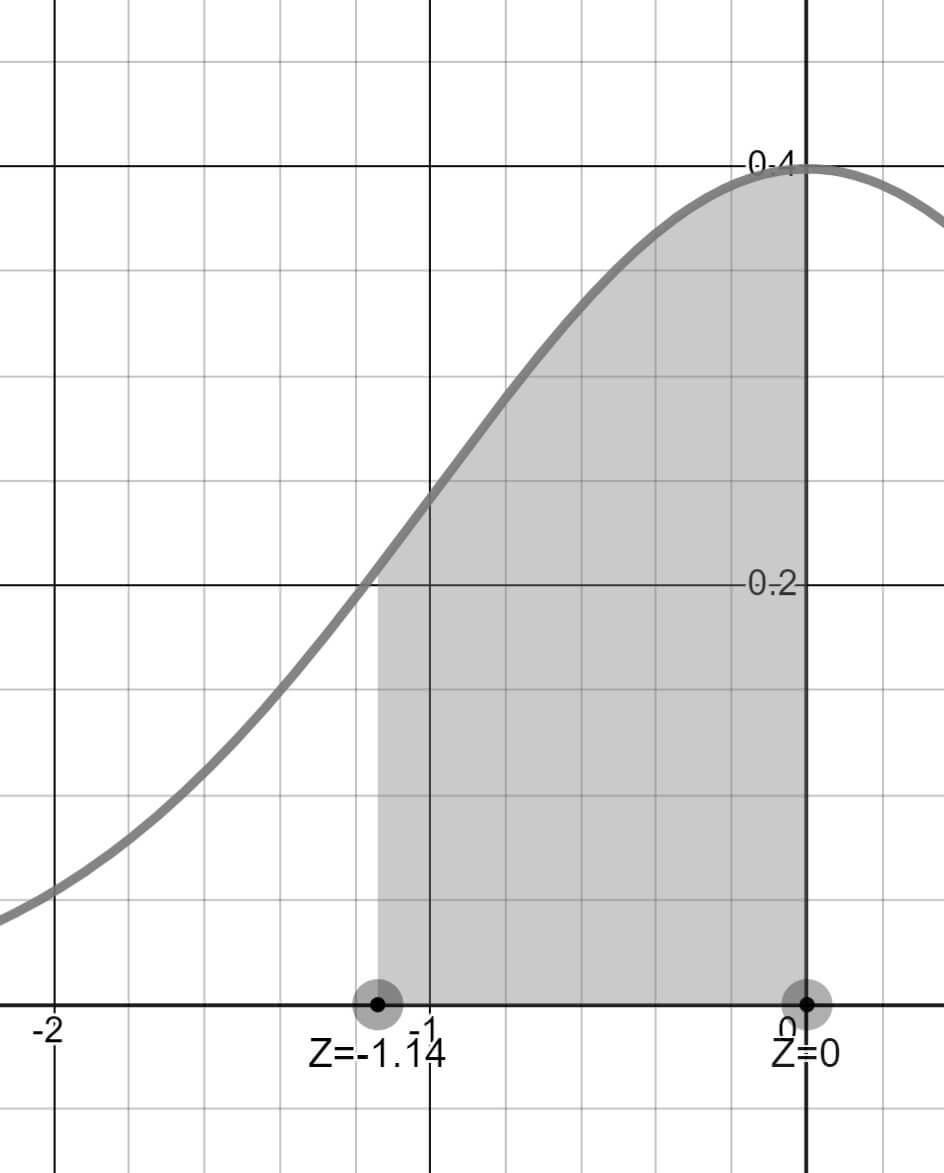
Simetri özelliği ile öncelikle P(-1.14 < Z < 0) aralığını bulalım.
z-Tablosundan 1.10 ve 0.04 Z değerlerinin kesiştiği hücreyi aradığımızda P(-1.14 < Z < 0) alanının %37.29 olduğunu buluruz.
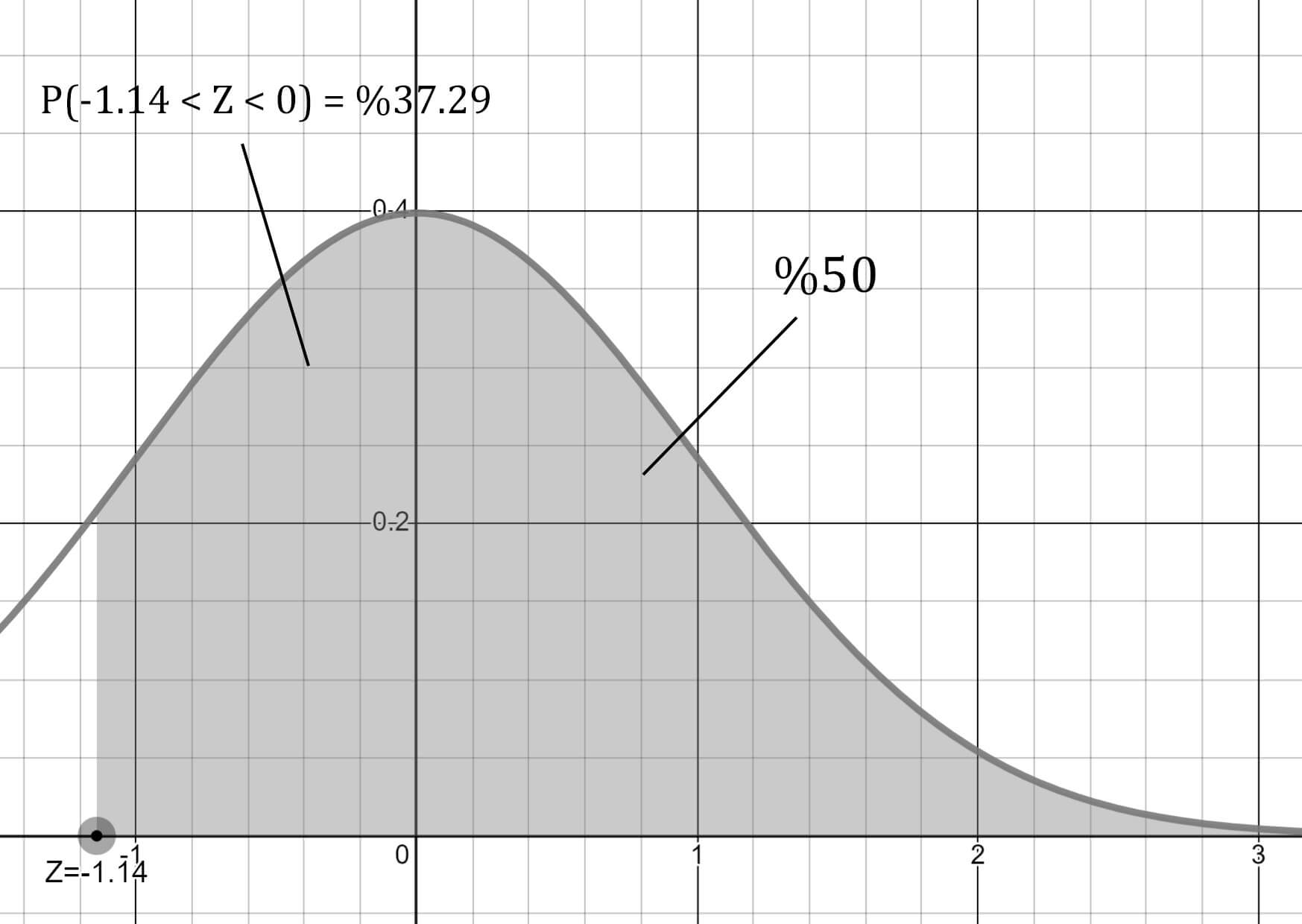
O zaman P(Z > -1.14) aralığı, diğer bir ifade ile 160 cm'den uzun öğrenci olma olasılığı %37.29 + %50'den %87.29'dur sonucuna varabiliriz.
Yanıt 4 - 160 cm'den kısa, 190 cm'den uzun öğrenci olma olasılığını hesaplayacağız.
Öncelikle Z değerlerimizi hesaplayalım.
160 cm'den kısa olma olasığını P(Z < -1.14) olasılığında hesaplayacağız.
190 cm'den uzun olma olasılığını ise P(Z > 1.00) olasılığında hesaplayacağız.
Soruda
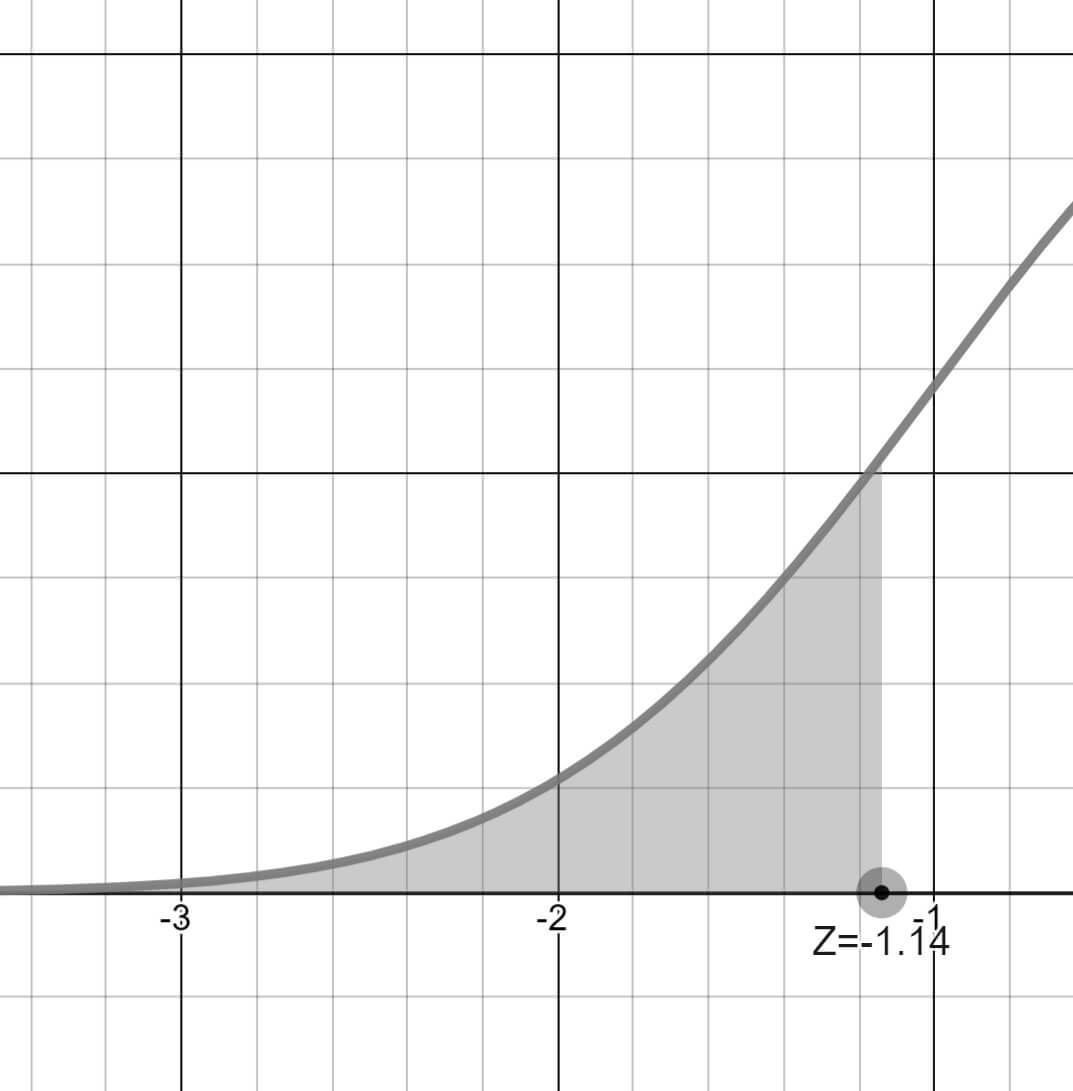
dağılımın sol tarafındaki alan ile
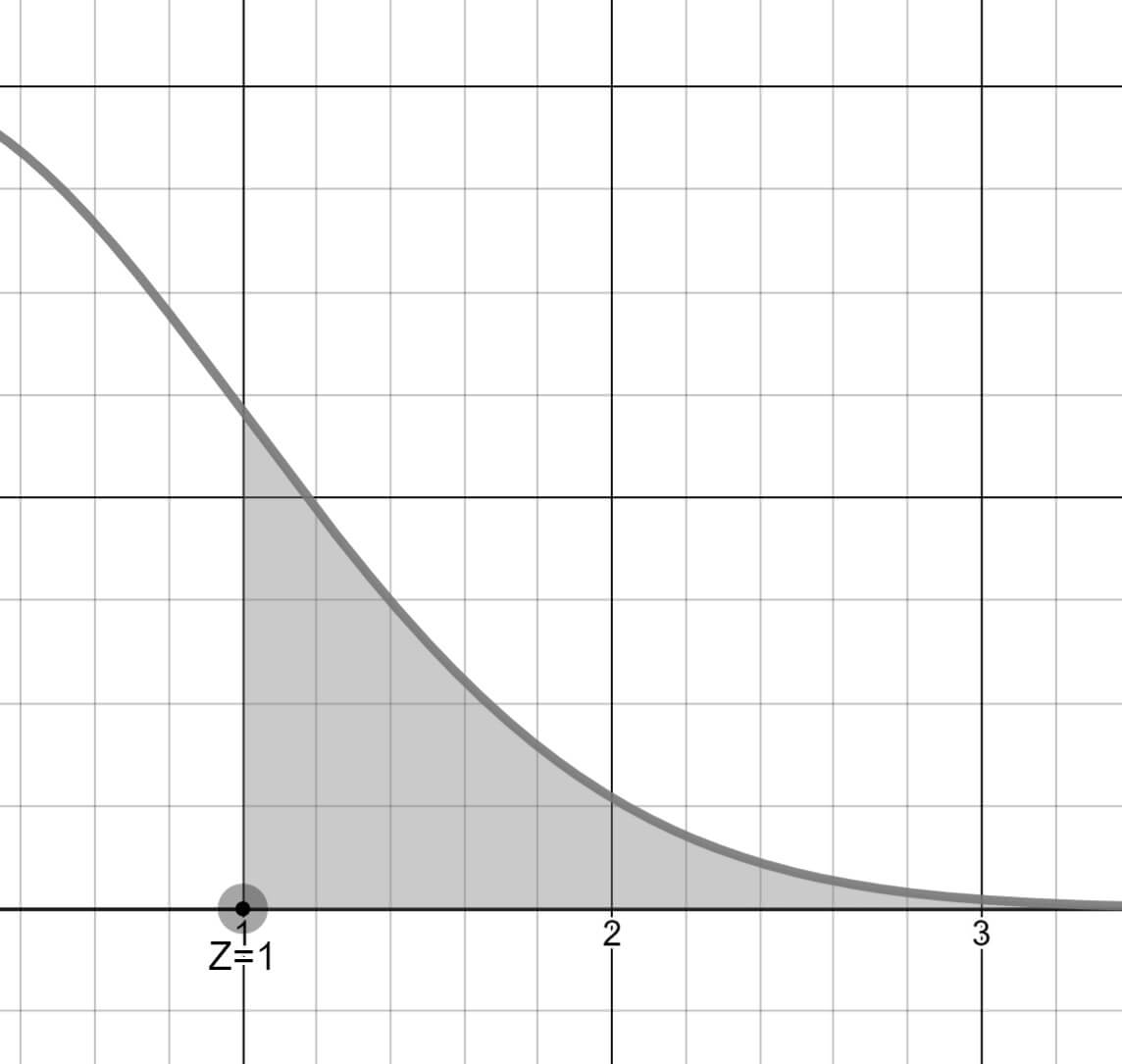
sağ tarafındaki alanın toplamı soruluyor.

Daha önce bu aralığa ait olasılığın %37.29 olduğunu bulmuştuk.

O zaman sol taraftaki alanın olasılığı %50'den daha önce bulduğumuz aralığın olasılığı olan %37.29'u çıkarırsak 160 cm'den kısa öğrenci olma olasılığını %12.71 buluruz. Şimdi 190 cm'den uzun olma olasılığına bakalım.

Yine daha önce bu aralığın %34.13 olduğunu bulmuştuk.

Bu şekilde dağılımın sağ tarafında kalan aralığın %50 - %34.13'ten %15.87 olduğunu söyleyebiliriz. 190 cm'den uzun olma olasılığını da bulduk.
Soruda hem 160 cm'den kısa olanlar hem de 190 cm'den uzun olanlar sorulduğu için %12.71 + %15.87'den yanıtın %28.58 olduğunu söyleyebiliriz.
Görüldüğü gibi z-Tablosu ile olasılık hesaplaması bu kadar kolay.
Kimi kaynaklarda sorunun sonunda N(0,1) yazmaktadır. 0 burada ortalamayı, 1 ise standart sapmayı belirtir. Diğer bir ifade ile soruda standart normal dağılım kullanıldığı belirtilir. Bu nedenle soruların sonunda N(0,1) ifadesini görürseniz bilinki standart normal dağılım
(z-Dağılımı) kullanmanız istenmektedir.
Casio fx-991EX ile Normal Dağılım
Casio fx-991EX bilimsel hesap makinesi ile standart normal dağılımı hesaplaması oldukça kolaydır.

Biraz önceki örneğimizde "170 cm'den kısa öğrenci olma olasılığı kaçtır?" sorusunu yanıtlamıştık. Standart normal dağılımda
P(Z < -0.43) alanının olasılığını hesaplamak istemiştik.

İlk olarak hesap makinemizi açalım ve Menu tuşuna basalım. Çıkan listeden normal dağılımı seçmek için 7 tuşunu seçelim.

Standart normal dağılım hesaplaması yaptığımız için 2:Normal CD seçimini yapmalıyız. Bunun için 2 tuşuna basalım.

P(Z < -0.43) olasılığı aslında P(-5.00 < Z < -0.43) aralığındadır. Yani eğrinin sol tarafı minimum -5.00 iken sağ tarafı +5.00'dir. Bu nedenle Lower değeri için -5 yazalım ve Eşittir tuşuna basalım. Upper değeri için -0.43 yazalım. Eşittir tuşu ile bir alta geçebiliriz. Standart normal dağılım kullandığımız için σ (standart sapma) 1, μ (ortalama) 0 değeri olmalıdır. Eğer hata yaparsak en üstteki yön tuşlarını kullanıp düzeltme yapabiliriz. Son değeri de yazdıktan sonra Eşittir düğmesine basmamız yeterlidir.

Sonuç daha önce bulduğumuz gibi 0.3336 (%33.36) olacaktır.

Eğer P(0.29 < Z < 1.00) alanının olasılığını hesaplamak isteseydik ...

... Lower: 0.29, Upper: 1.00 değerlerini girip hesaplama yapmamız yeterli olurdu.

Sonuç ise daha önce bulduğumuz gibi %22.73 olacaktır.
Casio fx-991EX bilimsel hesap makinesi ile standart normal dağılım hesaplaması bu kadar kolaydır.
SPSS'te Normal Dağılım
SPSS'te normal dağılım grafiği nasıl oluşturulur öğrenmeden önce 1200 veri biriminden oluşan, ortalaması 175.71 ve standart sapması 13.70 olan yukarıdaki örneğimize benzer bir veriseti kullanacağız. Bu nedenle önce CSV formatındaki veri setimizi SPSS'e yüklemeliyiz.1
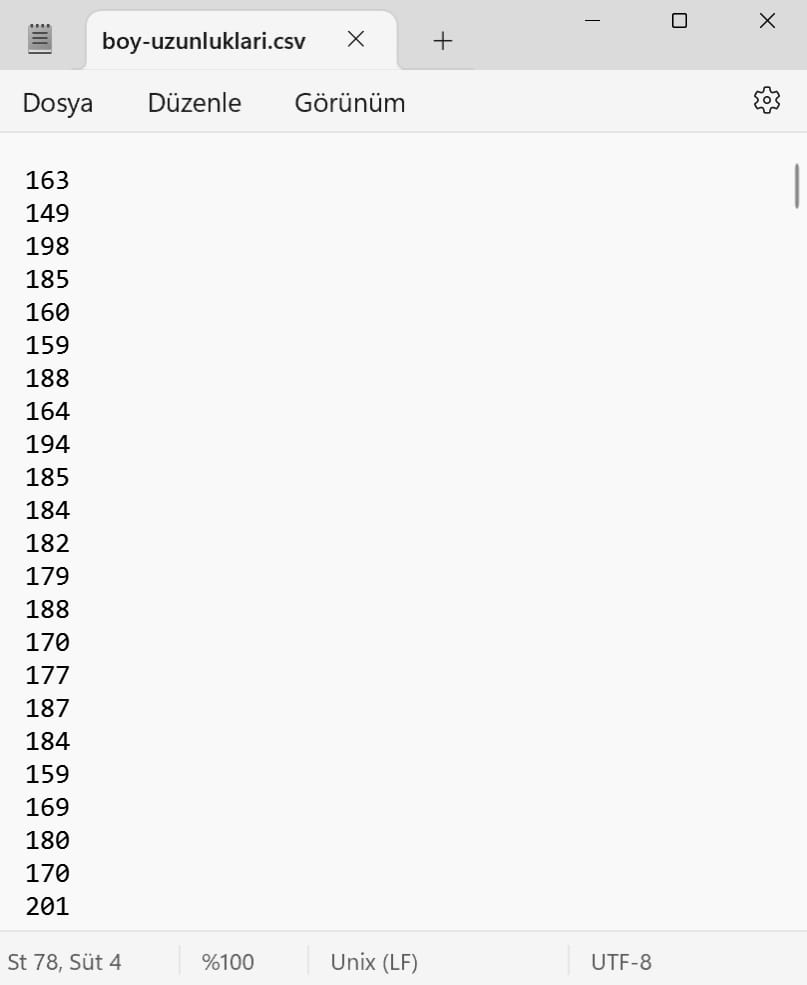
CSV dosyalarının açılımı comma-separated values (virgülle ayrılmış değerler) anlamına gelmektedir. Çok basit dosyalardır. Bilgisayarındaki metin defteri ile açabilirsiniz. Açtığınız zaman görseldeki gibi görünecektir.
csv dosyasını indirmek için yukarıdaki bağlantıya tıklayınız.
SPSS'i açtıktan sonra File > Open > Data yolunu izleyin.1
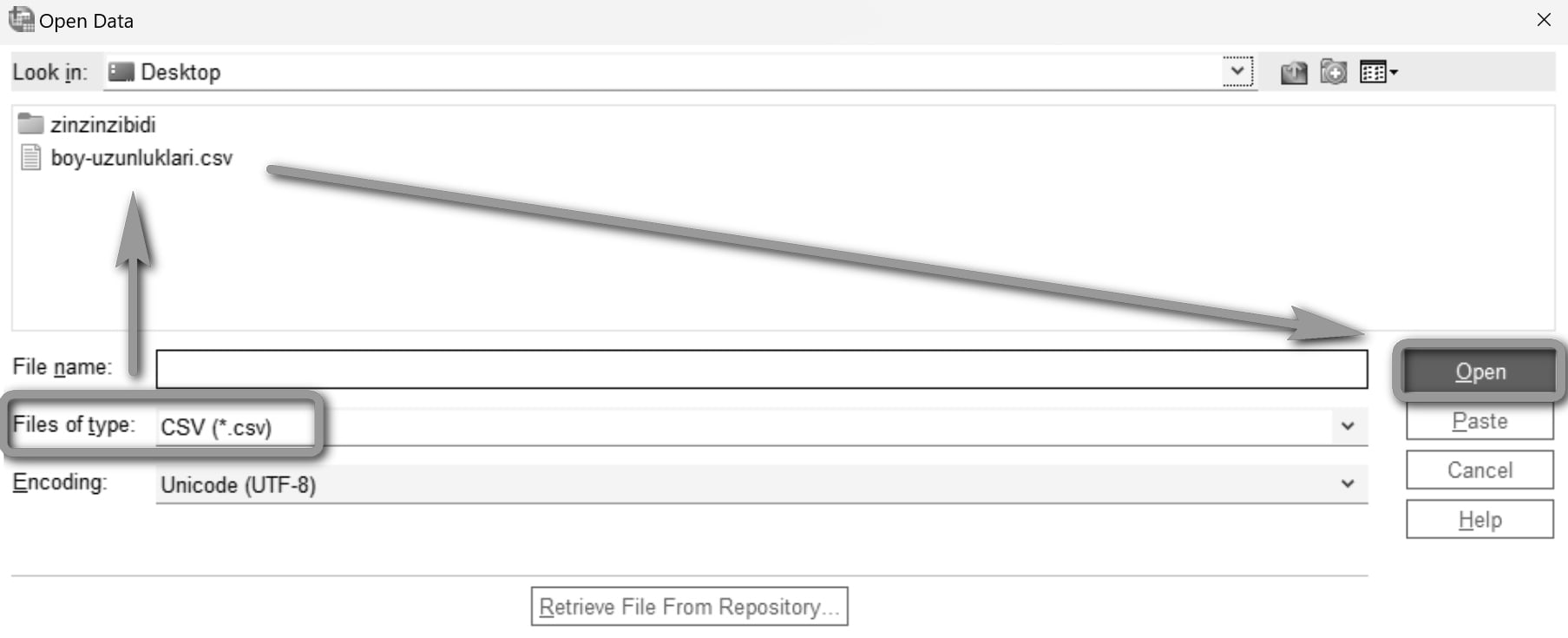
Önce Files of type'ı CSV seçin ve dosyayı da seçtikten sonra Open'a tıklayın. İndirdiğiniz dosyayı bulamazsanız bu pencerenin en üstünde Look in seçeneği var. Look in'deki listeden dosya yolunu bulun.
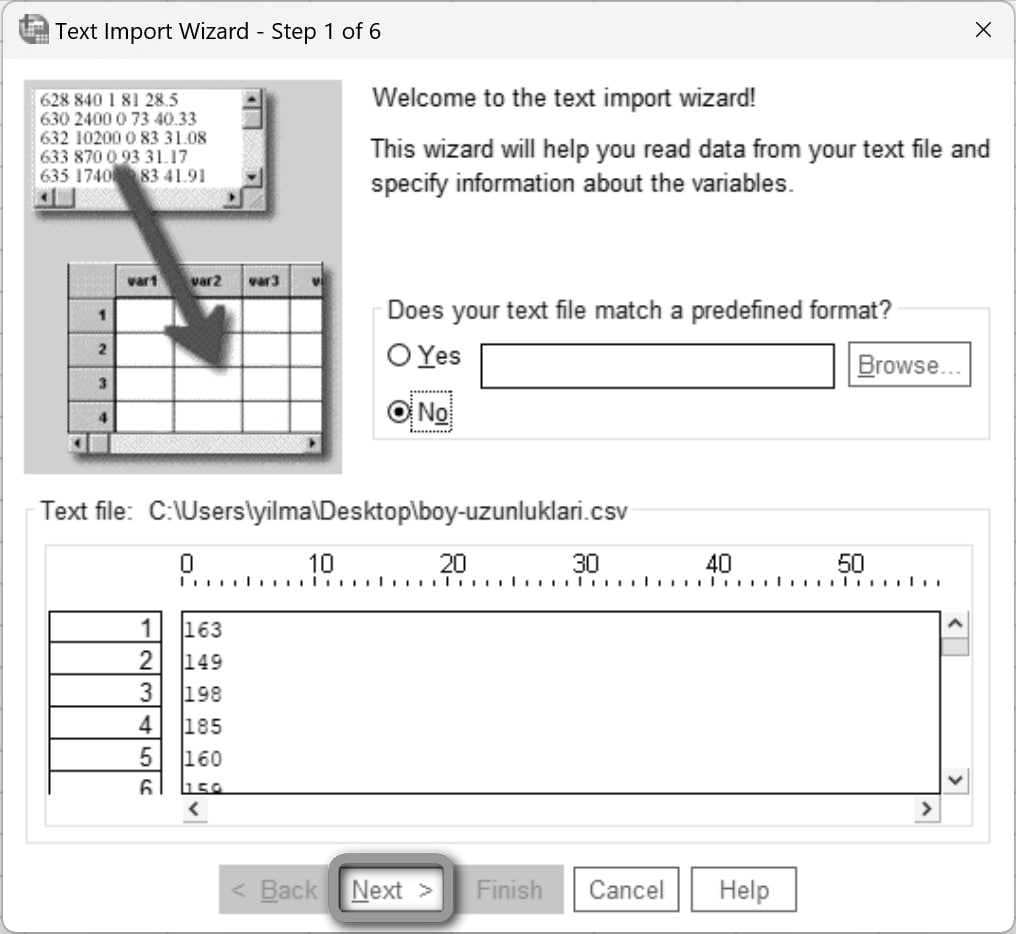
İlk adımda Next'e tıklayın.
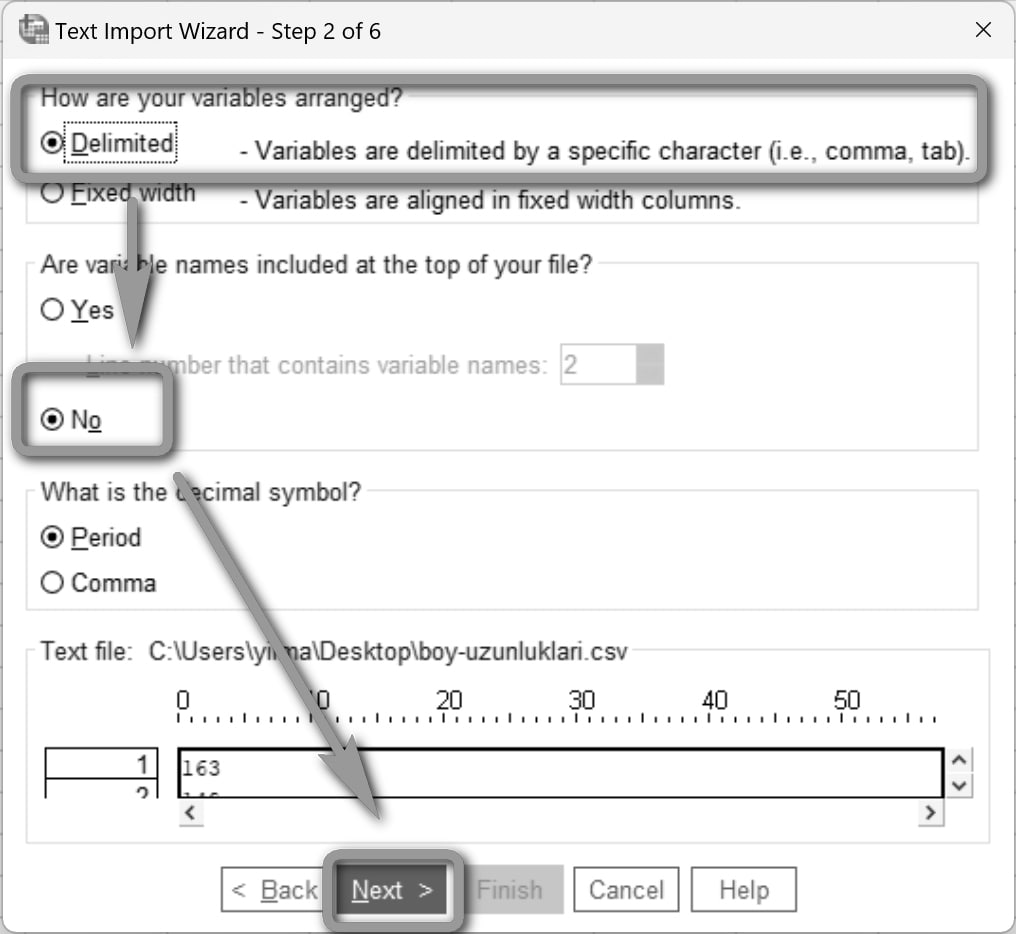
İkinci adımda görseldeki seçimleri yapın ve Next'e tıklayın.
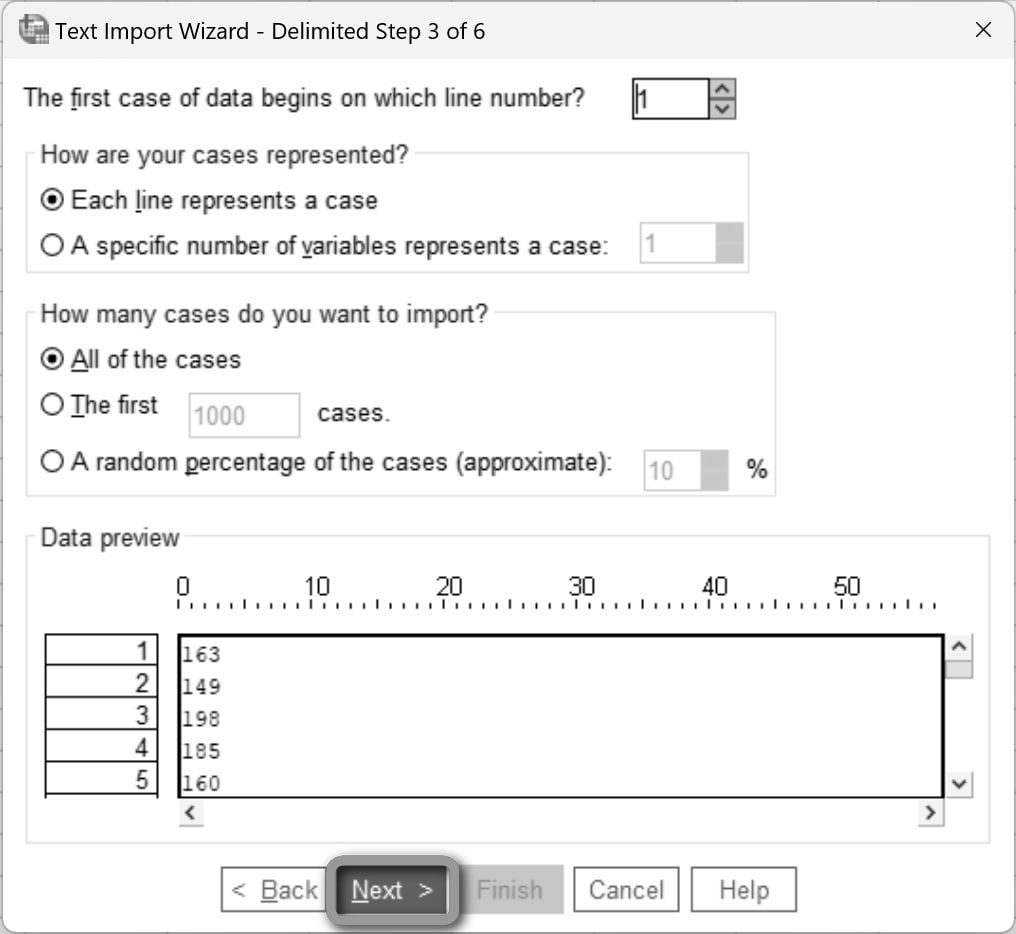
Üçüncü adımda Next'e tıklayın.
Dördüncü adımda da Next'e tıklayın.
Beşinci adımda değişkene bir ad verin. "boy" olabilir. Ardından Next'e tıklayın.
Son adımda Finish'e tıklayın.
Verilerimiz görseldeki gibi yüklenecek ve görüntülenecektir.
Şimdi geldik en kolay kısıma...
Menüden Graphs > Legacy Dialogs > Histogram... yolunu izleyin.
boy değişkenini Variable: alanına ekleyin.
Eklendikten sonra OK'a tıklayın.
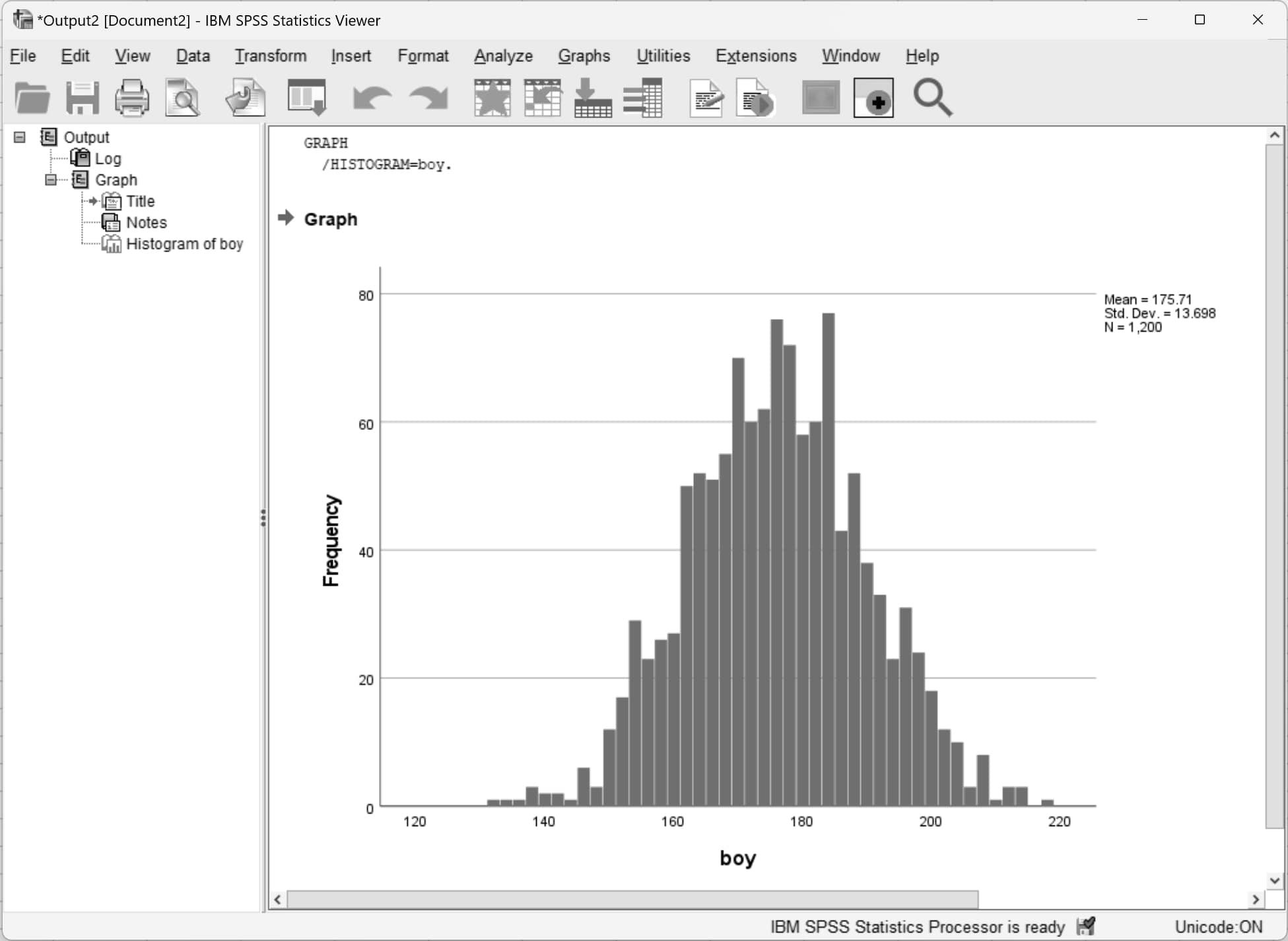
Output penceresi açılacak ve histogram görseldeki gibi oluşacaktır. Histogramın sağ üstünde veri setinin ortalaması, standart sapması ve veri sayısı yazmaktadır.
Grafiğin üzerine çift tıklayın. Chart Editor penceresi açılacaktır. Buradan sağ üstteki Histogram Simgesi'ni seçin ve Chart Editor penceresini kapatın.
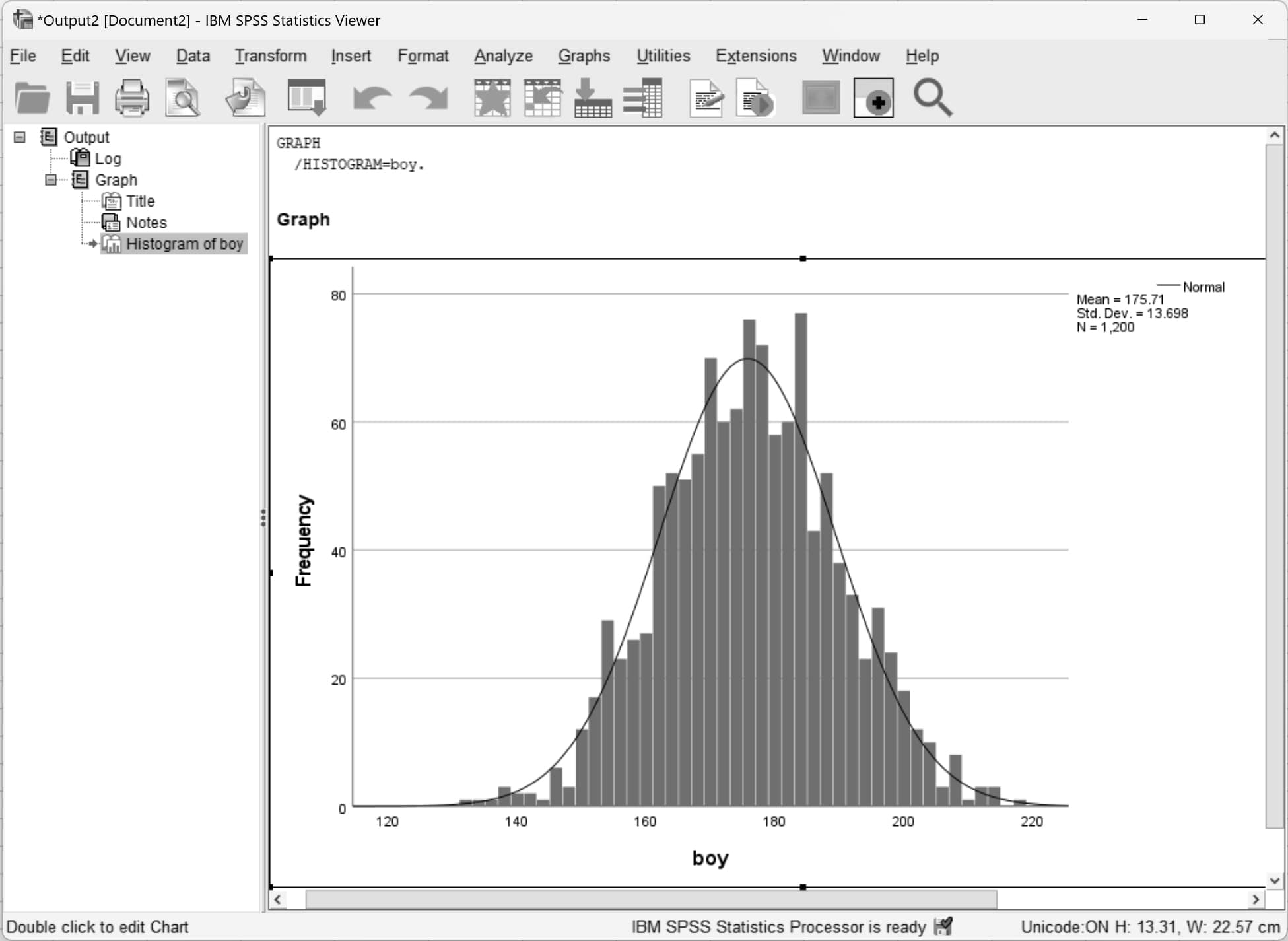
Artık histogram grafiğimizde histogram çizgisi de görüntülenecektir.
Dilerseniz grafiğin üzerine sağ tıklayıp resim olarak kaydedebilir ya da Word, PDF belgesi olarak dışarı aktarabilirsiniz. Grafiği paylaşmak isterseniz bunlar yeterli olacaktır.
Python ile Normal Dağılım
Python'da normal dağılım grafiğini Pandas, Matplotlib ve Seaborn kütüphaneleri ile oluşturabiliriz. Pandas verileri okumaya yarar. Matplotlib grafiği, Seaborn ise histogram çizgisini oluşturur.
İlk olarak boy-uzunluklari.csv dosyasını indirmeliyiz. İndirmek için yukarıdaki bağlantıya tıklayın.
Yukarıdaki kodlar normal dağılım grafiğini çizecektir. Fakat dikkat etmemiz gereken nokta csv dosyasını doğru okutmamız. .py ya da .ipynb dosyanız masaüstünde ise csv dosyası da masaüstünde olmalıdır. Tavsiyem PyCharm'da bir proje klasörü oluşturmanız ve csv dosyasını main.py dosyasının olduğu aynı klasörde bulundurmanız. PyCharm'da Python kütüphanesi eklemesi diğer editörlere göre çok daha kolaydır.
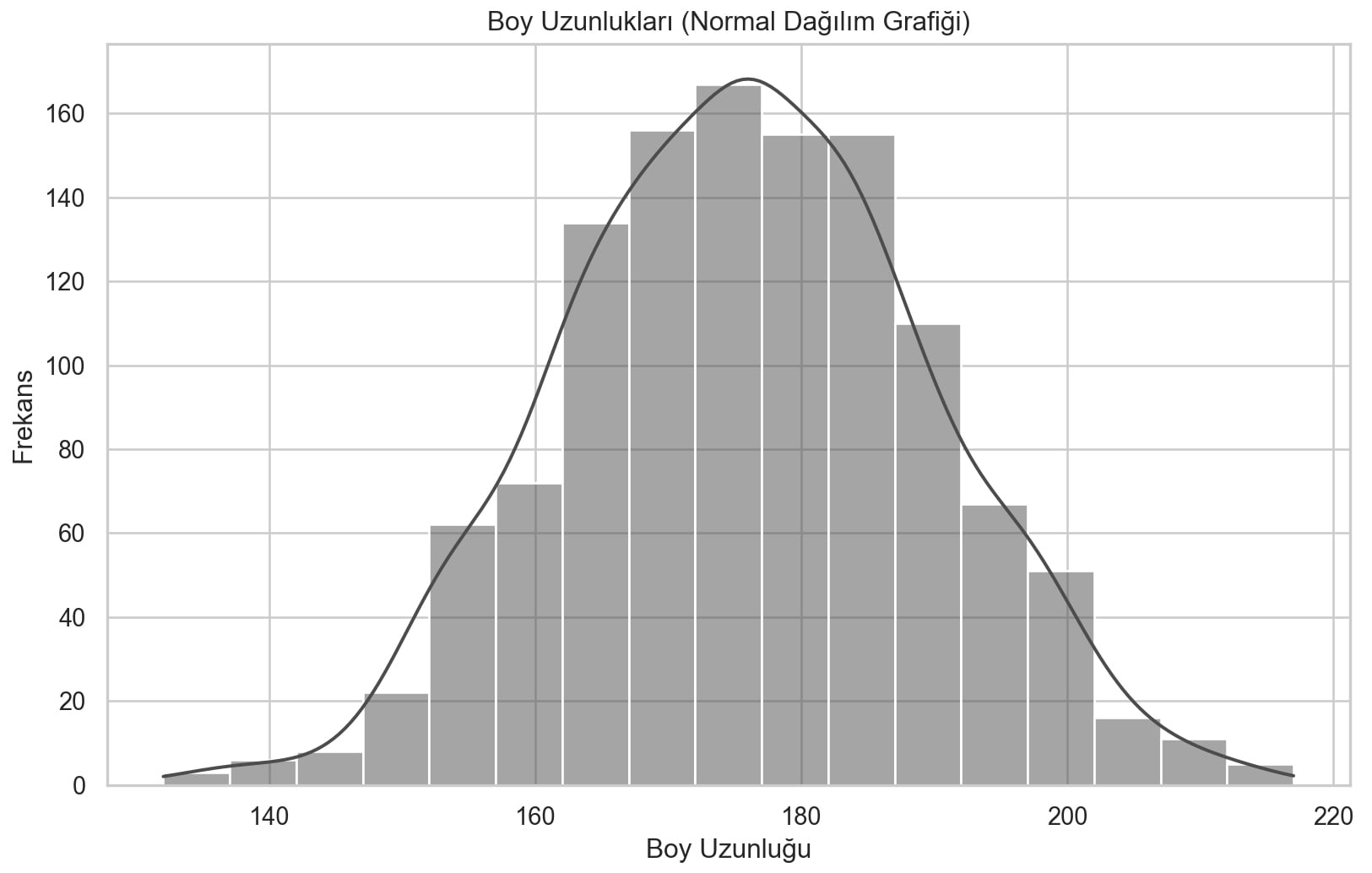
Kodları çalıştırdığımızda Matplotlib normal dağılım grafiğini görseldeki gibi oluşturacaktır.
Python ile Standart Normal Dağılım
Aynı veri setini standart normal dağılım grafiği olarak göstermek istersek Pandas ve Matplotlib kütüphaneleri ile birlikte NumPy ve SciPy kütüphanelerini de kullanmalıyız.
Python kodlarımızı çalıştırdığımızda ...
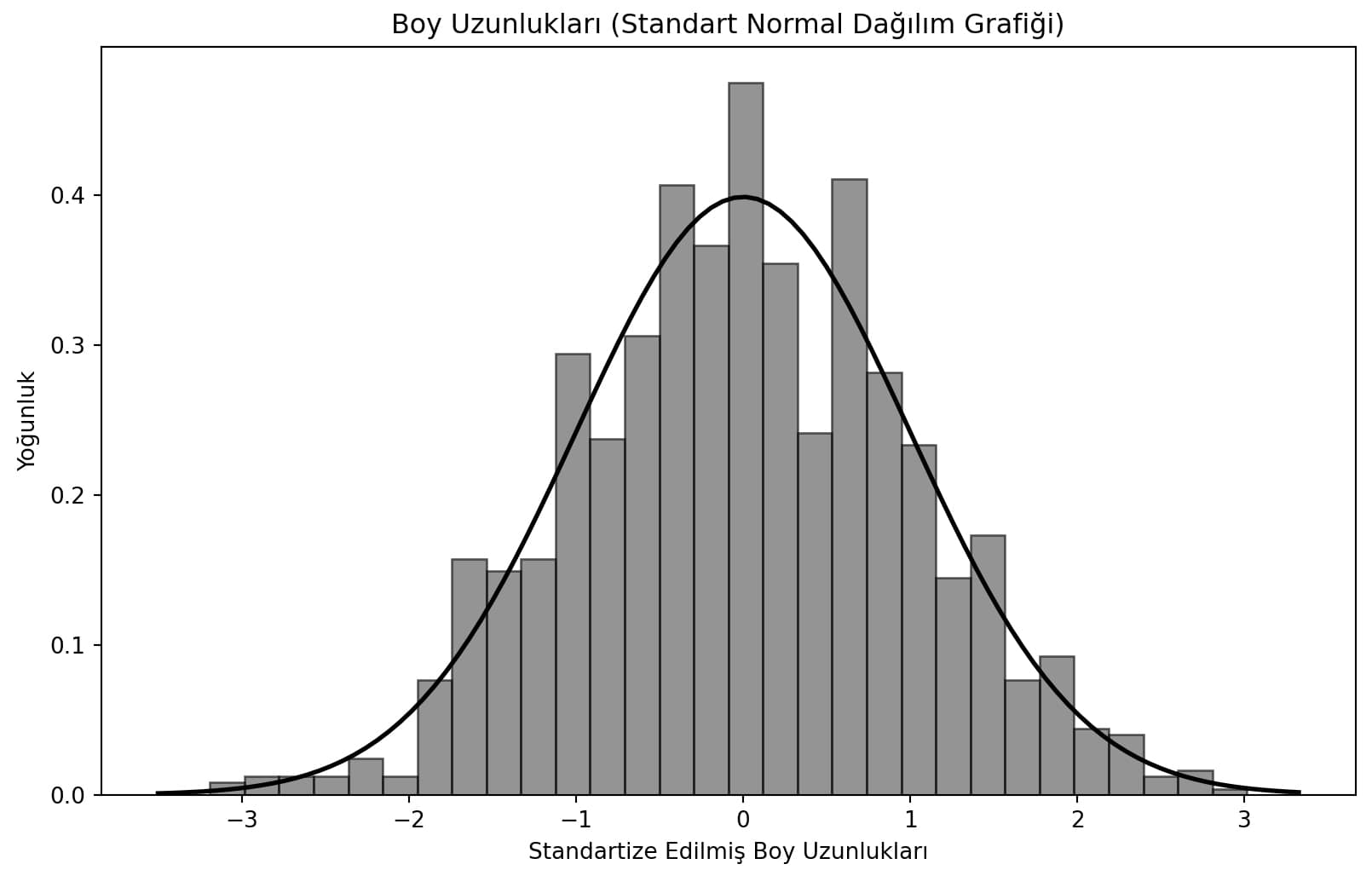
... boy uzunluklarının standart normal dağılım grafiğini elde edebileceğiz.
Python ile Normal Dağılım ve Standart Normal Dağılım grafiği oluşturması bu kadar. Umarım işinize yarar. Dersi bitirmeden önce tavsiyem aşağıdaki soruları çözmeniz ve normal dağılımı uygulamalı olarak tekrar etmeniz.
Sıra Sizde
Uygulama: Bir firmada çalışanların kiloları ölçülmüş ağırlıkların normal dağılım sergilediği gözlemlenmiştir. Ağırlıkların ortalaması 68 kg, standart sapması 16 kg'dır. Buna göre
- 90 kg'dan fazla çalışan olma olasılığı kaçtır?
- 70 - 80 kg arasında çalışan olma olasılığı kaçtır?
- 60 kg'dan az çalışan olma olasılığı kaçtır?
Yanıt 1 - İlk olarak 90 kg'dan fazla çalışan olma olasılığına bakacağız.
Normal dağılımı, standart normal dağılıma çevirdiğimizde Z değerini 1.38 buluruz.
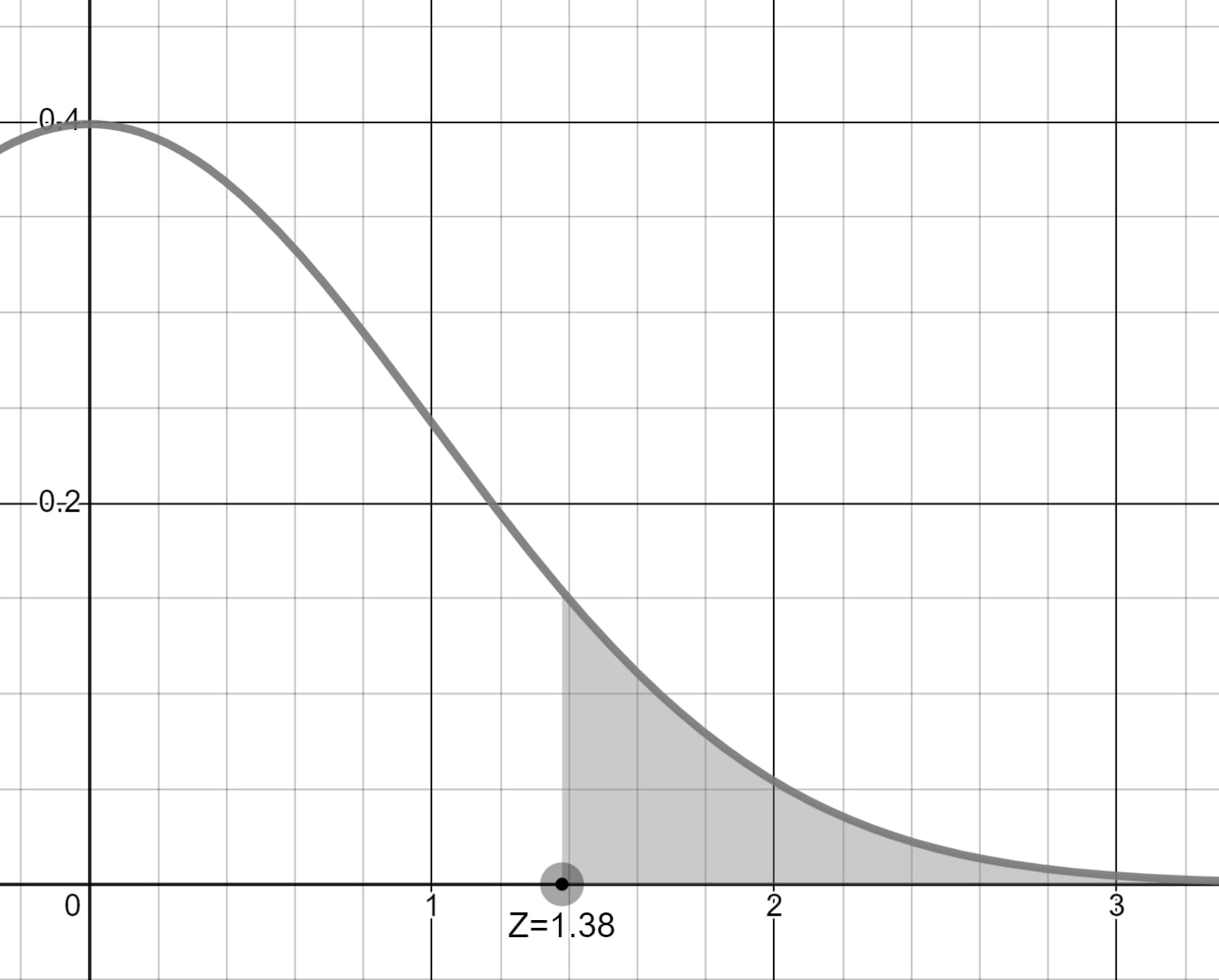
Soruda 90 kg'dan fazla sorulduğu için 1.38 Z değerinin yukarısındaki alanın olasılığını hesaplayacağız.
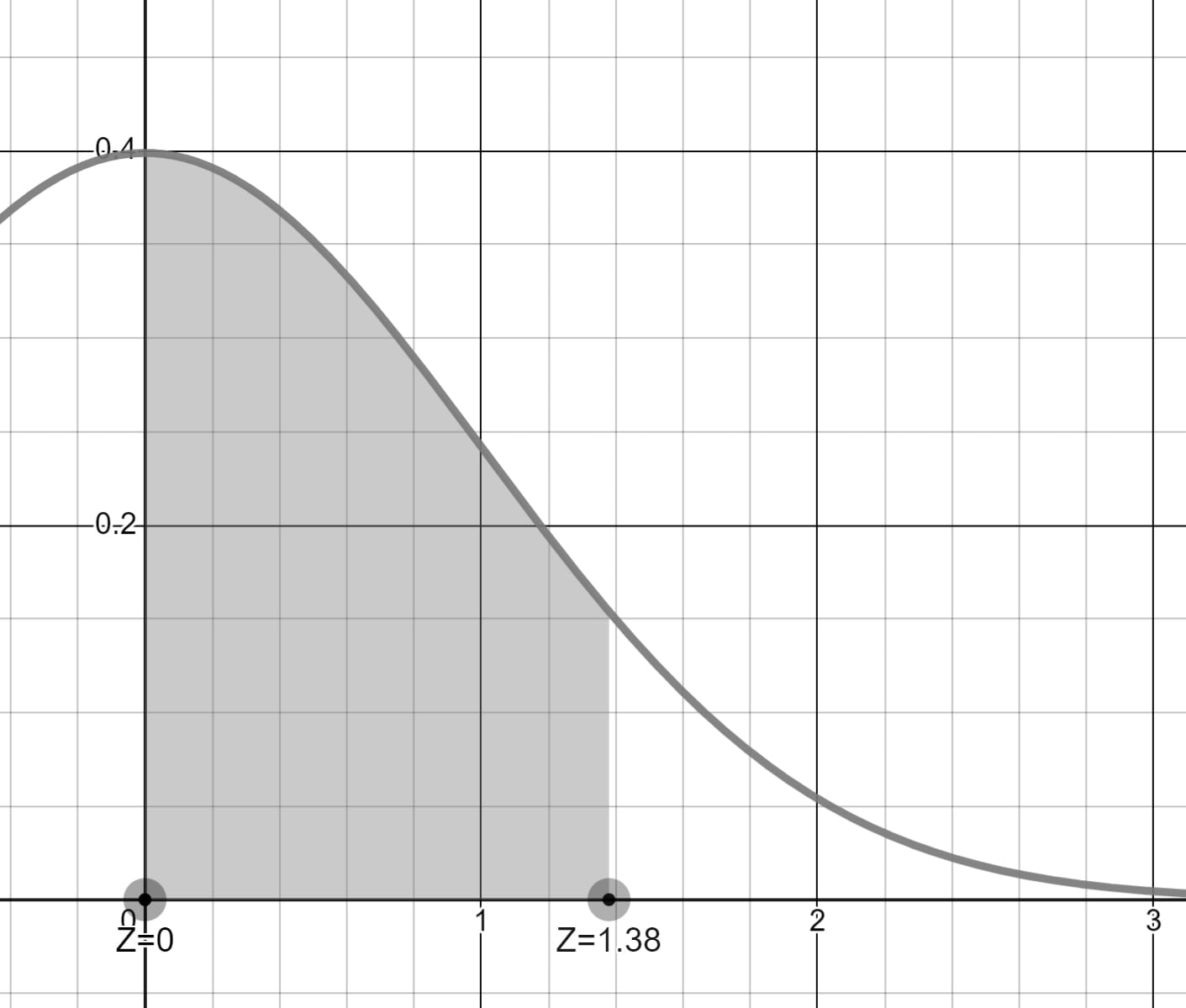
Histogram'ın sağ yarısının %50 olasılığa sahip olduğunu biliyoruz. O zaman %50'den P(0 < Z < 1.38) aralığındaki olasılığı çıkarırsak 90 kg'dan fazla çalışanların olasılığını bulabiliriz.
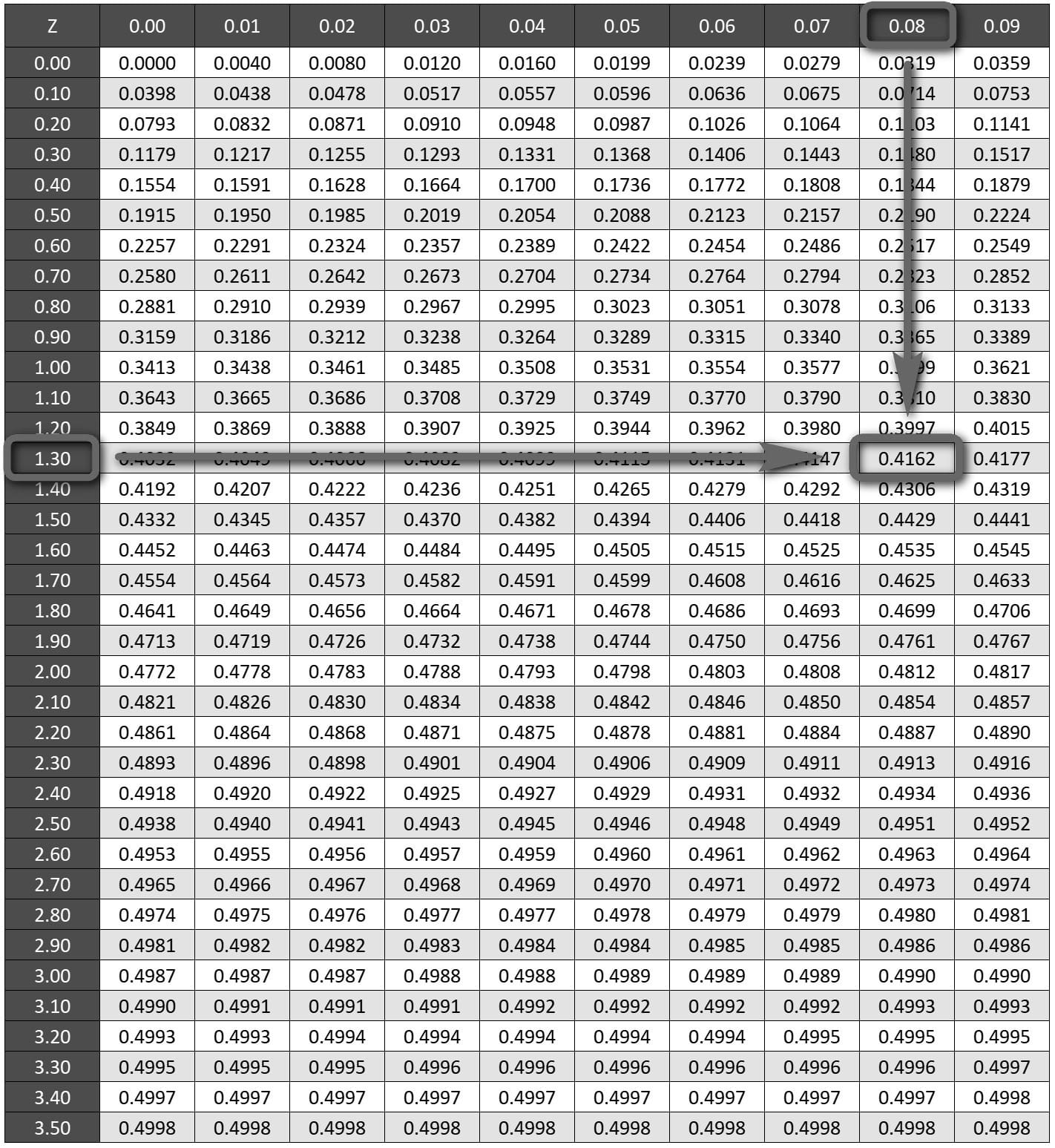
z-Tablosunda 1.30 ve 0.08 eksenlerinin kesiştiği hücredeki olasılık değeri 0.4162 (%41.62)'dir.

%50'den %41.62'yi çıkarırsak 90 kg'dan fazla çalışan olma olasılığını %8.38 buluruz.
Yanıt 2 - 70 - 80 kg arasında çalışan olma olasılığına bakalım.
70 ve 80 kg değerlerini standartize ettiğimizde 0.13 ve 0.75 Z değerlerini elde ederiz.
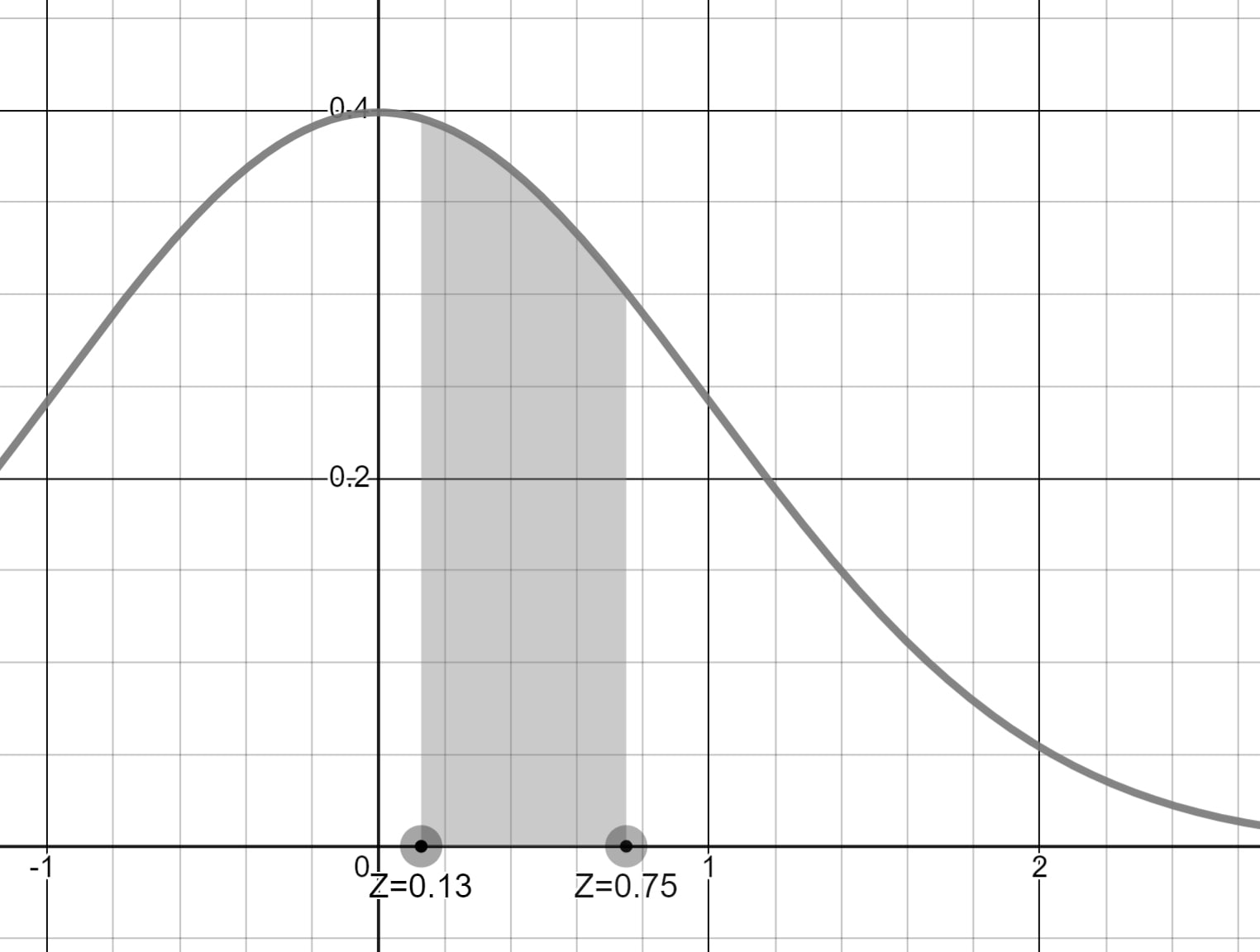
Soruda bu aralığın olasılığı sorulmaktadır.
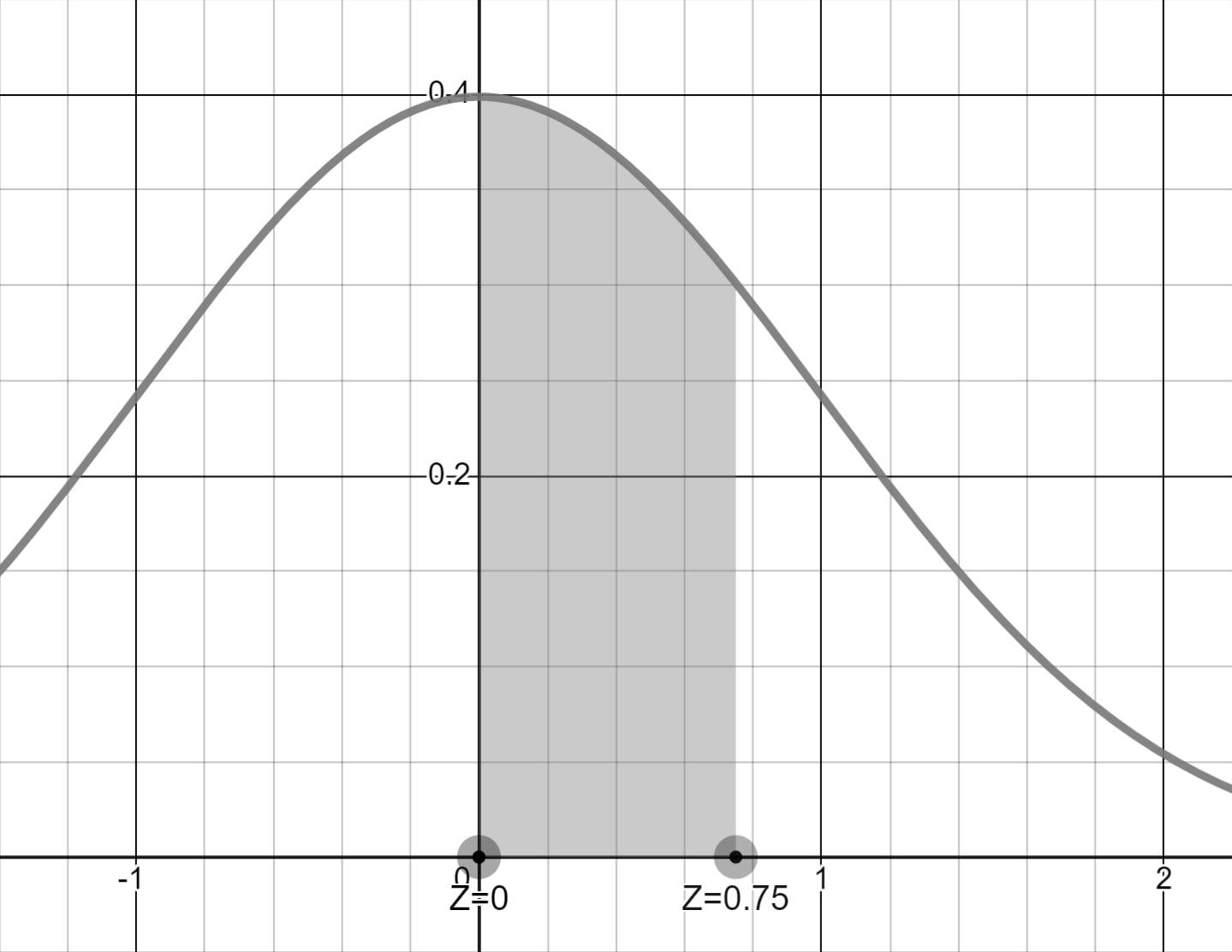
P(0 < Z < 0.75) aralığından ...
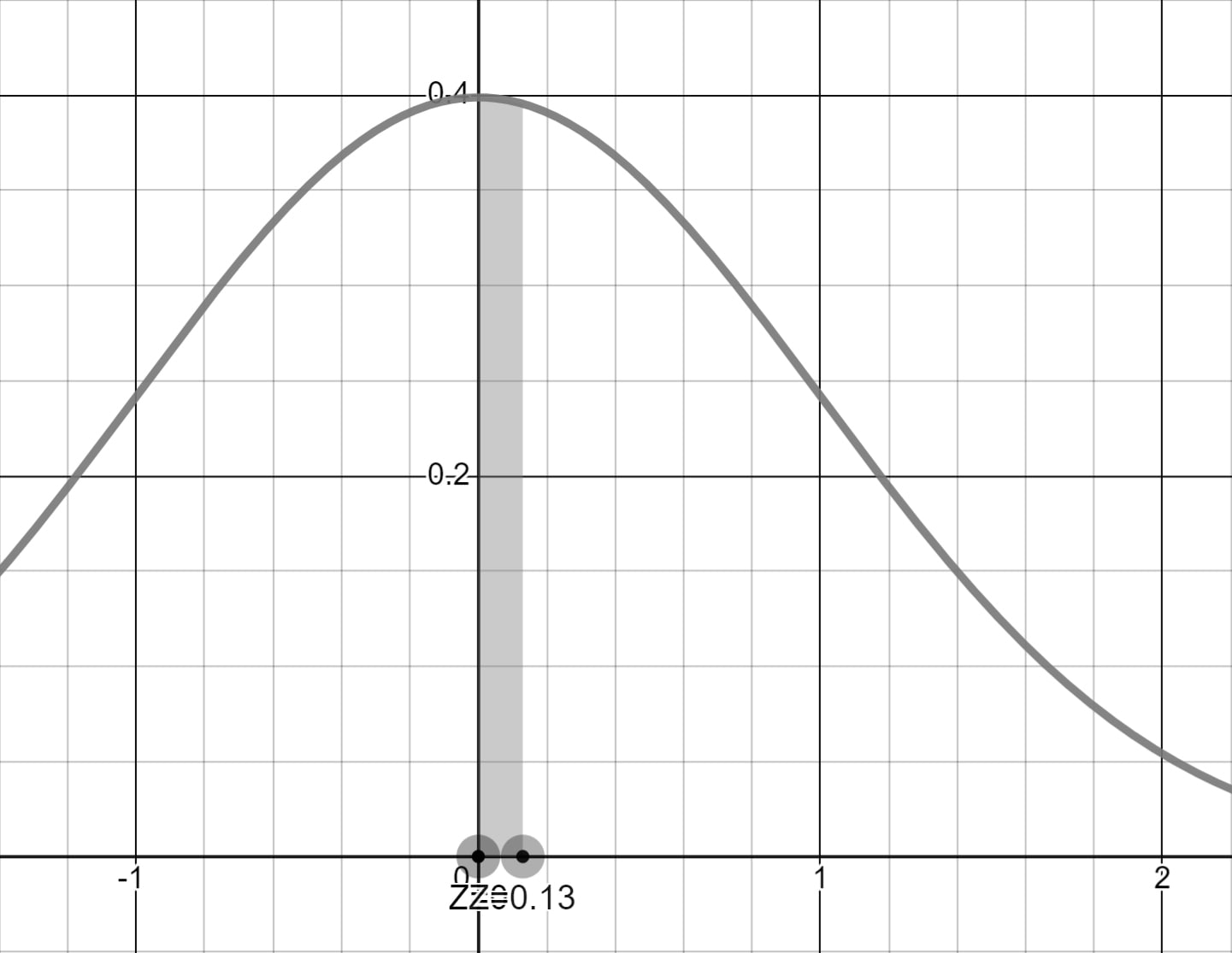
... P(0 < Z < 0.13) aralığını çıkarırsak aradığımız sonucu elde ederiz.

z-Tablosunda 0.75 Z değerine karşılık gelen 0.2734'den 0.13 Z değerine karşılık gelen 0.0517 olasılığını çıkardığımızda 0.2217 olasılığını elde ederiz.
Bu nedenle 70 - 80 kg arasında çalışan olma olasılığı %22.17'dir sonucuna varırız.
Yanıt 3 - Son olarak 60 kg'dan az çalışan olma olasılığı sorulmakta.
60 kg'ı standartize ettiğimizde Z değerini 0.50 buluruz.
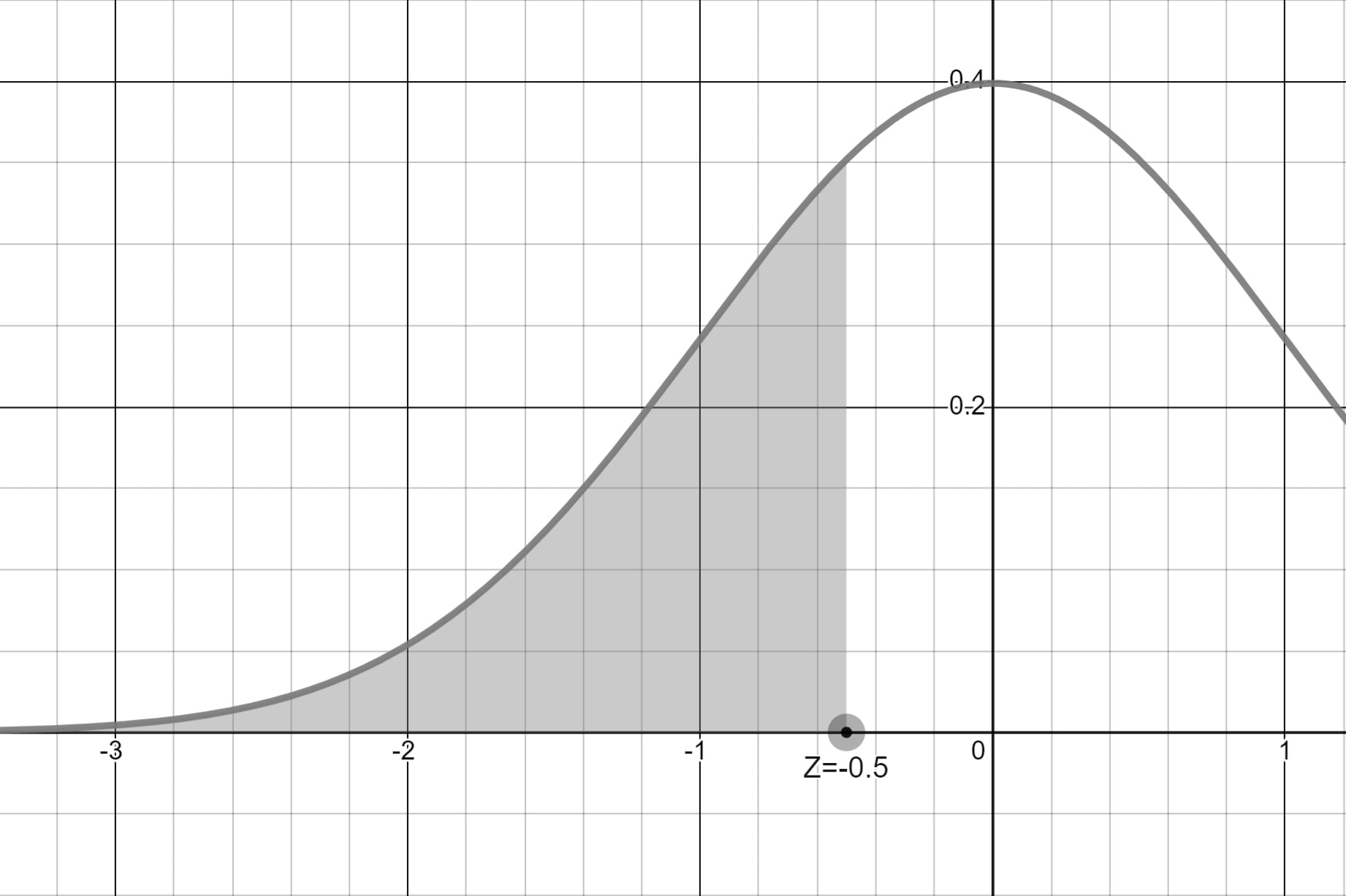
Soruda 60 kg'dan az sorulduğu için -0.50 Z değerinden küçük alanın olasılığını bulmalıyız.
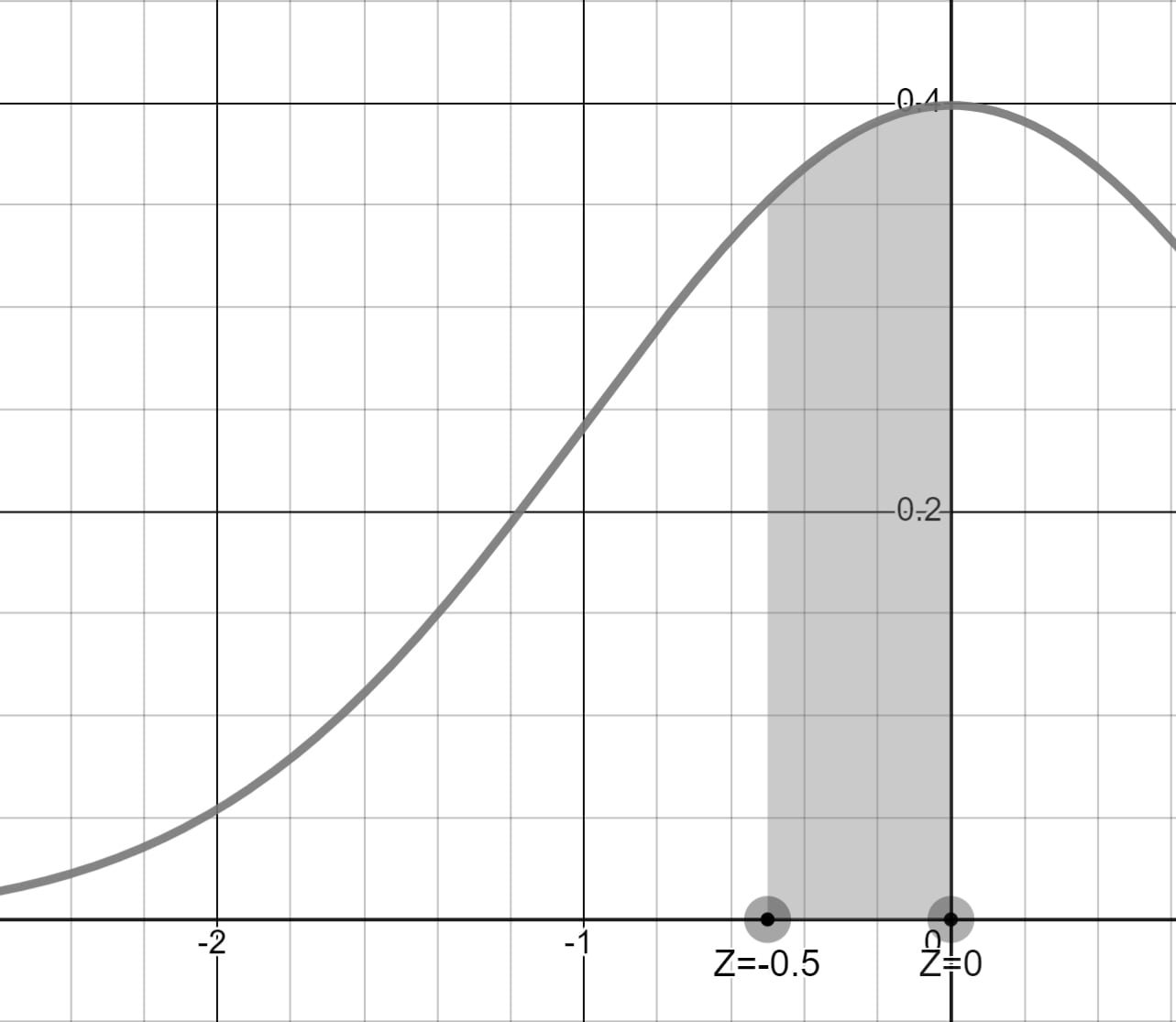
Simetri özelliğinden yararlanıp grafiğin sol yarısına ait %50 olasılıktan P(-0.50 < Z < 0) aralığındaki olasılığı çıkarmamız yeterlidir.

z-Tablosunda 0.50 ve 0.00 eksenlerinin kesiştiği hücrenin değeri 0.1915'tir. %50'den %19.15'i çıkardığımızda 60 kg'dan az çalışan olma olasılığını %30.85 bulabiliriz.
Evet hepsi bu kadar. Soruları çözmeye başlamadan önce soruda verilen değerlere göre standart normal dağılım grafiğini boş bir kâğıda çizmeniz ve çözümü daha sonra hesaplamanız soruları çok daha kolay çözmenizi sağlayacaktır.