İstatistik derslerini tablet üzerinden çalışmanız şiddetle tavsiye olunur.

Olasılık Teorisi

İstatistiğin temelini olasılık teoremi oluşturur. Bu bölümde olasılık teorisine ve olasılıkta kullanılan temel kavramlara değinilecektir. Bir sonraki Normal Dağılım dersinin de temelini bu ders oluşturmaktadır.

Temel Matematik Kavramları

Temel Olasılık Terimleri

Bayes Teoremi

Rassal Değişken

Olasılık Fonksiyonu

Olasılık Yoğunluk Fonksiyonu

Derse başlamadan hemen belirteyim. P harfi matematikte olasılığı simgelemektedir. İngilizce Probability'nin (Olasılık'ın) kısaltmasıdır.

Temel Matematik Kavramları

Olasılık terimlerinden önce temel bazı matematik kavramlarına ve bunların nasıl kullanılıdına değinmeliyiz.

Faktöriyel

1'den n'ye kadar olan pozitif tamsayıların çarpımına n faktöriyel denir ve n! sembolü ile gösterilir. ! (ünlem) işareti matematikte daima faktöriyeli belirtmektedir.

\[ n! = n \cdot (n-1) \cdot (n-2) \cdot ... \cdot 3 \cdot 2 \cdot 1 \]

biçiminde yazılır ve 0! daima 1'e eşittir.

\[ 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 \] \[ {6! \over 3!} = {6 \cdot 5 \cdot 4 \cdot \cancel{3!} \over \cancel{3!}} = 6 \cdot 5 \cdot 4 = 120 \] \[ (8-5)! = 3! = 3 \cdot 2 \cdot 1 = 6 \]

Örnekleri verilebilir. Görüldüğü gibi kullanımı oldukça basittir.

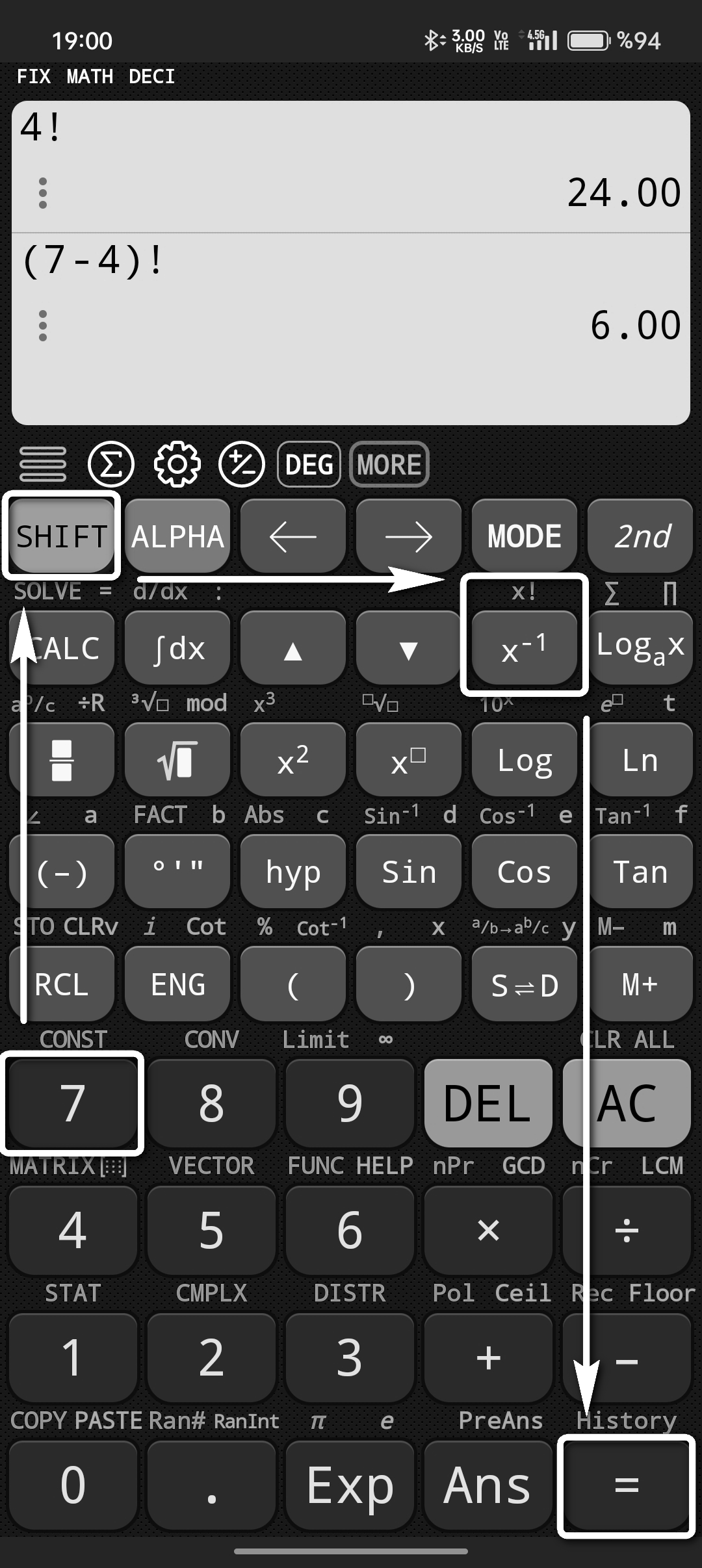
Bilimsel hesap makinelerinde faktöriyel hesaplaması çok kolaydır. Yukarıdaki örnekte hesap sonuçlarını görebiliriz. 7! faktöriyeli hesaplamak istersek öncelikle 7 sayısını yazdıktan sonra SHIFT'e tıklamalı, ardından x^-1 tuşuna basmalıyız. x^-1 tuşunun üzerinde sarı renk ile x! yazıldığını görebilirsiniz. Bu SHIFT'e basılması durumunda hangi tuşun etkinleşeceğini belirtmektedir. Bu nedenle daima SHIFT tuşunu kullanıyoruz.

Kullandığım hesap makinesinin Google Play adresine buradan ulaşabilirsiniz.

Fiziki hesap makinesi Casio fx-991EX'te de aynı şekilde 7! faktöriyeli hesaplayabiliriz.

Excel’de faktöriyel hesaplamak için
=ÇARPINIM() formülünü kullanabiliriz.

Permütasyon

Sıralama denildiğinde aklımıza daima permütasyon gelmelidir. n sayılı bir kümeden r tane eleman çektiğimizde bunları kaç farklı şekilde sıralayabileceğimizi permütasyon gösterir.

\[ P(n,r) = { n! \over (n-r)!} \]

formülüdür. P(n,r) notasyonu ile gösterildiği gibi nPr ile de gösterilmektedir. İki ifade de aynıdır.

Örneğin; A, B ve C kişilerinden oluşan 3 kişilik bir gruptan 2 farklı kişi seçmek isteyelim. Seçtiğimiz bu kişiler kendi aralarında kaç farklı şekilde sıralanabilir?

\[ P(3,2) = { 3! \over (3-2)!} \] \[ P(3,2) = { 3! \over 1!} = { 3 \cdot 2 \cdot 1! \over 1!} = 6 \]

Sonuç altıdır. Bu sıralamayı tek tek yazmak istersek:
AB, BA, AC, CA, BC, CB olduğunu görebiliriz.

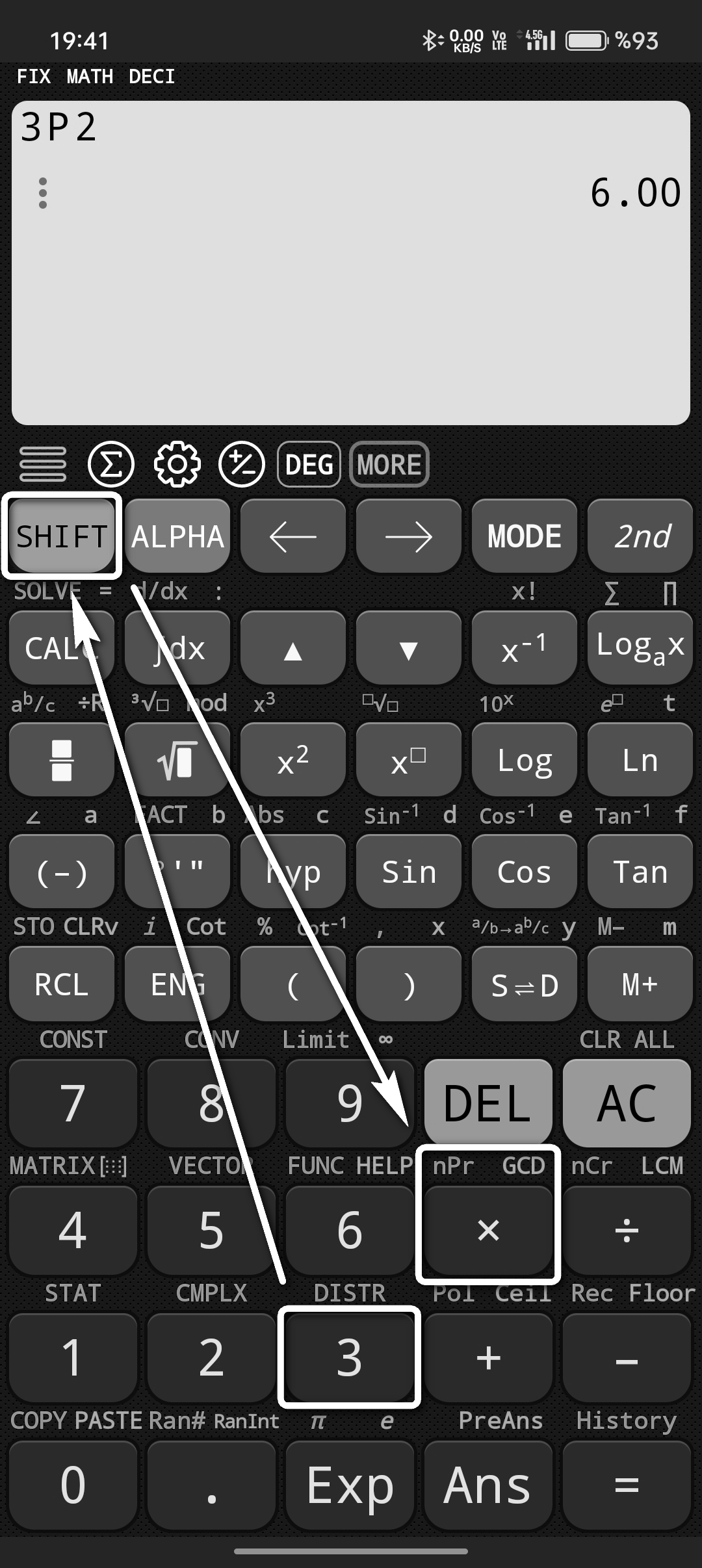
Bu işlemi bilimsel hesap makinemizde yapmak istediğimizde öncelikle n değeri olan 3'ü yazıyoruz. Ardından SHIFT'e tıklıyoruz. Son olarak x (çarpım) tuşuna basıyoruz. r değeri olan 2'yi de yazıp = (eşittir) dediğimizde sonucun 6 olduğunu görebiliriz.

Çarpım tuşunun üzerinde sarı renk ile nPr yazdığını fark etmiş olabilirsiniz. Bilimsel hesap makinelerinin tümünde bu ifade permütasyonu belirtmektedir.

Aynı işlemi Casio fx-991EX'te de yapabilirsiniz.

Excel’de permütasyon hesaplamak için
=PERMÜTASYON(n değeri; r değeri) formülünü kullanabiliriz.

Kombinasyon

Seçim denildiğinde ise aklımıza daima kombinasyon gelmelidir. n sayılı bir kümeden r tane elemanı kaç farklı şekilde seçebileceğimizi kombinasyon verir.

\[ C(n,r) = { n! \over (n-r)! r!} \]

formülüdür. Permütasyona benzer. Farkı paydada fazladan r! faktöriyel olmasıdır. C(n,r) notasyonu ile gösterildiği gibi nCr ile de gösterilmektedir. İki ifade aynı anlama gelmektedir.

Örneğin; A, B ve C kişilerinden oluşan 3 kişilik bir gruptan 2 kişiyi kaç farklı şekilde seçebiliriz?

\[ C(3,2) = { 3! \over (3-2)! 2!} \] \[ C(3,2) = { 3! \over 1! 2! } = { 3 \cdot 2! \over 2!} = 3 \]

Yanıt 3'tür. Bu seçimi tek tek yazmak istersek: AB, AC, BC olduğunu görebiliriz. Burada sıralama önemli değildir. Seçim önemlidir. Örneğin; AB seçimi ile BA seçimi aynıdır.

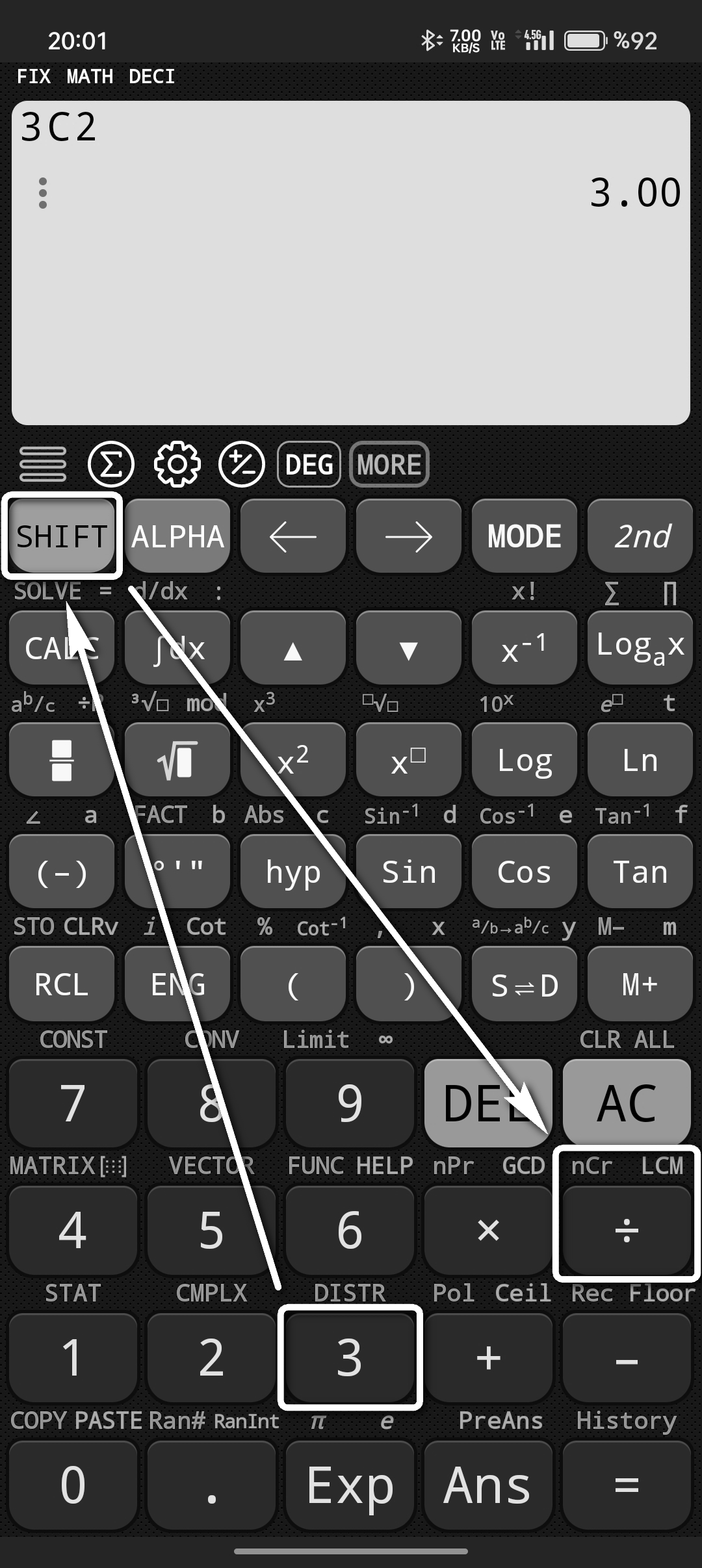
Bu işlemi bilimsel hesap makinemizde yapmak istediğimizde öncelikle n değeri olan 3'ü yazıyoruz. Ardından SHIFT'e tıklıyoruz. Son olarak ÷ (bölüm) tuşuna basıyoruz. r değeri olan 2'yi de yazıp = (eşittir) dediğimizde sonucun 3 olduğunu görebiliriz.

Bölüm tuşunun üzerinde sarı renk ile nCr yazılmıştır. Bilimsel hesap makinelerinin tümünde bu ifade kombinasyonu belirtmektedir.

Excel’de kombinasyon hesaplamak için
=KOMBİNASYON(n değeri; r değeri) formülünü kullanabiliriz.

Temel Olasılık Terimleri

Bu alt bölümde bilmemiz gereken temel olasılık terimleri açıklanacaktır.

Rastgele Deney

Birden çok gözlemden sadece bir tanesinin gerçekleşmesine deney denir. Aynı şartlar altında farklı sonuçlar veren deneyler ise rastgele deney olarak adlandırılır.

Madeni para bir kez atılması sonucu tura gelmesi rastgele deneye örnek verilebilir. Bir zar atışında 5 sayısının gelmesi de rastgele deneydir.

Örneklem Uzayı

Deney ile ilgili tüm olası sonuçların toplandığı kümedir. S harfi ile gösterilir.

Bir madeni para havaya atıldığında yazı ya da tura gelebilir. Örneklem uzayı S = {Y, T} olur. 2 elemanlıdır.

İki madeni para havaya atıldığında örneklem uzayı S = {YY, YT, TY, TT} olur. 4 elemanlıdır.

"Bir araçta 6 kişi vardır. Rastgele 4 kişi seçtiğimizde bunun örneklem uzayı nedir?" sorusunu biraz önce öğrendiğimiz kombinasyon ile rahatlıkla yanıtlayabiliriz.

C(6,4) = 15'tir. Bu nedenle bu deneyin örneklem uzayı S = 15'tir deriz.

Olay

Bir örneklem uzayında bir ya da birden fazla sonuç söz konusu ise buna olay denir.

Örneğin; iki madeni paranın havaya atılması sonucu oluşan örneklem uzayını S = {YY, YT, TY, TT} bulmuştuk. Yazı-Yazı ve Tura-Tura gelmesinin olasılığı kaç diye soralım?

Bu olayı A harfi ile ifade edelim. (Olaya dilediğimiz harfi verebiliriz) A = {YY, TT}'dir.

Yazı-Yazı ve Tura-Tura Gelme Olasılığı
= [A = {YY, TT}] / [S = {YY, YT, TY, TT}] = A / S = 2 / 4 = 1 / 2
= 0.50 = %50'dir diyebiliriz.

Bayes Teoremi

Birden çok etkenin aynı sonucu verdiği durumlarda bazen sonuç bilindiği halde bunun hangi sebepten kaynaklandığı bilinmeyebilir. Bu gibi durumlarda Bayes Teoreminden faydalanılır. Gelin bunu formülle anlatmak yerine soru üzerinde anlatalım.

A Sınıfı

B Sınıfı

Toplam

İngilizce Bilen

İngilizce Bilmeyen

Toplam

İngilizce bilen birinin A sınıfından olma olasılığı kaçtır?

Her iki sınıf da 40 kişiden oluşmaktadır.

A sınıfında İngilizce bilenlerin olasılığı 5/40 = 1/8'dir.

Seçilen kişinin A sınıfından olma olasılığı 40/80 = 1/2'dir.

Bu nedenle hem A sınıfından olma hem de İngilizce bilme olasılığı (1/8)x(1/2) = 1/16'dır.

Şimdi tüm olası sonuçlara bakalım...

İngilizce bilen birinin B sınıfından olma olasılığı (10/40)x(40/80) = 1/8'dir.

Herhangi bir sınıftan olup İngilizce bilme olasığı (1/16) + (1/8)'dir. Fakat soruda bizden İngilizce bilen birinin A sınıfından olma olasılığı sorulmuştur.

Sonuç olarak,

\[ P = { { 1 \over 16 } \over { { 1 \over 16 } + { 1 \over 8 } } } = { 1 \over 3 } \approx 0.3333 \]

İngilizce bildiğini bildiğimiz bir kişinin A sınıfından olma olasılığı %33.33'tür diyebiliriz.

Kafa karıştırıcı oldu farkındayım. Farklı bir örnek yapıp Bayes Teoremini pekiştirelim.

A Takımı

B Takımı

Toplam

İyi Oynuyor

Kötü Oynuyor

Toplam

Kötü oynayan birinin A takımından olma olasılığı kaçtır?

A takımında kötü oynayanların olasılığı 7/29'tur.

Seçilen oyuncunun A takımından olma olasılığı 29/81'dir.

Bu nedenle hem A takımından olma hem de kötü oynama olasılığı (7/29)x(29/81) = 7/81'dir.

Tüm olası sonuçlara bakalım...

Bu kişinin B takımından olup kötü oynama olasılığı (19/52)x(52/81) = 19/81'dir.

Herhangi bir takımdan olup kötü oynama olasığı 7/81 + 19/81'dir. Soruda bizden kötü oynayan birinin A takımından olma olasılığı sorulmuştu.

Sonuç olarak,

\[ P = { { 7 \over 81 } \over { { 7 \over 81 } + { 19 \over 81 } } } = { 7 \over 26 } \approx 0.2692 \]

Kötü oynadığını bildiğimiz bir oyuncunun A takımından olma olasılığı %26.92'dir diyebiliriz.

A takımda kötü oynayanların olasılığını hem A hem de B takımında kötü oynayanların olasılığına oranlıyoruz. Kolay değil mi?

Eğer hâlâ anlamadıysanız hiç üzülmeyin. Çünkü veri bilimi ve veri analizi kariyerimiz boyunca bu tür sorularla uğraşmayacağız. Vaktimizin büyük çoğunluğu veriler ile geçecek. Aynı zamanda yapay zekânın bugün çok ileri seviyelerde olması nedeniyle bu tür soruları ChatGPT gibi uygulamalara da sorabiliriz.

Rassal Değişken

Örneklem uzayındaki olayların benzersiz durumlarına rassal değişken denir. Kimi kaynaklarda rastgele değişken olarak da adlandırılır. İngilizce random variable'dır.

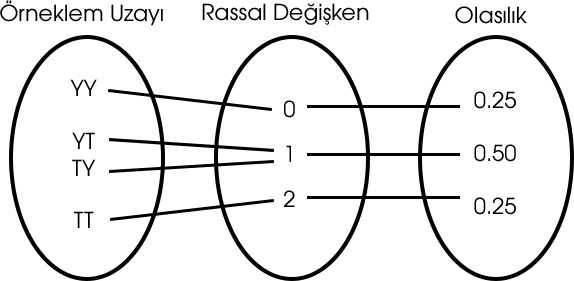
İki madeni paranın atılması sonucu örneklem uzayını
S = {YY, YT, TY, TT} bulmuştuk. Buradaki YT ve TY gelme olasılığı aslında aynıdır. Bu nedenle örneklem uzayında bu iki olay ayrı ayrı gösterilirken rassal değişken durumunda aynı kabul edilir.

Yukarıdaki görselde de görülebileceği üzere rassal değişkenleri bulurken örneklem uzayındaki her bir olayı öncelikle benzersiz olmalarına göre ayırıyoruz. Ardından 0, 1, 2 ... şekilde giden değişken tanımlamaları yapıyoruz. Üçüncü kümede ise olasılığı hesaplayabiliyoruz.

Örneğin; iki madeni paranın birlikte atılması sonucu yazı ve tura gelme olasılığı 1/2'dir. İlk parada yazı gelip ikinci parada tura gelebilir. Ya da ilk parada tura gelip ikinci parada yazı gelebilir. Bu iki olayı tek kabul ettiğimiz için rassal değişken olarak adlandırıyoruz.

Rassal değişkenler

Kesikli Rassal Değişken
Sürekli Rassal Değişken

olmak üzere iki türlüdür.

Kesikli Rassal Değişken

Zar atışı, para atışı gibi sonuçları tamsayı olan değişkenlerden oluşur. Temel Kavramlar dersinden hatırlayacağınız Aralıklı Veri (Discrete Data) gibi düşünebilirsiniz. Bir zar atışının sonucu 3.5 olamaz. Ya 3'tür ya da 4. Bu nedenle değerleri ondalıklı olmayan tüm rassal değişkenler, kesikli rassal değişken olarak adlandırılır.

Sürekli Rassal Değişken

Değerleri ondalıklı olabilen rassal değişkenlerdir. Temel Kavramlar dersindeki Sürekli Veri (Continuous Data) kavramına benzer. Örneğin hava sıcaklığı... Hava sıcaklığı 24°C olabileceği gibi 24.2°C de olabilir. Bu nedenle bu tür rasssal değişkenler, sürekli rassal değişken olarak adlandırılır. Sürekli rassal değişkenlere ait değerler bir doğru üzerindeki herhangi nokta olabilmektedir.

Kesikli ve sürekli rassal değişkenlerin fonksiyon durumu da vardır.

Olasılık Fonksiyonu

Kesikli olasılık fonksiyonu olarak da adlandırılır; fakat olasılık fonksiyonu denilince aklımıza daima kesikli rassal değişkenler gelmelidir.

f(x) = P(X) durumlarının tamamı olasılık fonksiyonudur.

\[ f(x) \geq 0 \] \[ \Sigma f(x) = 1 \]

iki koşuludur.

Örneğin; iki madeni paranın birlikte atılma durumunu ele alalım.

Toplam (Σ)

P(X)

0.25

0.50

0.25

TT 0, YT ve TY 1, YY ise 2 rassal değişkeni ile ifade edilsin. S = {YY, YT, TY, TT} örneklem uzayında TT gelme olasılığı 1/2 * 1/2'den 1/4, yani 0.25'tir. YY gelme olasığı da aynıdır. YT ya da TY gelme olasılığı ise 1/2, diğer bir ifade ile 0.50'dir. %50

İşte bu tabloya olasılık dağılım tablosu adı verilmektedir. P(2) = 0.25 diyebiliriz.

Olasılık Yoğunluk Fonksiyonu

Sürekli rassal değişkenlerden oluşan fonksiyondur. Bir sonraki derste öğreneceğimiz Normal Dağılım'ın temelini olasılık yoğunluk fonksiyonu oluşturur.

\[ f(x) \geq 0 \] \[ \int f(x)dx = 1 \]

iki koşuludur. Burada uzun S harfi şeklindeki simge matematikteki integrali belirtmektedir. Gözünüz korkmasın. Çok basit bir anlamı ve yine hesap makineleri yardımıyla çok basit bir hesaplaması vardır.

İntegral Nedir?

Bizim

\[ \int_a^b {f(x) dx} \]

şeklinde ifade ettiğimiz bu fonksiyonun

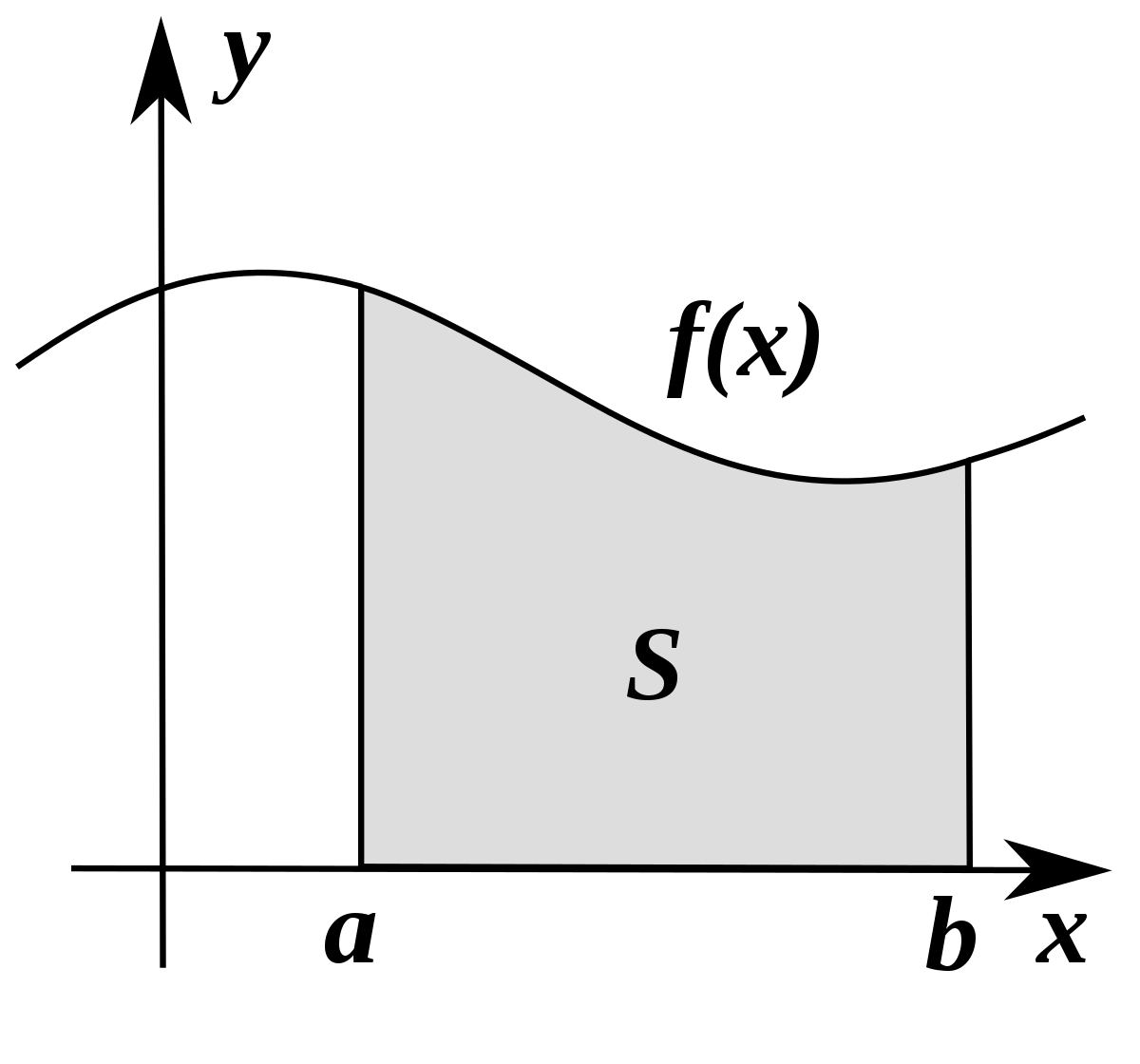
grafiği görseldeki gibidir. İntegral görselde fonksiyon çizgisi altında kalan ve S ile gösterilen alanı hesaplamak için kullanılır. Tek kullanımı budur. Verilen belirli bir aralık değeri ile fonksiyonun x ekseni ile arasında kalan alanı hesaplamak.

Örneğin; ekonometri bölümünü 4 yılda bitirmenin olasılık yoğunluk fonksiyonu aşağıdaki gibidir.

\[ \begin{equation} f(x) = \begin{cases} {3x^3 \over 244} = {0 \leq x \leq 4}\\ \\ \text{0 diger durumlarda} \end{cases} \end{equation} \]

Bir öğrencinin ekonometri bölümünü 3 yılda ya da 3 yıldan az sürede bitirme olasılığı nedir?

\[ P(0 \leq x \leq 3) = \int_0^3 {3x^3 \over 244} dx \]

İntegral alırken rassal değişkenin üssünü 1 artırırız. Paydayı da artırılan üs değeri kadar çarparız.

\[ P(0 \leq x \leq 3) = \int_0^3 {3x^3 \over 244} dx = \left.{3x^4 \over 244 \cdot 4} \right\vert_{0}^{3} \] \[ P(3) = {3\cdot3^4 \over 244 \cdot 4} \approx 0.2490 \] \[ P(0) = {3\cdot0^4 \over 244 \cdot 4} \approx 0.0000 \] \[ P(3) - P(0) = 0.2490 - 0.0000 \approx 0.2490 \approx \%24.90 \]

Görüldüğü gibi hesaplaması oldukça basit. Gelin bunu manuel hesaplamak yerine bilimsel hesap makinemizde hesaplayalım.

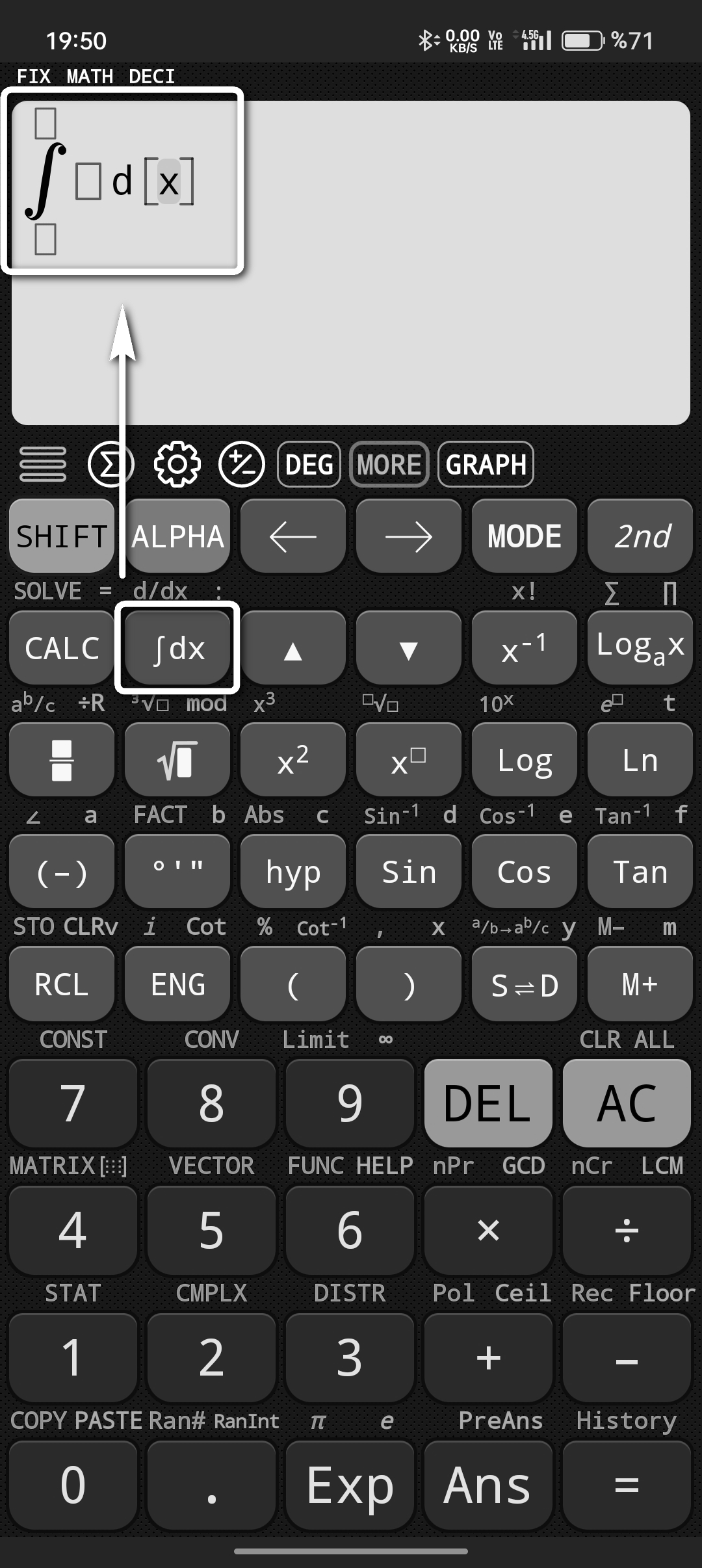
Öncelikle hesap makinemizde integral simgesinin olduğu tuşa basmalıyız.

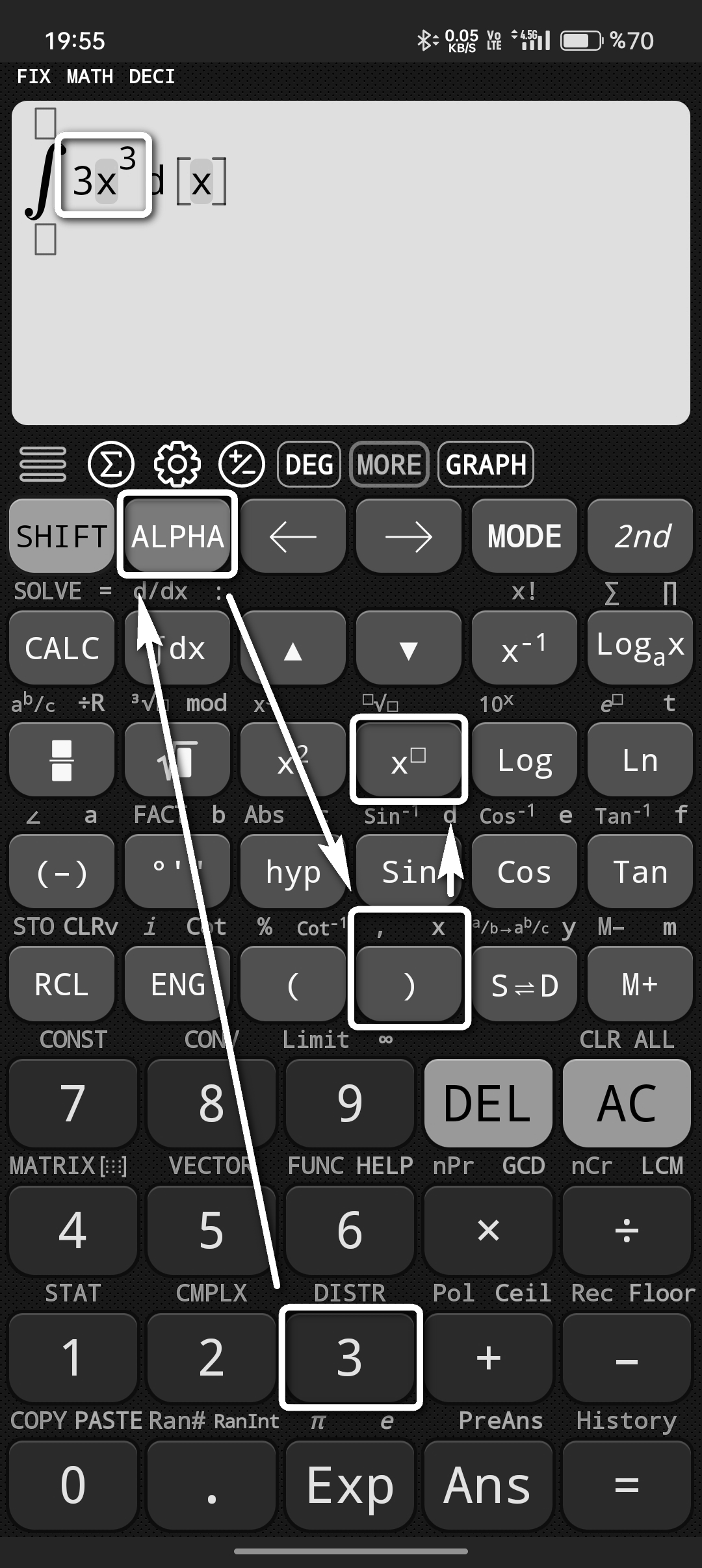
Ardından 3 yazıp ALPHA tuşuna basıyoruz. ) (parantez kapama) tuşunu seçiyoruz. Dikkat ederseniz ALPHA tuşunun rengi eflatun. Parantez kapama tuşunun sağ üsttünde eflatun renginde bir x harfi var. x yazabilmek için ALPHA'yı kullanıyoruz. x yazdıktan sonra son olarak x üzeri tuşuna basıyoruz ve 3 yazıyoruz.

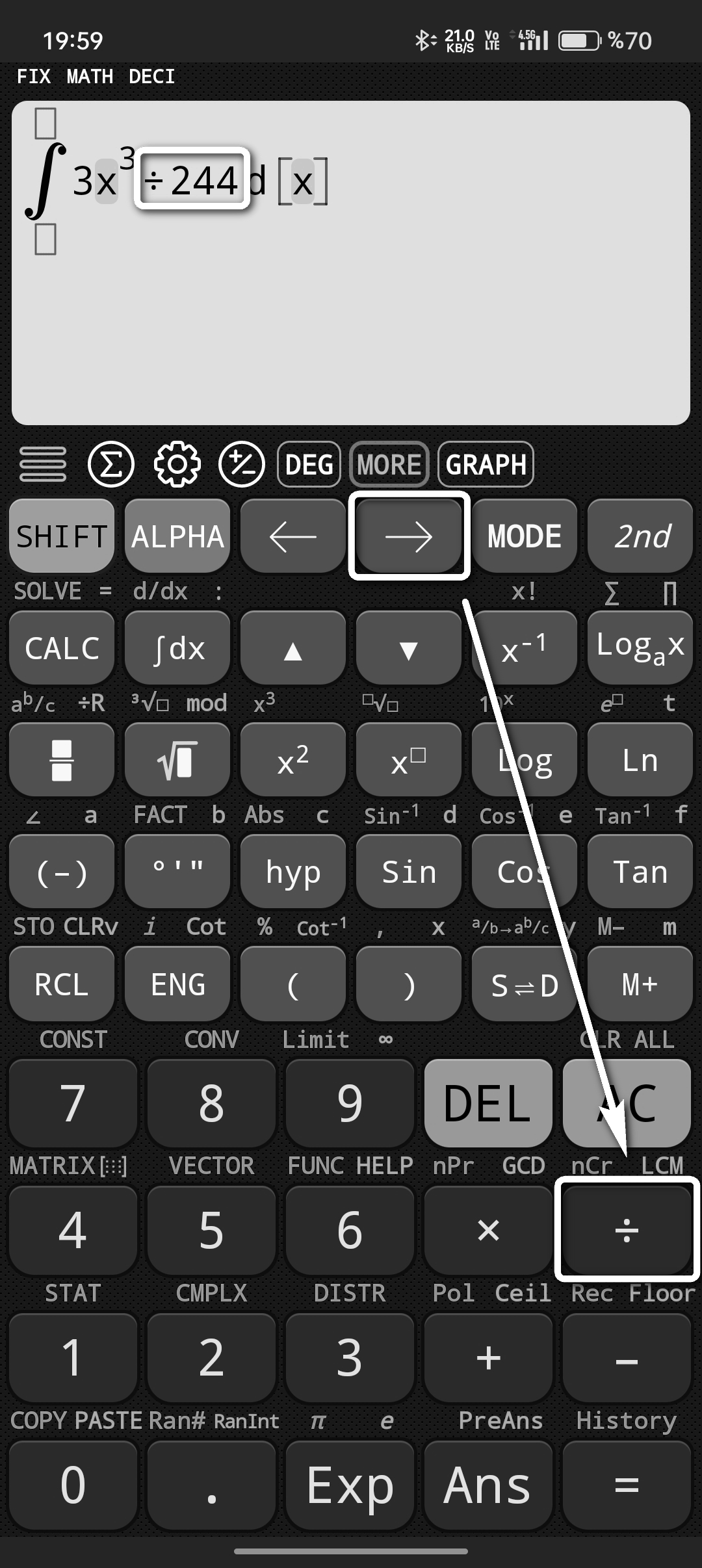
Üzeri ifadesinden çıkabilmek için sağa bakan ok tuşuna basıyoruz ve fonksiyonun geri kalan kısmını yazıyoruz.

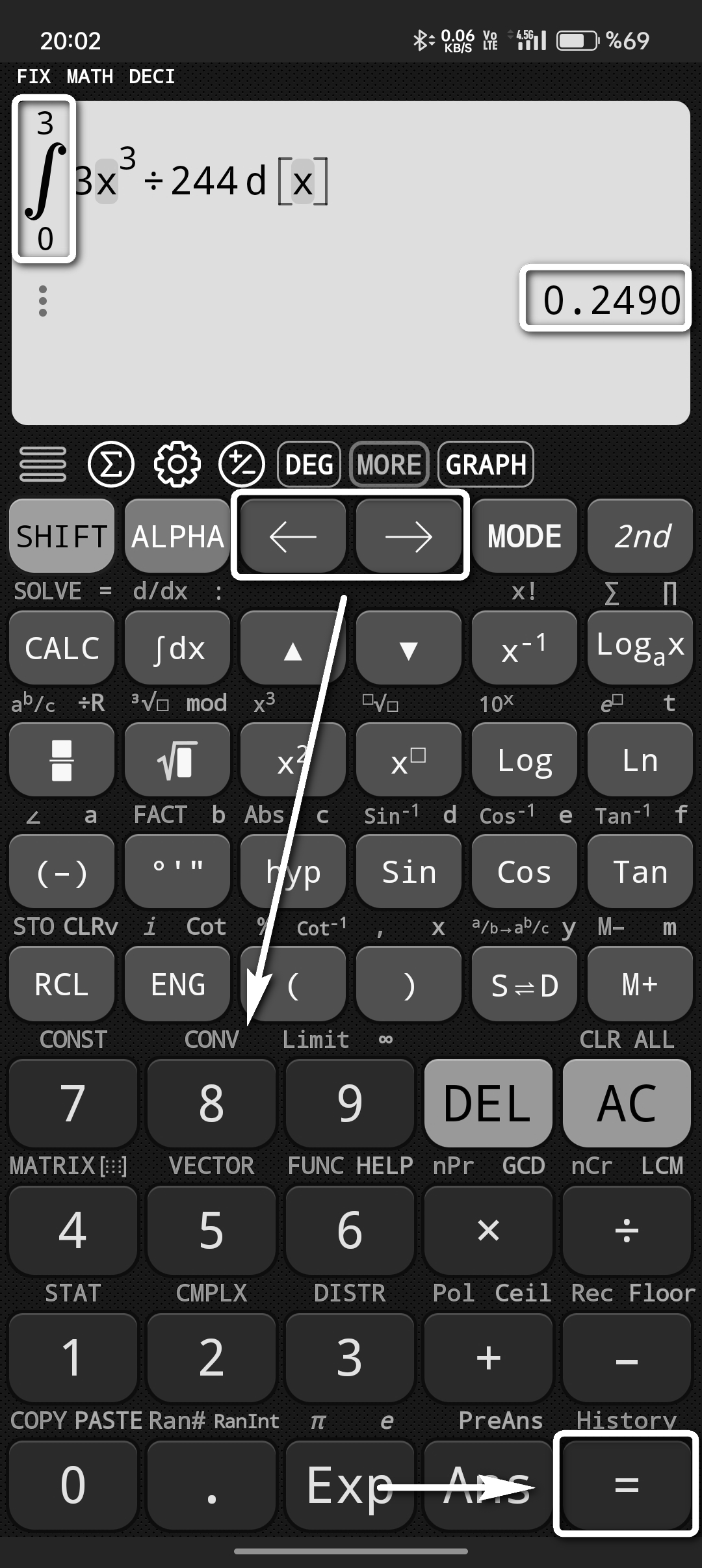
Son olarak integral sınırlarını içeren kutucuklara sağa ya da sola bakan yön tuşlarını kullanarak gidebiliriz. Bunları yazdıktan sonra eşittir dediğimizde sonuç 0.2490 olarak görüntülenecektir.

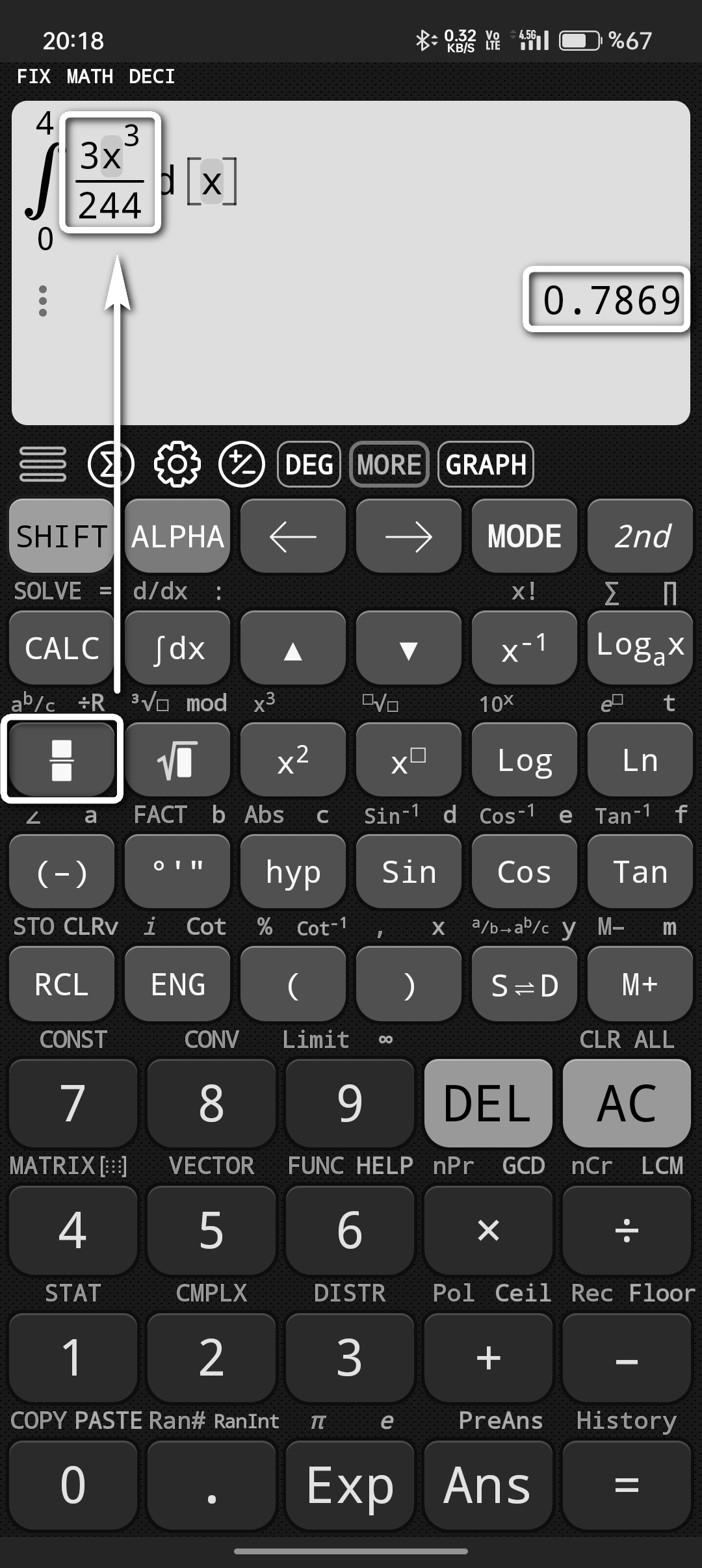
Eğer 3 yerine 4 senede bitirme olasılığı sorulsaydı sonuç %78.69 olacaktı. Dilersek en başta geleneksel gösterim şekli olan kesirli ifade tuşunu da kullanabiliriz.

Aynı hesaplamaları Casio fx-991EX hesap makinesinde de yapabilirsiniz.

Kesikli Dağılımlar

Bazı kesikli rassal değişkenleri özel modellerle bulmaya yarayan dağılımlara kesikli dağılım denir.

Bernouilli Dağılımı
Binom Dağılımı
Multinominal Dağılım
Geometrik Dağılım
Pascal Dağılımı
Hipergeometrik Dağılım
Poisson Dağılımı

şeklinde giden birçok dağılım bulunmaktadır. Bu dağılımların her birini tek tek incelemek yerine binom ve poisson dağılımlarına değineceğiz.

Binom Dağılımı

Anlatılmadı fakat yine de belirtelim. Binom dağılımı, bernouilli dağılımının özel bir halidir. Aslında birden çok kez tekrarlanan bernouilli dağılımı elde edilen bir dağılımdır. Bir deneyin n defa tekrarlanması sonucu olası iki sonuçtan birinin olasığını hesaplamamıza yarar.

\[ \begin{equation} f(x) = \begin{cases} \left(\matrix{\text{n} \\ \text{x}} \right) p^x (1-p)^{n-x} \\ \\ \text{0 diger durumlarda} \end{cases} \end{equation} \]

matematiksel gösterimidir.

Örneğin; bir torbada 7 kırmızı, 3 mavi top vardır. Yerine koyarak 5 top çekildiğinde toplardan 2'sinin mavi olma olasığı nedir?

Dikkat ederseniz kırmızı ve mavi olmak üzere 2 olasılığımız var. Topları yerine koyarak aynı deneyi 5 kez tekrarlıyoruz. Bu nedenle binom dağılımı kullanmalıyız.

Toplam 10 top vardır. Tek bir çekimde kırmızı gelme olasığı 7/10, mavi gelme olasılığı 3/10'dur.

\[ P(X=2) = \left(\matrix{\text{5} \\ \text{2}} \right) {\left(\matrix{3 \over 10} \right)}^2 {\left(\matrix{7 \over 10} \right)}^{5-2} \] \[ = \left(\matrix{\text{5} \\ \text{2}} \right) \left(\matrix{ 9 \over 100 } \right) \left(\matrix{ 343 \over 1000 } \right) \] \[ = { { 5 \cdot 4 \cdot 3 \cdot \cancel{2!} } \over \cancel{2!} 2! } \left(\matrix{ 9 \over 100 } \right) \left(\matrix{ 343 \over 1000 } \right) \] \[ \approx 0.3087 \approx \%30.87 \]

Sonuç olarak 5 toptan 2'sinin mavi gelme olasılığı %30.87'dir diyebiliriz.

hesap makinesinde binom dağılımı hesaplama

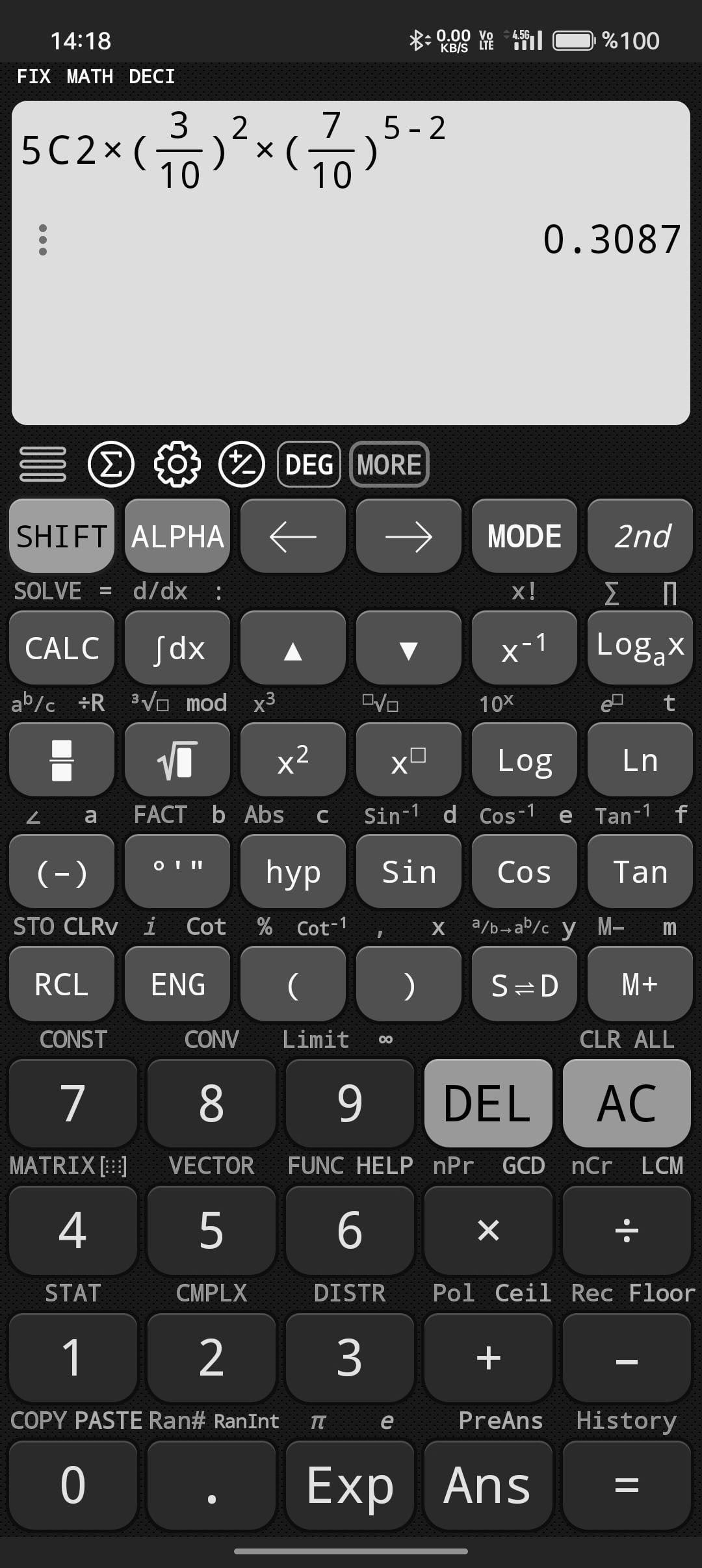
Sorunun çözümünü bilimsel hesap makinelerimizde hızlı bir şekilde hesaplayabiliriz.

Poisson Dağılımı

İstatistikçiler tarafından en sevilen dağılımlardan biridir. Veri sayısının (n) büyümesi ve olasılık değerinin (p) küçülmesi sonucu belirli bir zaman aralığında meydana gelen olayların olasılığını bulmak için kullanılır. Zaman aralığı burada kritik kavramdır.

\[ \begin{equation} f(x) = \begin{cases} \ { { \mathscr{e}^{-\lambda} {\lambda}^{x} } \over x!} \text{ $ \ \ x = 0, 1, 2, ... $ } \\ \\ \ \text{ $ \ \ $ } \text{0 diger durumlarda} \end{cases} \end{equation} \]

formülüdür. Burada e harfi euler (yuler) sabitidir. λ ise lambda okunur.

Örneğin; bir caféye sabah 9 ve 10 saatleri arası günde ortalama 4 müşteri gelmektedir. Herhangi bir günde bu saat aralığında 3'ten az müşteri gelme olasılığını bulunuz.

Soruda 3'ten az dediği için P(0), P(1) ve P(2) olasılıklarını hesaplamalıyız. Yani hiç müşteri gelmeme olasılığı ile 1 ve 2 müşteri gelme olasılıklarının toplamı sonucu verecektir.

λ = 4 ve x = 0, 1 ya da 2'dir. Formülü uyguladığımızda

Hiç müşteri gelmeme olasılığı:

\[ P(x) = { { \mathscr{e}^{-\lambda} {\lambda}^{x} } \over x! } \] \[ P(0) = { { \mathscr{e}^{-4} {4}^{0} } \over 0! } = 0.0183 \] \[ P(1) = { { \mathscr{e}^{-4} {4}^{1} } \over 1! } = 0.0733 \] \[ P(2) = { { \mathscr{e}^{-4} {4}^{1} } \over 2! } = 0.1465 \] \[ P(X \lt 3) = P(0) + P(1) + P(2) \approx 0.2381 \approx \%23.81 \]

3'ten az müşteri gelme olasılığı %23.81'dir diyebiliriz.

hesap makinesinde poisson dağılımı hesaplama

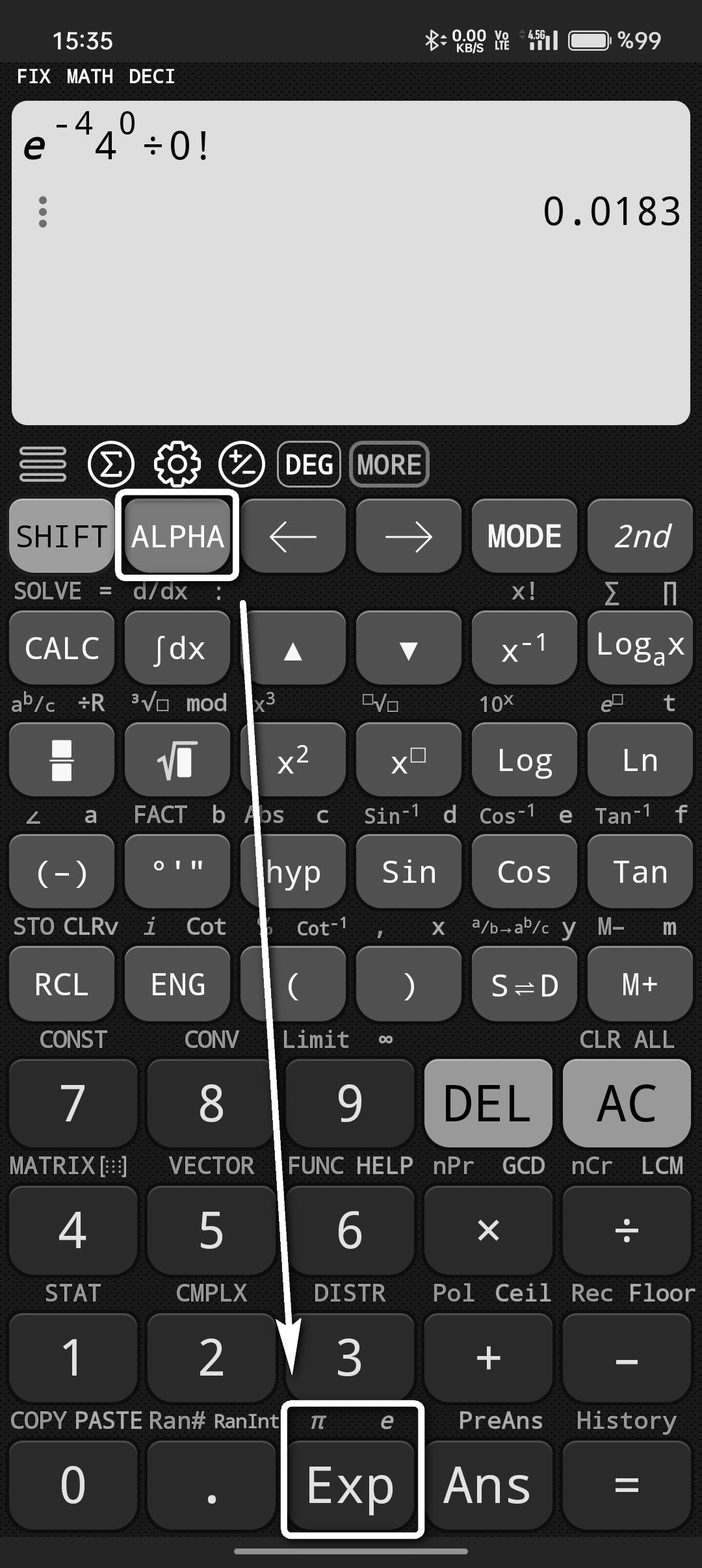
Hesap makinelerimizde poisson dağılımını hesaplarken e euler sabitini yazmak için ALPHA tuşuna bastıktan sonra Exp tuşunu seçebiliriz. Exp tuşunun sağ üsttünde eflatun renkli e sabitini görebilirsiniz. Bu nedenle ALPHA tuşunu kullanıyoruz.

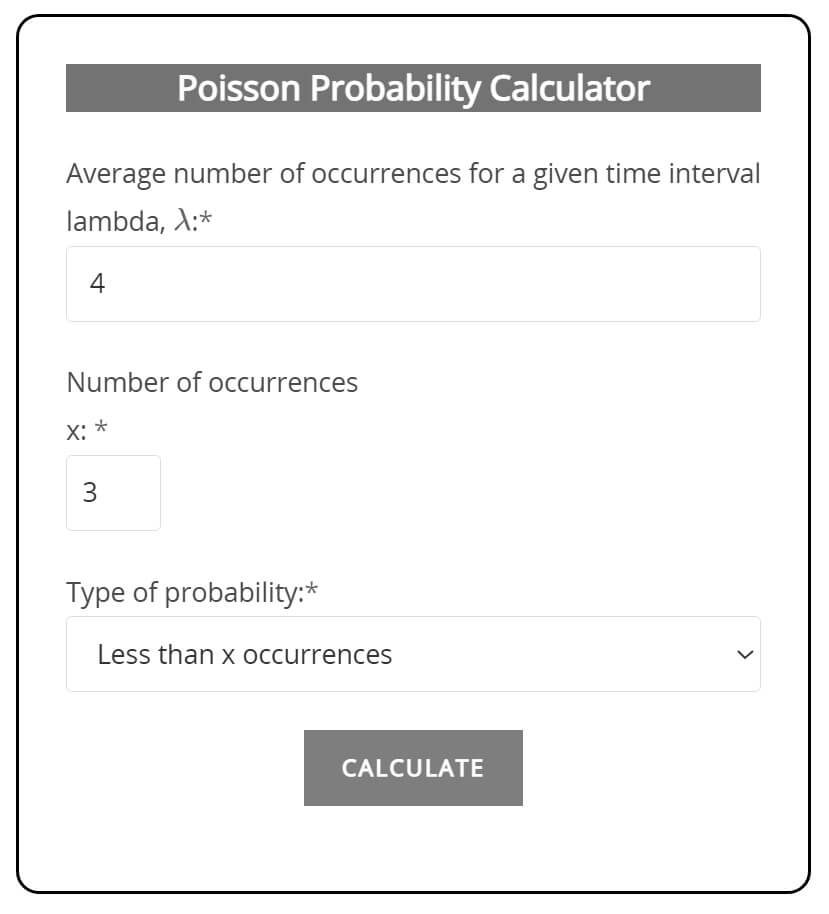
Bu tür soruları aynı zamanda statisticshelper.com gibi sitelerde de çözebiliriz.

Sonuç aynı olacaktır. Bu şekilde sadece lamdba ve x değerlerini girip çok daha hızlı sonuçlar elde edebiliriz.

Aynı soruyu ChatGPT'ye de sorabilirsiniz. ChatGPT çözümü de aynı olacaktır. Yapay zekâ yazılımlarının avantajı öğretici bilgiler de içermesidir.

Görüldüğü gibi soruyu günümüz teknolojisi ile birden çok yöntemle çok kısa bir sürede çözebiliriz.

Excel’de poisson dağılımı hesaplamak için
=POISSON.DAĞ(x-1;λ;DOĞRU) formülünü kullanabiliriz.

Sürekli Dağılımlar

Kesikli değişkenler belirli değerleri alabilirken, sürekli değişkenlerin belirli bir aralıktaki tüm değerleri alabildiğinden söz etmiştik. Sürekli rassal değişkenlerin belirli bir aralıktan bulunma olasılığı ile ilgilenen dağılımlara sürekli dağılım denir.

Normal Dağılım
Düzgün Dağılım
Üssel Dağılım

olmak üzere 3 farklı sürekli dağılım vardır. Biz bunların tamamını öğrenmek yerine bir sonraki derste normal dağılımı ve normal dağılımdan türetilen standart normal dağılımın ne olduğunu ve nasıl kullanıldığını detaylıca inceleyeğiz.

Dilerseniz sayfanın en altında yer alan "Sonraki Konu" düğmesine tıklayabilir ya da önce bu derste öğrendiklerinizi pekiştirmek amacıyla hemen aşağıdaki uygulamaları çözebilirsiniz.

Sıra Sizde

Uygulama: Tıp bölümünü 6 yılda bitirmenin olasılık yoğunluk fonksiyonu aşağıdaki gibidir.

\[ \begin{equation} f(x) = \begin{cases} {7x^2 \over 366} = {0 \leq x \leq 6}\\ \\ \ \text{ $ \ \ $ } \text{0 diger durumlarda} \end{cases} \end{equation} \]

Bir öğrencinin tıp bölümünü 5 yıl ya da 5 yıldan az bitirme olasılığı nedir?

Yanıtı Göster

\[ P(0 \leq x \leq 5) = \int_0^5 {7x^2 \over 366} dx = \left.{7x^3 \over 366 \cdot 3} \right\vert_{0}^{5} \] \[ P(5) = {7\cdot5^3 \over 366 \cdot 3} \approx 0.7969 \] \[ P(0) = {7\cdot0^3 \over 366 \cdot 3} \approx 0.0000 \] \[ P(5) - P(0) = 0.7969 - 0.0000 \approx 0.7969 \approx \%79.69 \]

Sonuç olarak öğrencinin tıp fakültesini 5 yılda bitirme olasılığı %79.69'dur.

Sorunun yanıtı ChatGPT'de de aynı olacaktır.

Uygulama: Bir banka şubesine bir saatte gelen ortalama müşteri sayısı 36'dır. Bu şubeye herhangi bir saatte 30'dan fazla müşteri gelme olasılığı kaçtır?

Yanıtı Göster

Soru poisson dağılımı ile çözülebilir. Manuel hesaplamaya çalışırsak sorunun aslında çok uzun bir yanıtı olduğunu görebiliriz. Bu nedenle statisticshelper.com sitesinden yardım alıyoruz.

30'dan az müşteri gelme olasılığını 1'den çıkarırsak 30'dan fazla müşteri gelme olasılığını buluruz. 30'dan az müşteri gelme olasılıkları P(0) + P(1) + P(2) + ... + P(28) + P(29) olasılıklarının toplamıdır ve %18.06'ya eşittir.

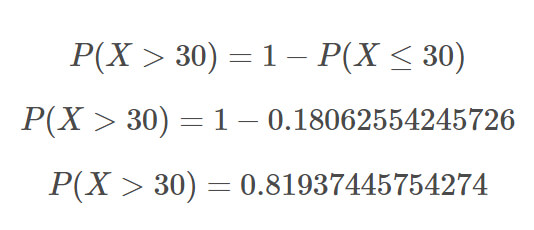
Bu toplamı 1'den çıkardığımızda sonuç %81.94 olacaktır.

Evet hepsi bu kadar. Şimdi normal dağılım konusuna geçebiliriz.

<<< Önceki Konu

Sonraki Konu >>>