İstatistik derslerini tablet üzerinden çalışmanız şiddetle tavsiye olunur.
Momentler, Çarpıklık ve Basıklık
Momentler, çarpıklık (asimetri) ve basıklık bir serinin ortalamaya göre nasıl dağıldığını belirlemek için kullanılan temel istatistik ölçüleridir.
Moment
Terimlerin sıfırdan veya aritmetik ortalamadan sapmalarının çeşitli kuvvetlerine moment1 adı verilmektedir. Moment, bir serideki gözlem değerlerinin sıfırdan veya aritmetik ortalamadan farklarının kuvvetlerinin aritmetik ortalamasıdır.
İleri Okuma
Matematikte Momentler
Matematik bilimi içinde moment kavramı fizik bilimi için ortaya çıkartılmış olan moment kavramından geliştirilmiştir. Bir bir reel değişkenin reel-değerli fonksiyon olan f(x)’in c değeri etrafında (n)inci momenti şöyle ifade edilir:
Sıfır değeri etrafında olan momentler en basit olarak bir fonksiyonun momenti diye anılır.
Olasılık kuramı ve istatistik bilim dalları için momentlerin ilgili olduğu fonksiyonlar bir rassal değişken için olasılık yoğunluk fonksiyonu ile ilgilidir. Bir olasılık yoğunluk fonksiyonun sıfır etrafındaki (n)inci momenti X’nin matematiksel beklentisidir. Ortalama μ etrafındaki momentler merkezsel momentler olarak adlandırılır. Bunlar bir fonksiyonun şeklini betimlerler.
Bir rassal değişken olan X’in olasılık dağılımının (n)inci merkezsel momenti şudur:
Böylece birinci merkezsel moment 0 olur.
İkinci merkezsel moment varyans σ2 olur; bunun pozitif kare kökü standart sapma σ olur.
Momentler 2 gruba ayrılır:
- Sıfıra Göre Momentler
- Aritmetik Ortalamaya Göre Momentler
Sıfıra Göre Momentler
Anakütle Sıfıra Göre Momentleri
Örneklem Sıfıra Göre Momentleri
m: Sınıf Orta Sayısı, f: Frekans
M1: 1. Dereceden Moment, M4: 4. Dereceden Moment, Mr: r. Dereceden Moment
Aritmetik Ortalamaya Göre Momentler
Anakütle Aritmetik Ortalamaya Göre Momentleri
Örneklem Aritmetik Ortalamaya Göre Momentleri
m: Sınıf Orta Sayısı, f: Frekans
M1: 1. Dereceden Moment, M4: 4. Dereceden Moment, Mr: r. Dereceden Moment
König Teoremi
Sıfıra göre momentler biliniyorsa, aritmetik ortalamaya göre momentler kolaylıkla hesaplanabilir. König Teoremi adı verilen momentler arasındaki ilişki şu şekildedir:
Uygulama: Aşağıda 7 değerden oluşan x serisi verilmiştir.
x = 10, 12, 14, 14, 16, 18, 20
Serinin 1’den 4. Dereceye kadar olan momentlerini sıfıra, aritmetik ortalamaya ve König Teoremine göre bulunuz.
Sıfıra göre momentler:
Aritmetik ortalamaya göre momentler:
x̄ = 15
König Teoremine göre momentler:
Çarpıklık
Asimetri ya da Çarpıklık (Skewness) seri değerlerinin başta mı yoksa sonda mı yoğunlaştığını tespit etmemize yarayan istatistik ölçüsüdür.
Serileri incelediğimizde her seri aynı özelliğe sahip olmayabilir. Örneğin ortalaması ve standart sapması eşit olan iki seriden birindeki değerler başlangıç değerleri etrafında yoğunlaşırken ikinci serideki değerler son değerler etrafında yoğunlaşabilir. Bu şekilde serilerin simetrik dağılıp dağılmadığına bakarız. Seriler simetrik dağılmadığında adına asimetrik dağılım (skewed distribution, asymmetrical distribution) deriz.2
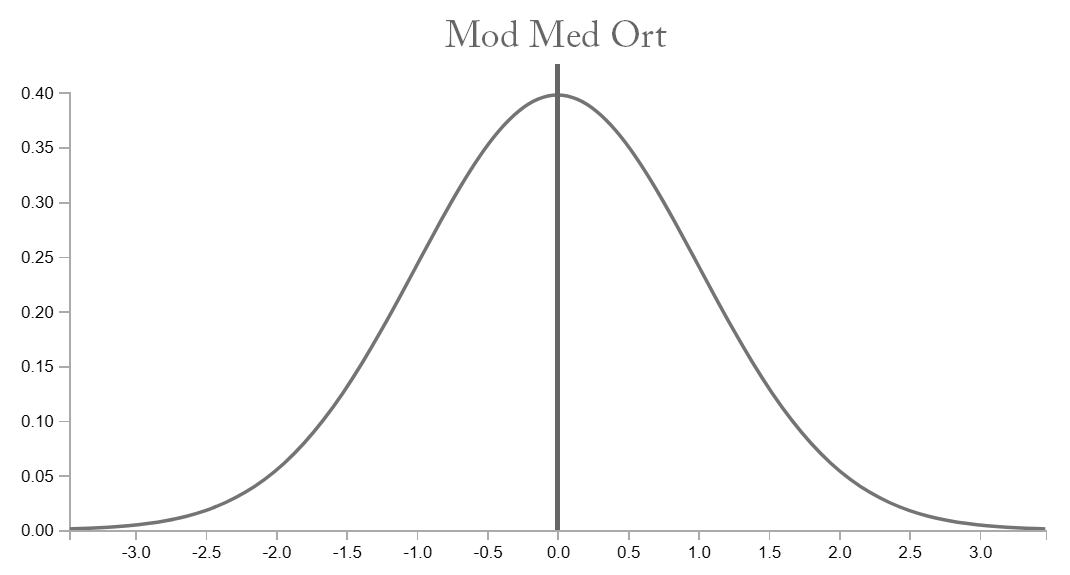
Simetrik dağılımlarda Mod = Medyan = Ortalama birbirine eşittir. Normal dağılım, simetrik dağılıma en iyi örnektir.
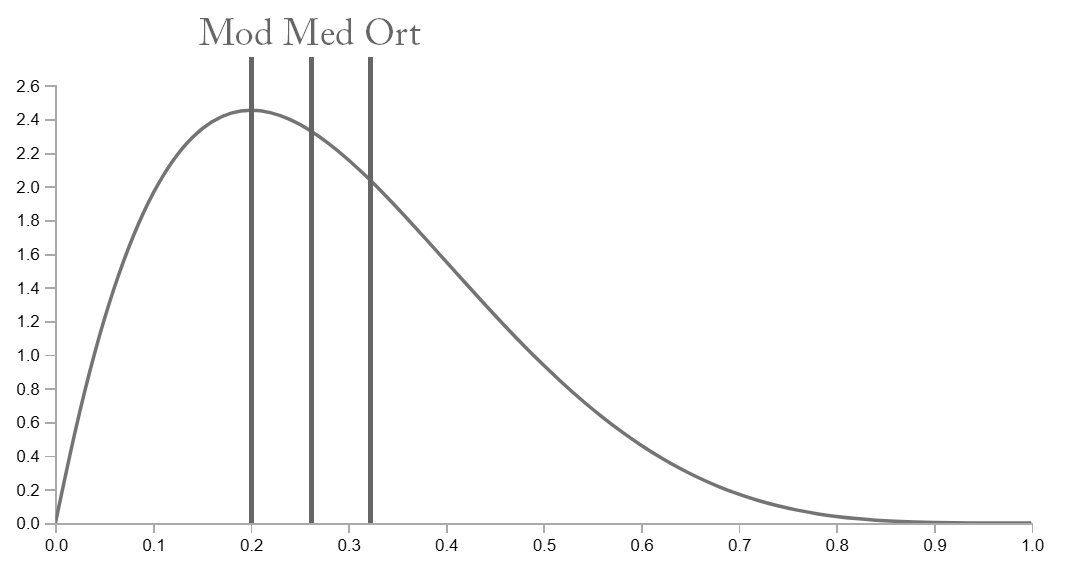
Pozitif asimetrik dağılımlarda Mod > Medyan > Ortalama ilişkisi vardır. Bu dağılımlar aynı zamanda “sağa çarpık” olarak adlandırılır.
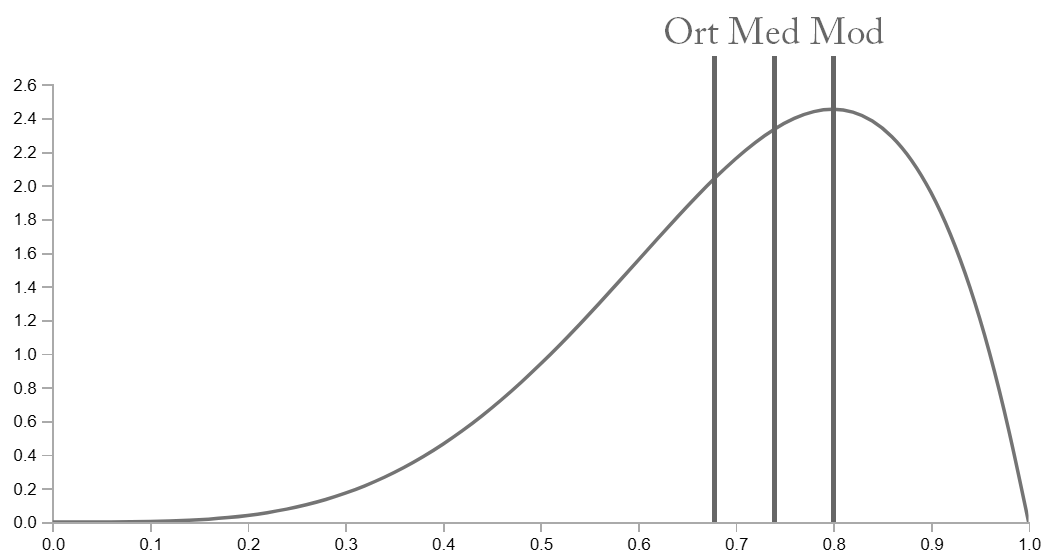
Negatif asimetrik dağılımlarda Ortalama > Medyan > Mod ilişkisi vardır. Bu dağılımlar aynı zamanda “sola çarpık” olarak adlandırılır.
Tam simetrik ya da tam simetriğe yakın serilerde şu ilişki vardır:
x̄: Aritmetik Ortalama, x̃: Medyan
Çarpıklık (Asimetri) Ölçüleri
Çarpıklık ölçüleri
- Ortalamaya Dayanan Asimetri Ölçüsü (Pearson Asimetri Ölçüsü)
- Kartillere Dayanan Asimetri Ölçüsü (Bowley Asimetri Ölçüsü)3
- Momentlere Dayanan Asimetri Ölçüsü
olmak üzere 3’e ayrılır.
Pearson Asimetri Ölçüsü
x̄: Aritmetik Ortalama, x̃: Medyan, s: Standart Sapma
Ortalamaya dayanan asimetri ölçüsüdür. -3 ve +3 arasında değer alır. 0’ın altında olduğu durumlarda sola çarpık negatif asimetrik dağılımdan, 0’ın üzerinde olduğu durumlarda ise sağa çarpık pozitif asimetrik dağılımlardan söz edilir. Tam simetri durumunda 0 değerini verir.
Bowley Asimetri Ölçüsü
Kartillere dayanan asimetri ölçüsüdür. -1 ve +1 arasında değer alır. 0’ın altında olduğu durumlarda sola çarpık negatif asimetrik dağılımdan, 0’ın üzerinde olduğu durumlarda ise sağa çarpık pozitif asimetrik dağılımlardan söz edilir. Tam simetri durumunda 0 değerini verir.
Momentlere Dayanan Asimetri Ölçüsü
Momentler yardımıyla hesaplanan bu çarpıklık ölçüsünde sonuç 0’dan küçükse sola çarpık negatif asimetrik dağılımdan, 0’dan büyükse sağa çarpık pozitif asimetrik dağılımdan söz edilir. Tam simetri durumunda 0 değerini verir.
Aritmetik ortalamaya göre 3. dereceden moment asimetri ölçüsü olarak bilinir. Bu sebeple α3 ile gösterilir.
Uygulama: Aşağıda 12 değerden oluşan x serisi verilmiştir.
x = 10, 10, 11, 12, 12, 12, 12, 12, 12, 14, 16, 20
Serinin çarpıklığını Pearson, Bowley ve Momentlere Dayanan Asimetri ölçülerine göre yorumlayınız.
Pearson Asimetri Ölçüsüne göre öncelikle ortalama ve medyan değerleri bulunmalıdır.
1.00’a yakın pozitif bir asimetri ölçüsü söz konusudur. Bu sebeple hafif sağa çarpık pozitif asimetrik dağılımdan söz edilebilir.
Bowley Asimetri Ölçüsüne göre Q4 dışında tüm kartil değerleri bulunmalıdır.
Pearson Asimetri ölçüsünde olduğu gibi 1.00’a yakın pozitif asimetri söz konusudur. Bu sebeple hafif sağa çarpık pozitif asimetrik dağılımdan söz edilebilir.
Momentlere Dayanan Asimetri Ölçüsüne göre serinin 3. dereceden momentini bulmamız yeterlidir. Standart sapmayı Pearson Asimetri Ölçüsünde hesaplamıştık.
Bulunan asimetri ölçüsü 0’ın üzerinde olduğu için sağa çarpık pozitif asimetrik dağılımdan söz edilir. 3 asimetri ölçüsünde de seri değerlerinin pozitif asimetrik dağıldığı ve dağılım sağa çarpık olduğu sonucuna varılmıştır.
Basıklık
Basıklık (Kurtosis) seri değerlerinin ortalama etrafında ne kadar yoğunlaşıp yoğunlaşmadıklarının ölçüsüdür.
Ortalama etrafında yoğunlaşan seriler sivri bir görünüme sahip olup standart sapmaları düşüktür. Ortalamadan uzaklaşan seriler ise basık bir görünüme sahip standart sapmaları yüksektir. Normal dağılımlar ise ne sivri ne de basık bir görünüme sahiptir. Simetrik görünüm sergiler.
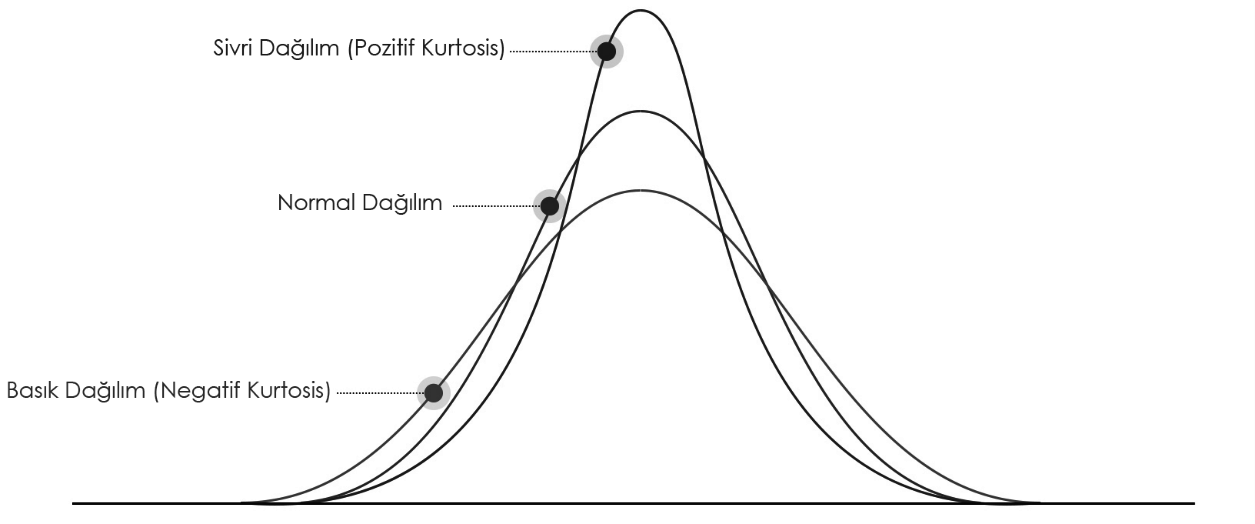
Aritmetik ortalamaya göre 4. dereceden moment, basıklık (kurtosis) ölçüsü olarak bilinir ve α4 ile gösterilir.
Basıklık ölçüsü 3’e eşitse seri normal yükseklikte, 3’ten küçükse seri basık, 3’ten büyükse serinin sivri olduğu söylenir. Özetle kurtosiste ölçünün 3’ten büyük olup olmamasına bakılır.
Uygulama: Aşağıda 12 değerden oluşan x = 10, 10, 11, 12, 12, 12, 12, 12, 12, 14, 16, 20 serisinin basıklık ölçüsünü hesaplayınız.
Basılık ölçüsünü bulabilmek için serinin 4. dereceden momentini ve standart sapmasını bulmamız yeterlidir.
Bulunan sonuç 3’ten büyük olduğu için serinin sivri bir dağılım sergilediği sonucuna ulaşılabilir.
SPSS'te Çarpıklık ve Basıklık
SPSS'te çarpıklık (skewness) ve basıklık (kurtosis) değerlerini hesaplamak basittir.
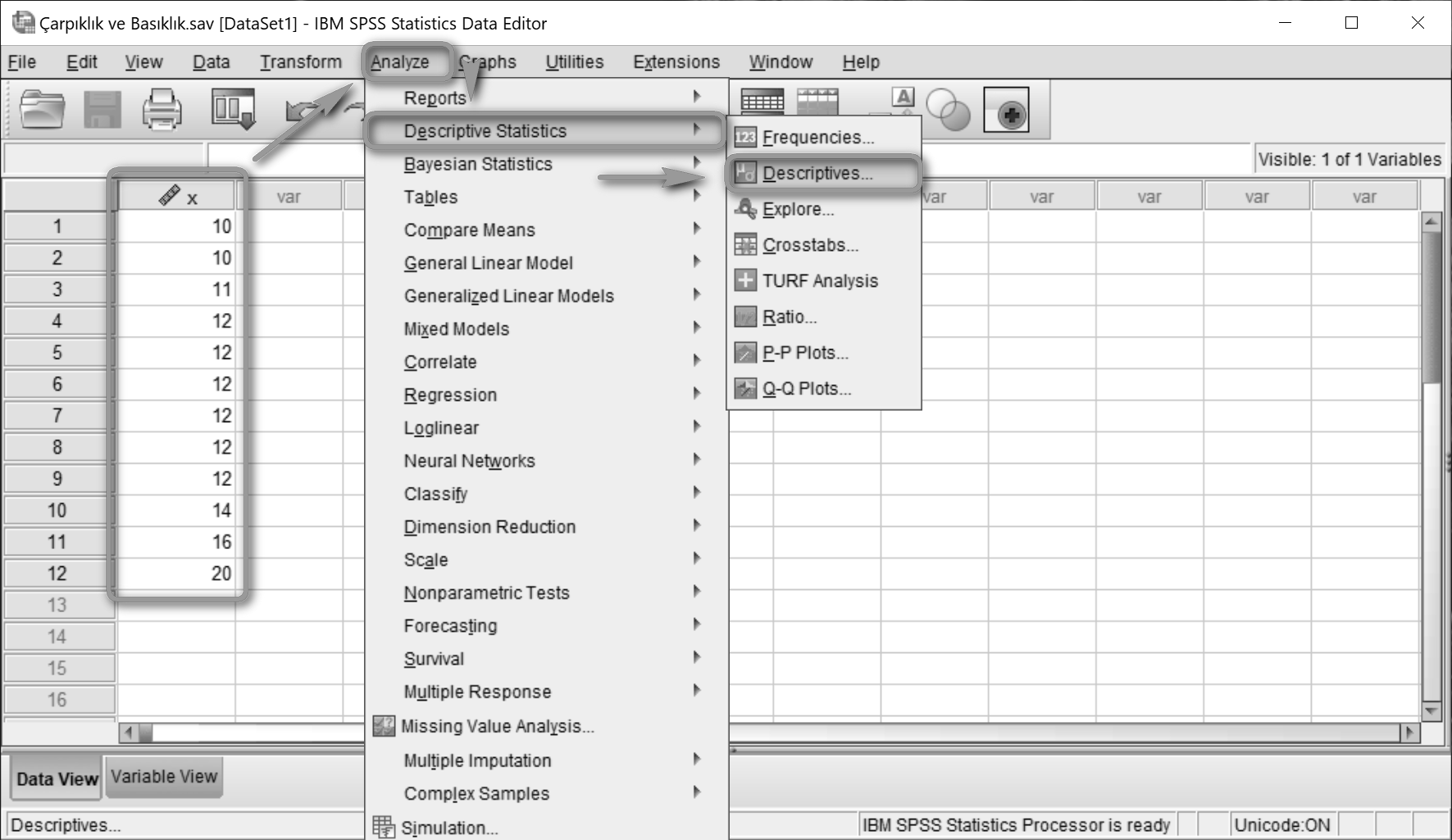
Seri değerleri girildikten sonra menüden Analyze > Descriptive Statistics > Descrpitives... yolu izlenir.
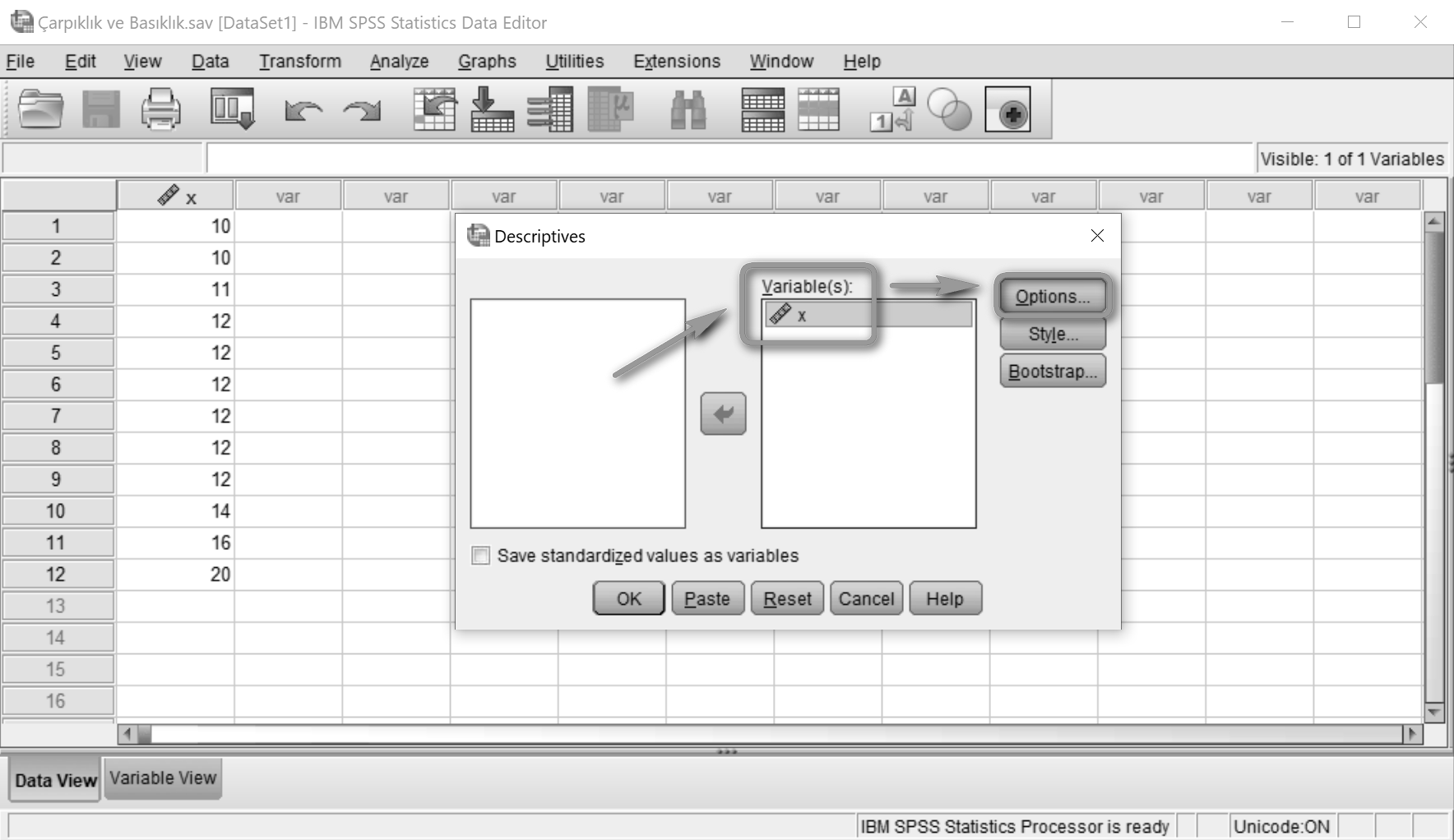
Değişken Variable(s) alanına aktarıldıktan sonra Options'a tıklanır.
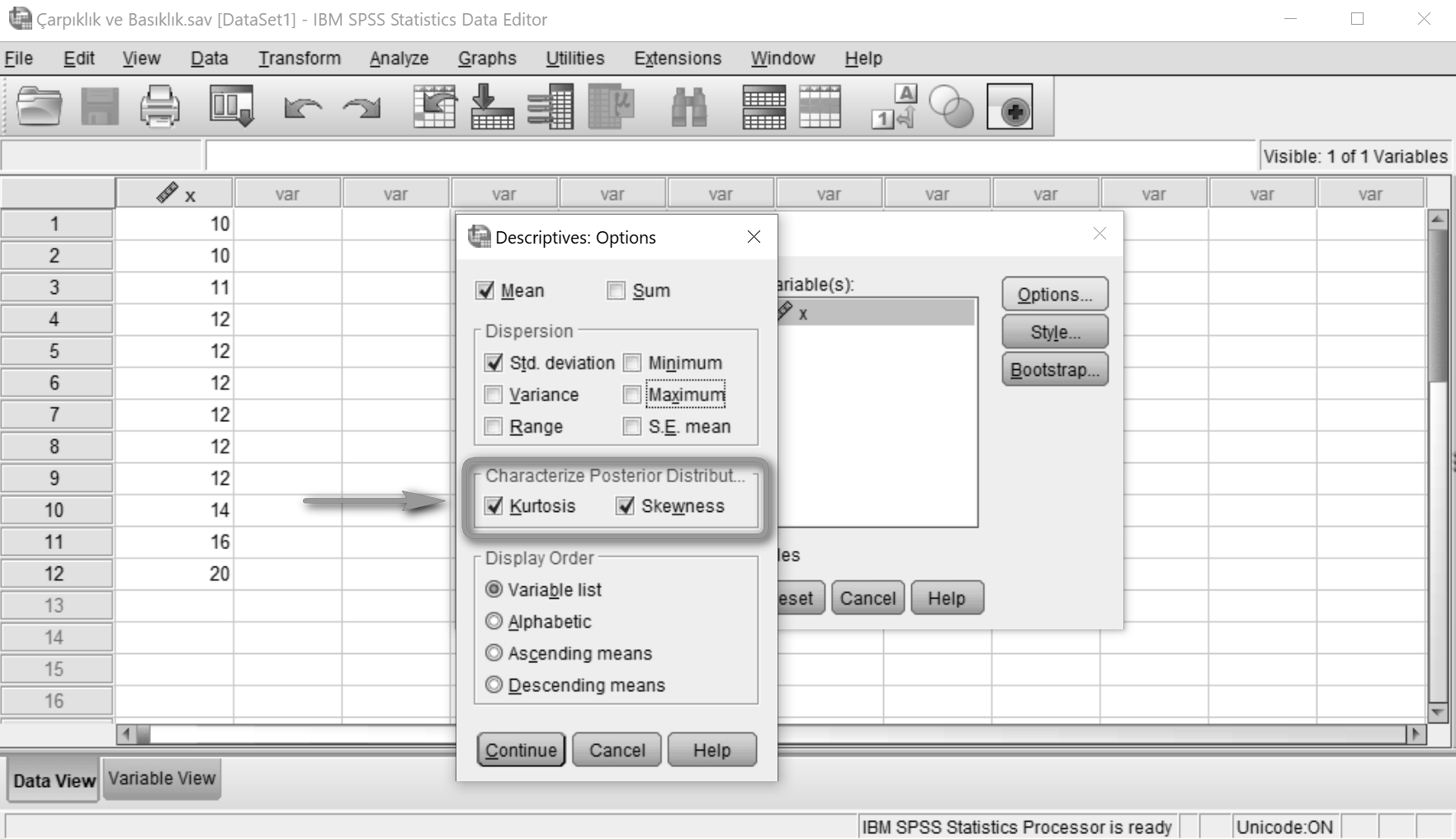
Açılan pencerede Kurtosis (Basıklık) ve Skewness (Çarpıklık) seçimleri yapılır. Continue'ya tıklanır.
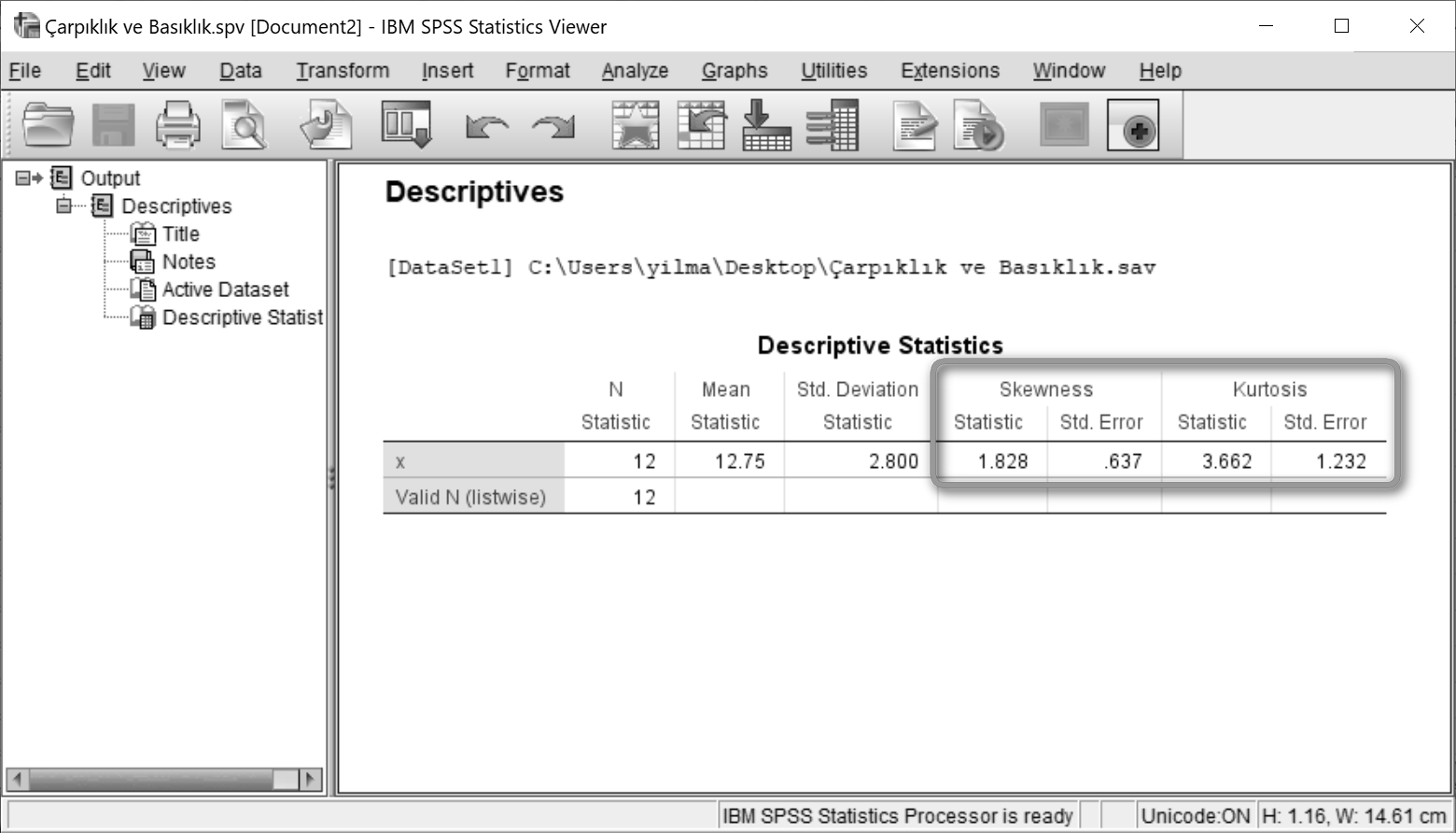
Çıktı alanında Skewness (Çarpıklık) ve Kurtosis (Basıklık) değerleri standart sapmaları ile birlikte listelencektir.
SPSS'in çarpıklık ve basıklık hesaplaması biraz önce öğrendiğimiz yöntemden farklıdır. SPSS çarpıklık ve basıklık değerlerini hesaplarken normalleştirme (normalization) yöntemini uygulamaktadır. Buna göre skewness (çarpıklık) değeri +1'den yüksekse sağa çarpık, -1'den azsa sola çarpık bir dağılım söz konusudur. Çarpıklık değeri -1 ve +1 arasında ise asimetriden söz edilmez. Aynı şekilde kurtosis (basıklık) değeri +1'den yüksekse leptokurtik olarak adlandırılan sivri uçlu dağılım, -1'den küçükse platykurtik olarak adlandırılan basık dağılım söz konusudur. Kurtosis -1 ve +1 arasında ise basık olmayan normal dağılımdan söz edilir. Örneğimizde skewness 1.828 hesaplanmıştır. +1'den büyük olduğu için seri sağa çarpık bir dağılım sergilemiştir. Kurtosis ise 3.662 hesaplanmıştır. Yine +1'den büyük olduğu için sivri uçlu dağılım söz konusudur. Sonuç olarak serimiz sağa çarpık sivri uçlu bir dağılımdır.
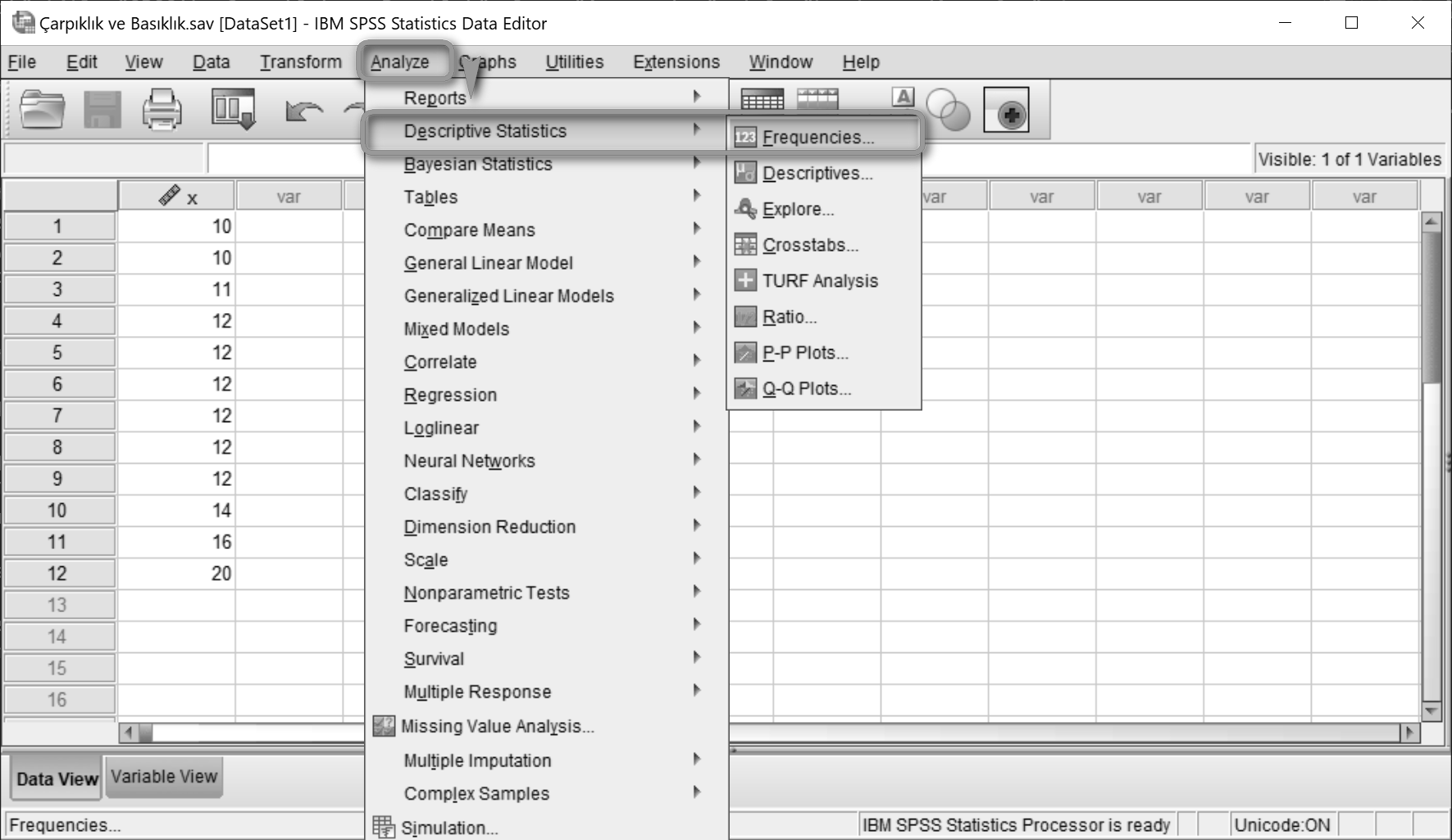
Eğer çarpıklık ve basıklık değerlerini grafikleştirmek istersek öncelikle menüden Analyze > Descriptive Statistics > Frequencies... yolunu izlemeliyiz.
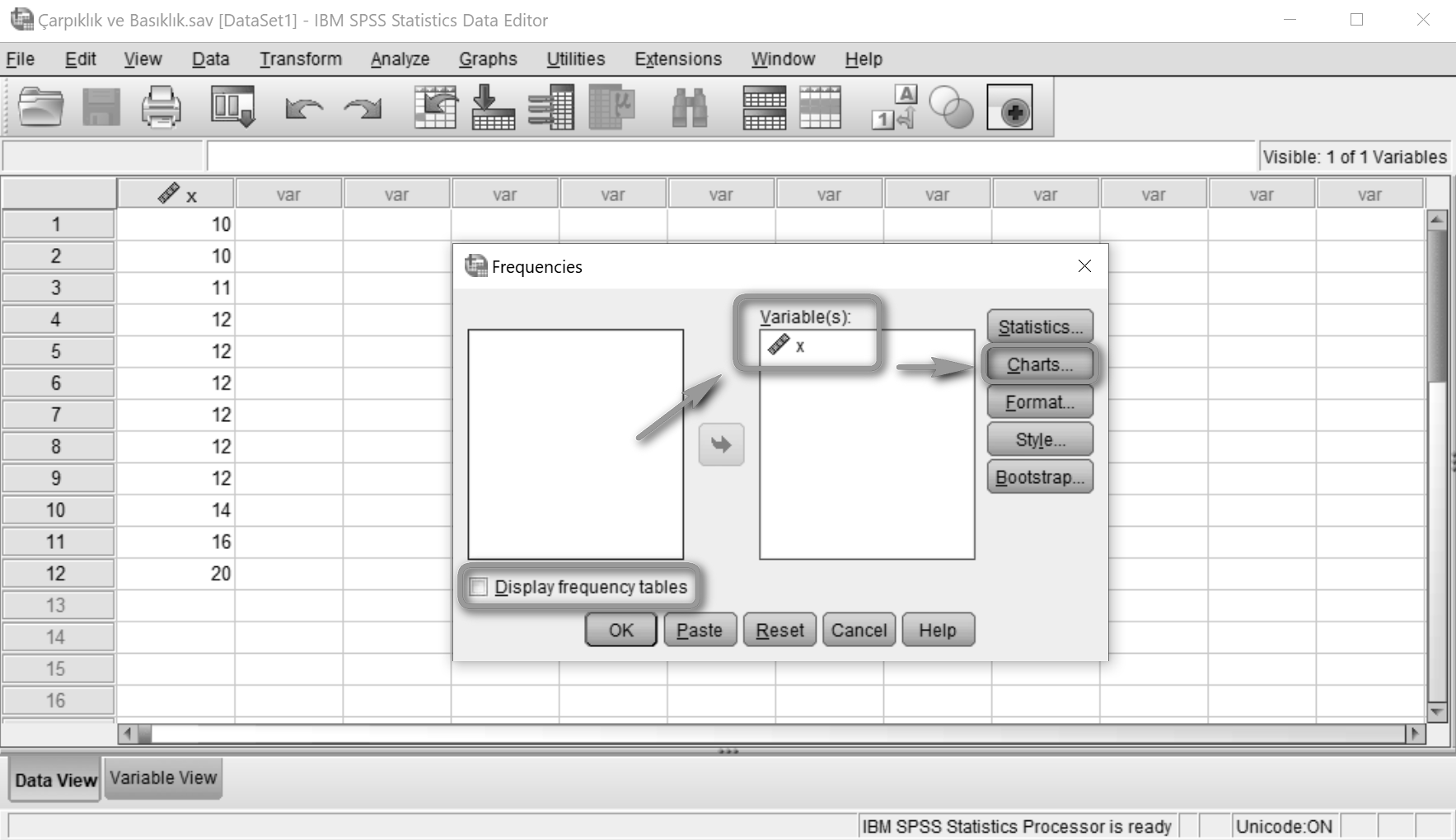
Display frequency tables seçeneğini kaldırdıktan sonra değişkenimizi Variable(s) alanına taşımalıyız. Ardından Charts düğmesine tıklıyoruz.
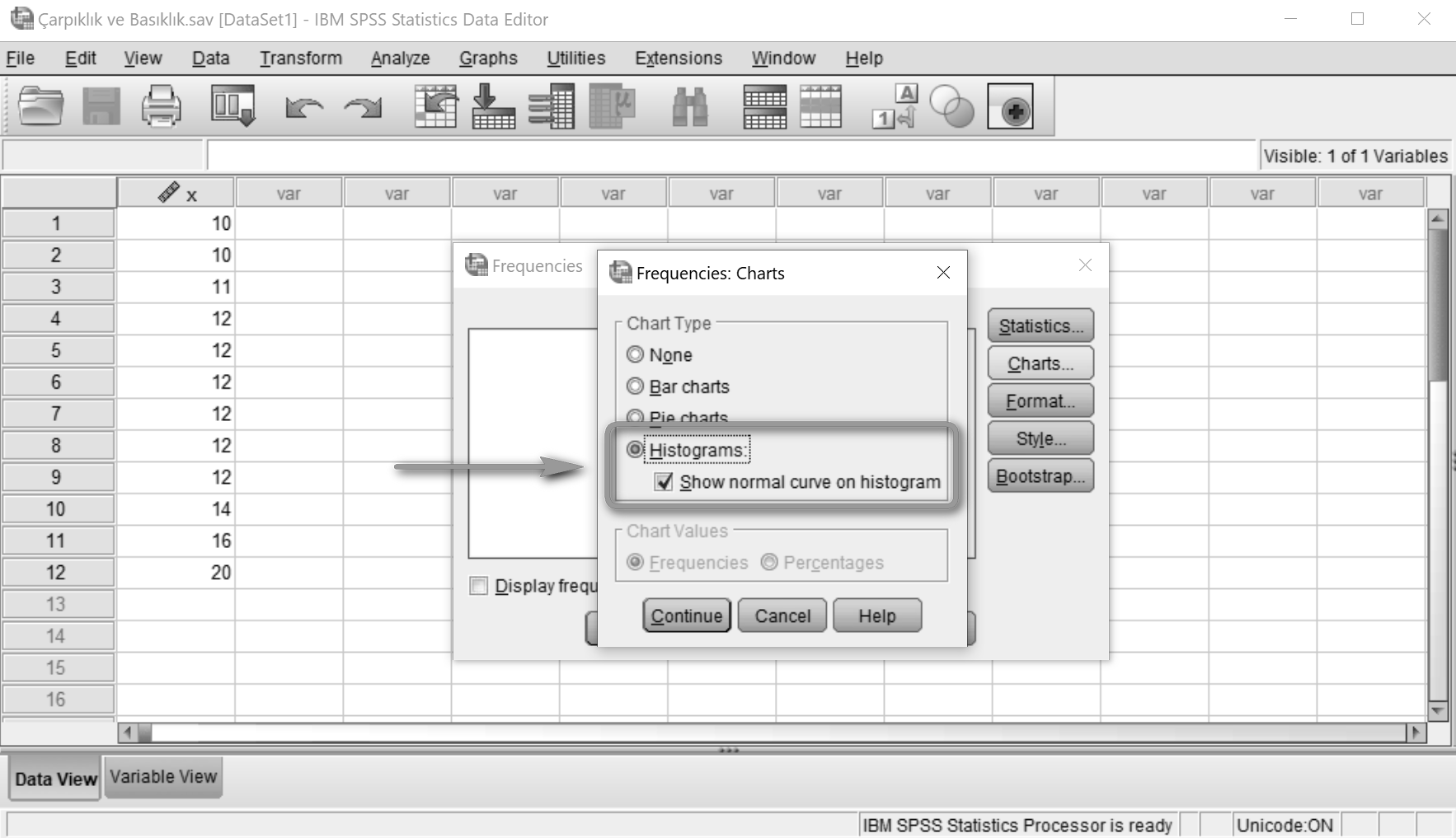
Açılan sayfada Histograms ve bir altındaki kutucuğu seçiyoruz. Continue'ya, ardından OK'a tıklıyoruz.
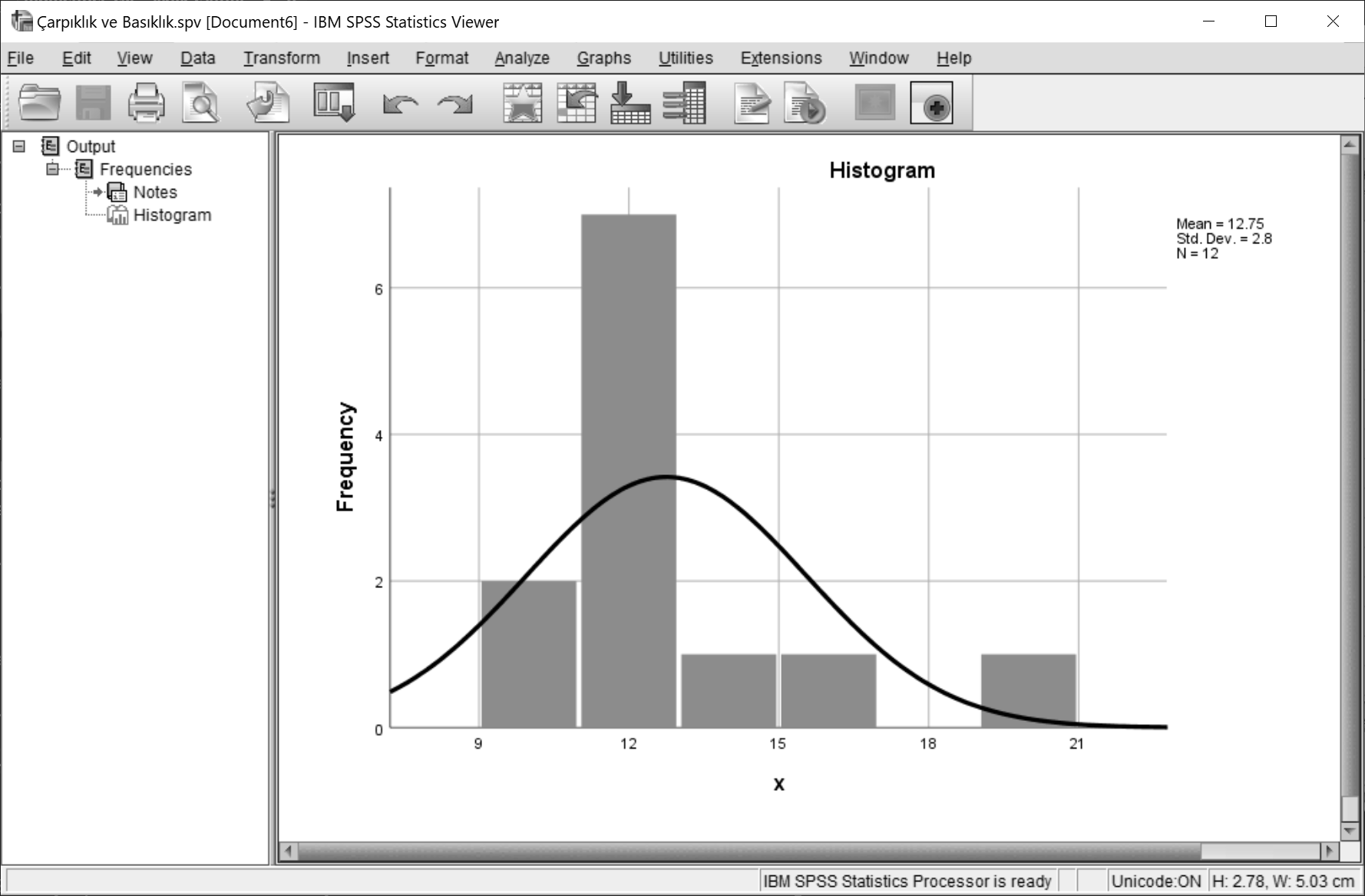
Çıktı penceresinde dağılımın sivri uçlu sağa çarpık bir dağılım olduğu teyit edilebilir. Gözlem değerlerimiz az olduğu için bu tür örneklerde çarpıklık ve basıklık net olarak görülemeyebilir. Buna rağmen gözlem değerleri, yani veri birimlerin sayısı arttıkça serinin çarpıklık ve basıklık durumu hakkında daha kapsamlı sonuçlara ulaşılabilir.
Sıra Sizde
Uygulama:
A serisinin
- Pearson Asitmeri Ölçüsü 2.2816
- Basıklık Ölçüsü 3.9614
B serisinin
- Pearson Asimetri Ölçüsü -1.2817
- Basıklık Ölçüsü 1.2419
bulunmuştur. İki serinin çarpıklık ve basıklık değerlerini yorumlayınız.
A serisinin Pearson Asimetri Ölçüsü 0'dan büyük olduğu için sağa çarpık pozitif asimetrik dağılım, Basıklık Ölçüsü 3'ten büyük olduğu için sivri uçlu dağılım sergilendiğinden söz edilebilir.
B serisinin Pearson Asimetri Ölçüsü 0'dan küçük olduğu için sola çarpık negatif asimetrik dağılım, Basıklık Ölçüsü 3'ten küçük olduğu için basık dağılım sergilendiğinden söz edilebilir.
2 Dağılım, simetrikse ve aykırı değerler yoksa aritmetik ortalama, asimetrikse ve aykırı değerler varsa medyan kullanımı tercih edilir.
3 Galton Asimetri Ölçüsü olarak da bilinir.