İstatistik derslerini tablet üzerinden çalışmanız şiddetle tavsiye olunur.

Merkezî Eğilim Ölçüleri

Veri kümesinin ortasını belirlemeye yönelik ölçülerin tümüne merkezî eğilim ölçüsü (measure of central tendency) denir. Adından da anlaşılacağı üzere amaç, veri setinin ne yöne doğru eğilim gösterdiğini tespit etmektir. Bu eğilimi tespit etmek içinse ortalamalar kullanılmaktadır.

Ortalama denilince birçoğumuzun aklına aritmetik ortalama gelmektedir. Fakat istatistikte geometrik ve harmonik ortalama, mod, medyan gibi kimi durumlarda daha anlamlı sonuçlar veren ortalamalar da bulunmaktadır.

Duyarlı ortalamalar serideki aykırı değerlerden etkilenirken duyarlı olmayan ortalamalar etkilenmemektedir.

Duyarlı Ortalamalar

Duyarlı Ortalamaların Karşılaştırılması

SPSS'te Duyarlı Ortalamalar

Duyarlı Olmayan Ortalamalar

SPSS'te Duyarlı Olmayan Ortalamalar

Aritmetik Ortalama

Aritmetik Ortalama (Arithmetic Mean), en bilinen ve en çok kullanılan ortalama türüdür. Seriyi oluşturan tüm değerlerin toplanıp gözlem sayısına bölünmesi ile bulunur.

Anakütlede µ (mü), örneklemde x̄ (x üzeri çizgi, x-bar) notasyonu kullanılır.

Σ toplamı, N ve n gözlem sayısını belirtir.

Anakütle Aritmetik Ortalaması

Basit Serilerde

\[ \mu = {\Sigma X_i \over N} \]

Frekans Serilerinde

\[ \mu = {\Sigma X_i f_i \over N} \]

Gruplandırılmış Serilerde

\[ \mu = {\Sigma m_i f_i \over N} \]

Örneklem Aritmetik Ortalaması

Basit Serilerde

\[ \bar x = {\Sigma x_i \over n} \]

Frekans Serilerinde

\[ \bar x = {\Sigma x_i f_i \over n} \]

Gruplandırılmış Serilerde

\[ \bar x = {\Sigma m_i f_i \over n} \]

m: Sınıf Orta Sayısı, f: Frekans

Excel’de aritmetik ortalama almak için
=ORTALAMA() formülünü kullanabiliriz.

Uygulama: Bir sınıftan seçilen 10 öğrencinin sınav notları aşağıda verilmiştir.

\[ x = 40, 55, 60, 60, 65, 70, 75, 80, 85, 90 \]

Notların aritmetik ortalamasını bulunuz.

\[ \bar x = {\Sigma x_i \over n} \] \[ \bar x = {40 + 55 + 60 + 60 + 65 + 70 + 75 + 80 + 85 + 90 \over 10} = 68 \]

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu

Öğrenci Sayısı

155 cm

160 cm

165 cm

170 cm

175 cm

180 cm

185 cm

190 cm

Toplam (Σ)

Boy uzunluklarının aritmetik ortalamasını bulunuz.

Boy Uzunluğu (X_i)

Öğrenci Sayısı (f_i)

X_if_i

155 cm

155

160 cm

320

165 cm

1155

170 cm

2720

175 cm

3150

180 cm

1080

185 cm

740

190 cm

190

Toplam (Σ)

9510

\[ \mu = {\Sigma X_i f_i \over N} \] \[ \mu = {155 + 320 + 1155 + 2720 + 3150 + 180 + 740 + 190 \over 55} = 172.91 \approx 173 \text{ cm} \]

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu

Öğrenci Sayısı

150 – 159 cm

160 – 169 cm

170 – 179 cm

180 – 189 cm

190 – 200 cm

Toplam (Σ)

Boy uzunluklarının aritmetik ortalamasını bulunuz.

Boy Uzunluğu

m_i

Öğrenci Sayısı (f_i)

m_if_i

150 – 159 cm

155 cm

620

160 – 169 cm

165 cm

1980

170 – 179 cm

175 cm

6300

180 – 189 cm

185 cm

1480

190 – 200 cm

195 cm

390

Toplam (Σ)

10770

m_i sınıf orta sayısını belirtmektedir. (150 + 160) / 2 = 155 cm

Sınıf aralıklarında son değer aralığa dahil, başlangıç değeri dahil değildir. 160 – 170 cm aralığı gerçekte 160’dan değil 160.0000…001’den başlamaktadır. 170.000…000’da bitmektedir.

\[ \mu = {\Sigma m_i f_i \over N} \] \[ \mu = {(155 \times 4) + (165 \times 2) + (175 \times 36) + (185 \times 8) + (195 \times 2) \over 62} = 173.71 \approx 174 \text{ cm} \]

Geometrik Ortalama

Geometrik Ortalama (Geometric Mean), serinin gözlem değerlerine eşit dereceden ortalamasıdır. Aykırı değerlerden¹ daha az etkilenmesi sebebiyle aritmetik ortalamadan daha anlamlıdır. Buna rağmen seride sıfır ya da negatif değer olması durumunda kullanılamamaktadır.

Anakütle Geometrik Ortalaması

Basit Serilerde

\[ \text{Geo Ort} = \sqrt[N]{X_1X_2...X_N} \] \[ \text{Log Geo Ort} = {\Sigma logX_i \over N} \]

Frekans Serilerinde

\[ \text{Log Geo Ort} = {\Sigma f_ilogX_i \over \Sigma f_i} \]

Gruplandırılmış Serilerde

\[ \text{Log Geo Ort} = {\Sigma f_ilogm_i \over \Sigma f_i} \]

Örneklem Geometrik Ortalaması

Basit Serilerde

\[ \text{Geo Ort} = \sqrt[n]{x_1x_2...x_n} \] \[ \text{Log Geo Ort} = {\Sigma logx_i \over n} \]

Frekans Serilerinde

\[ \text{Log Geo Ort} = {\Sigma f_ilogx_i \over \Sigma f_i} \]

Gruplandırılmış Serilerde

\[ \text{Log Geo Ort} = {\Sigma f_ilogm_i \over \Sigma f_i} \]

m: Sınıf Orta Sayısı, f: Frekans

Logaritmik geometrik ortalamanın antilogaritması geometrik ortalamayı vermektedir.

Excel’de geometrik ortalama almak için
=GEOORT() formülünü kullanabiliriz.

Uygulama: 10 hastanın kan tahlili sonuçları aşağıdaki gibidir.

\[ x = 84, 244, 246, 248, 248, 250, 251, 252, 254, 1486 \]

Kan tahlili sonuçlarının geometrik ortalamasını bulunuz.

\[ \text{Log Geo Ort} = {\Sigma logx_i \over n} \] \[ \text{Log Geo Ort} = {log(84) + log(244) + log(246)\,+\,\,...\,+\,log(252) + log(254) + log(1486) \over 10} \] \[ \text{Log Geo Ort} = 2.43 \] \[ \text{AntiLog Geo Ort} = \text{Geo Ort} = 267.14 \approx 267 \]

Antilog alırken hesap makinemizde 10^{Log Geo Ort} işlemini yapabiliriz. Diğer bir ifade ile 10 üzeri (Logaritmik Geometrik Ortalama) işlemini yapmaktayız. (10^2.43 = 267.14)

Seri 84 ve 1486 olmak üzere iki aykırı değer (outlier) içermektedir. Aritmetik ortalama 356’dır ve geometrik ortalama 267 bulunmuştur. Verilerin çoğunluğu 244 ve 254 arasında dağılırken aritmetik ortalama (356) seriyi istatistiksel olarak anlamlı temsil etmemektedir. Geometrik ortalama nispeten daha anlamlıdır.

Uygulama: Anket sorularına verilen cevapların puan tablosu aşağıdaki gibidir.

Puan

Yanıt Sayısı

145

Toplam (Σ)

275

Puanların geometrik ortalamasını bulunuz.

Puan (X_i)

Yanıt Sayısı (f_i)

f_i*log(X_i)

12*log(1)

24*log(2)

30*log(3)

64*log(4)

145

145*log(5)

Toplam (Σ)

275

161.42

\[ \text{Log Geo Ort} = {\Sigma f_ilogX_i \over \Sigma f_i} = {161.42 \over 275} = 0.5870 \] \[ \text{AntiLog Geo Ort} = \text{Geo Ort} = 3.8635 \approx 3.86 \text{ puan} \]

3.86 değeri 10^0.5870 ifadesi ile denktir.

Uygulama: 67 hastanın hematoloji sonuçları aşağıdaki gibidir. (Hematoloji: Kan bilimi, NEUT: Nötrofil)

NEUT (k/uL)

Hasta Sayısı

0.00 - 1.00

1.00 - 2.00

2.00 - 3.00

3.00 - 4.00

4.00 - 5.00

5.00 - 6.00

6.00 - 7.00

Toplam (Σ)

Nötrofil sonuçlarının geometrik ortalamasını bulunuz.

NEUT (k/uL)

Sınıf Orta Sayısı (m_i)

Hasta Sayısı (f_i)

f_i*log(m_i)

0.00 - 1.00

0.50

1*log(0.50)

1.00 - 2.00

1.50

14*log(1.50)

2.00 - 3.00

2.50

22*log(2.50)

3.00 - 4.00

3.50

18*log(3.50)

4.00 - 5.00

4.50

9*log(4.50)

5.00 - 6.00

5.50

2*log(5.50)

6.00 - 7.00

6.50

1*log(6.50)

Toplam (Σ)

28.88

\[ \text{Log Geo Ort} = {\Sigma f_ilogm_i \over \Sigma f_i} = {28.88 \over 67} = 0.4311 \] \[ \text{AntiLog Geo Ort} = \text{Geo Ort} = 2.6985 \approx 2.70 \text{ k/uL} \]

Bileşik Faiz Hesaplamaları

Bileşik faiz formülünün temeli geometrik ortalamaya dayanmaktadır.

Yıl

Anapara

Faiz Oranı

Faiz Geliri

1000

%10

100

1100

%20

220

1320

%15

198

3. yılın sonunda Anapara + Faiz Geliri = 1320 + 198 = 1518 TL’dir. Sonuç olarak yatırımcı 1000 TL ile açtığı mevduat hesabından vade sonunda %51.8 getiri elde etmiştir.

\[ \text{Geo Ort} = \sqrt[n]{X_1X_2...X_n} \]

Geometrik ortalamayı yukarıdaki gibi ifade etmiştik. Formül aynı zamanda

\[ \text{Geo Ort} = (X_1X_2...X_n)^{1 \over n} \]

gösterimi ile aynıdır.

\[ \text{Bilesik Faiz} = [(1 + r_1)(1 + r_2)...(1 + r_n)]^{1 \over n} - 1 \]

r: faiz oranı, n: dönem sayısı

Dikkat edilirse geometrik ortalama ve bileşik faiz formülü birbirine çok benzemektedir. Bu sebeple bileşik faize aynı zamanda faiz oranlarının geometrik ortalaması diyebiliriz.

\[ \text{Bilesik Faiz} = [(1 + 0.10)(1 + 0.20)(1 + 0.15)]^{1 \over 3} - 1 = 1.518^{1 \over 3} - 1 \approx 0.1493 \approx \%14.93 \]

Parantez içindeki çarpımların sonucu 1.518’dir. Anapara + faiz gelirini ise 1518 TL hesaplamıştık. Çarpımdan 1 çıkartırsak (1.518 – 1) toplam faiz gelirin yüzdesini buluruz. (%51.8) Bulduğumuz %14.93 bileşik faiz oranının sağlamasını yapmak istersek

\[ \text{Bilesik Faiz} = [(1 + 0.1493)(1 + 0.1493)(1 + 0.1493)]^{1 \over 3} - 1 = 1.518^{1 \over 3} - 1 \approx 0.1493 \approx \%14.93 \]

aynı sonuca ulaşırız.

Yorumlanması şu şekildedir:

Yatırımcı 1000 TL anaparasını 3 yıl boyunca sırasıyla %10, %15 ve %20 faiz oranlarından bileşik faize yatırmak yerine %14.93 sabit oranı ile bileşik faize yatırırsa vade sonunda aynı getiriyi elde edecektir. (%51.8)

Harmonik Ortalama

Harmonik Ortalama (Harmonic Mean), değişkenlerden birinin sabit, diğerinin sabit olmadığı durumlarda kullanılan, genellikle hız, fiyat ve verimlilik hesaplamalarında tercih edilen ortalama türüdür. Aykırı değerlerden en az etkilenen duyarlı ortalamadır. Hesaplanabilmesi için seride sıfır ve negatif değer olmamalıdır.

Anakütle Harmonik Ortalaması

Basit Serilerde

\[ \text{Hrm Ort} = {N \over \Sigma {1 \over X_i}} \]

Frekans Serilerinde

\[ \text{Hrm Ort} = {\Sigma f_i \over \Sigma {f_i \over X_i}} \]

Gruplandırılmış Serilerde

\[ \text{Hrm Ort} = {\Sigma f_i \over \Sigma {f_i \over m_i}} \]

Örneklem Harmonik Ortalaması

Basit Serilerde

\[ \text{Hrm Ort} = {n \over \Sigma {1 \over x_i}} \]

Frekans Serilerinde

\[ \text{Hrm Ort} = {\Sigma f_i \over \Sigma {f_i \over x_i}} \]

Gruplandırılmış Serilerde

\[ \text{Hrm Ort} = {\Sigma f_i \over \Sigma {f_i \over m_i}} \]

m: Sınıf Orta Sayısı, f: Frekans

Excel’de harmonik ortalama almak için
=HARORT() formülünü kullanabiliriz.

Uygulama: Bir araç A noktasından B noktasına sırasıyla 40, 60 ve 80 km/saat hızla gitmektedir. Aracın ortalama hızını bulunuz.

\[ \text{Hrm Ort} = {n \over \Sigma {1 \over x_i}} = {3 \over {1 \over 40} + {1 \over 60} + {1 \over 80}} = 55.38 \text{ km/saat} \]

Diyelim ki A ve B noktası arasındaki mesafe 240 km olsun. Araç A ve B noktasına toplamda 3 kere gitmekte ve 240 * 3 = 720 km yol yapmaktadır. Toplam mesafeyi 720/55.38 = 13 saatte tamamlamaktadır.

Yolda geçen süreyi tek tek hesapladığımızda 240/40 = 6 saat, 240/60 = 4 saat, 240/80 = 3 saat

6 + 4 + 3 = 13 saat sonucuna varırız. Bu şekilde harmonik ortalamanın sağlamasını yapabiliriz.

Yorumlaması ise şu şekildedir:

Araç aynı yolu 40, 60 ve 80 km/saat hızlarla gitmek yerine 55.38 km/saat gibi sabit bir hızla giderse aynı sürede tamamlar.

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu

Öğrenci Sayısı

155 cm

160 cm

165 cm

170 cm

175 cm

180 cm

185 cm

190 cm

Toplam (Σ)

Boy uzunluklarının harmonik ortalamasını bulunuz.

Boy Uzunluğu (X_i)

Öğrenci Sayısı (f_i)

f_i/X_i

155 cm

1/155

160 cm

2/160

165 cm

7/165

170 cm

16/170

175 cm

18/175

180 cm

6/180

185 cm

4/185

190 cm

1/190

Toplam (Σ)

0.32

\[ \text{Hrm Ort} = {\Sigma f_i \over \Sigma {f_i \over X_i}} = { 55 \over 0.32} = 172.65 \approx 173 \text{ cm} \]

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu

Öğrenci Sayısı

150 – 159 cm

160 – 169 cm

170 – 179 cm

180 – 189 cm

190 – 200 cm

Toplam (Σ)

Boy uzunluklarının harmonik ortalamasını bulunuz.

Boy Uzunluğu

m_i

Öğrenci Sayısı (f_i)

f_i/m_i

150 – 159 cm

155 cm

4/155

160 – 169 cm

165 cm

12/165

170 – 179 cm

175 cm

36/165

180 – 189 cm

185 cm

8/185

190 – 200 cm

195 cm

2/195

Toplam (Σ)

0.36

\[ \text{Hrm Ort} = {\Sigma f_i \over \Sigma {f_i \over m_i}} = {62 \over 0.36} = 173.31 \approx 173 \text{ cm} \]

Kareli Ortalama

Kareli Ortalama (Root Mean Square, RMS, Quadratic Mean), aritmetik ortalamaya benzemekle birlikte serideki 0 ve negatif değerleri nötralize etmek için kullanılan ortalama türüdür. Diğer bir ifade ile seride 0 veya negatif değerler göz ardı edilmek isteniyorsa kareli ortalama kullanılmalıdır.

Anakütle Kareli Ortalaması

Basit Serilerde

\[ \text{Kareli Ort} = \sqrt { {\Sigma {X_i}^2} \over N } \]

Frekans Serilerinde

\[ \text{Kareli Ort} = \sqrt { {\Sigma f_i{X_i}^2} \over \Sigma f_i } \]

Gruplandırılmış Serilerde

\[ \text{Kareli Ort} = \sqrt { {\Sigma f_i{m_i}^2} \over \Sigma f_i } \]

Örneklem Kareli Ortalaması

Basit Serilerde

\[ \text{Kareli Ort} = \sqrt { {\Sigma {x_i}^2} \over n } \]

Frekans Serilerinde

\[ \text{Kareli Ort} = \sqrt { {\Sigma f_i{x_i}^2} \over \Sigma f_i } \]

Gruplandırılmış Serilerde

\[ \text{Kareli Ort} = \sqrt { {\Sigma f_i{m_i}^2} \over \Sigma f_i } \]

m: Sınıf Orta Sayısı, f: Frekans

Excel’de kareli ortalamanın formülü bulunmamaktadır.
=KAREKÖK(TOPKARE()/BAĞ_DEĞ_SAY()) formül kombinasyonu kullanılabilir.

Uygulama: Yedi günlük hava sıcaklığı değerleri aşağıda verilmiştir.

\[ x = -4, -2, 0, 4, 8, 13, 13 \text{ } ^{\circ}C \]

Sıcaklık değerlerinin kareli ortalamasını bulunuz.

\[ \text{Kareli Ort} = \sqrt { {\Sigma {x_i}^2} \over n } = \sqrt { { {-4}^2 + {-2}^2 \,+\,\,...\,+\, 13^2 + 13^2 } \over 7 } = \sqrt { 438 \over 7 } = 7.91 \approx 8^{\circ}C \]

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu

Öğrenci Sayısı

155 cm

160 cm

165 cm

170 cm

175 cm

180 cm

185 cm

190 cm

Toplam (Σ)

Boy uzunluklarının kareli ortalamasını bulunuz.

Boy Uzunluğu (X_i)

Öğrenci Sayısı (f_i)

f_i*X_i²

155 cm

1*155²

160 cm

2*160²

165 cm

7*165²

170 cm

16*170²

175 cm

18*175²

180 cm

6*180²

185 cm

4*185²

190 cm

1*190²

Toplam (Σ)

1,646,850

\[ \text{Kareli Ort} = \sqrt { {\Sigma f_i{X_i}^2} \over \Sigma f_i } = \sqrt { 1646850 \over 55} = 173.04 \approx 173 \text{ cm} \]

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu

Öğrenci Sayısı

150 – 159 cm

160 – 169 cm

170 – 179 cm

180 – 189 cm

190 – 200 cm

Toplam (Σ)

Boy uzunluklarının kareli ortalamasını bulunuz.

Boy Uzunluğu

m_i

Öğrenci Sayısı (f_i)

f_i*m_i²

150 – 159 cm

155 cm

4*155²

160 – 169 cm

165 cm

12*165²

170 – 179 cm

175 cm

36*165²

180 – 189 cm

185 cm

8*185²

190 – 200 cm

195 cm

2*195²

Toplam (Σ)

1,875,150

\[ \text{Kareli Ort} = \sqrt { {\Sigma f_i{m_i}^2} \over \Sigma f_i } = \sqrt { 1875150 \over 62} = 173.91 \approx 174 \text{ cm} \]

Ağırlıklı Ortalama

Ağırlıklı Ortalama (Weighted Mean) ya da Tartılı Aritmetik Ortalama finans alanında sıkça kullanılan duyarlı ortalamalardan biridir. Aralarındaki ilişkiden dolayı değişkenlerden biri ya da birkaçı ağırlıklandırılır, hesaplanmak istenen asıl değişkenin ortalaması bulunur. Özel durumlarda kullanılır ve diğer ortalama türlerine göre istatistiksel olarak daha anlamlıdır.

Anakütle Ağırlıklı Ortalaması

Basit Serilerde

\[ \text{Agırlıklı Ort} = { {\Sigma w_iX_i} \over \Sigma X_i } \]

Örneklem Ağırlıklı Ortalaması

Basit Serilerde

\[ \text{Agırlıklı Ort} = { {\Sigma w_ix_i} \over \Sigma x_i } \]

Excel’de ağırlıklı ortalamanın formülü bulunmamaktadır.
=TOPLA.ÇARPIM()/TOPLA() formül kombinasyonu kullanılabilir.

Uygulama: Aşağıda beş farklı mevduat hesabının tutarları ve faiz oranları verilmiştir.

Hesap Numarası

Tutar

Faiz Oranı

A000001

2,000,000

10.20

A000002

5,000,000

10.40

A000003

1,000,000

10.10

A000004

4,000,000

10.30

A000005

120,000,000

11.10

Toplam (Σ)

132,000,000 TL

Faiz oranlarının ağırlıklı ortalamasını bulunuz.

Hesap Numarası

Tutar (x_i)

Faiz Oranı (w_i)

Faiz Oranı * Tutar

A000001

2,000,000

10.20

10.20*(2,000,000)

A000002

5,000,000

10.40

10.40*(5,000,000)

A000003

1,000,000

10.10

10.10*(1,000,000)

A000004

4,000,000

10.30

10.30*(4,000,000)

A000005

120,000,000

11.10

11.10*(120,000,000)

Toplam (Σ)

132,000,000 TL

1,455,700,000 TL

\[ \text{Agırlıklı Ort} = { {\Sigma w_ix_i} \over \Sigma x_i } = { 1,455,700,000 \over 132,000,000 } = 11.03 \]

Faiz oranlarının aritmetik ortalaması 10.42’dir ve istatistiksel olarak anlamlı değildir. İşlem tutarlarının büyük çoğunluğu (%91’lik kısmı oluşturan 132 milyon TL’lik hesap) 11.10 faiz oranı ile fiyatlanmıştır. Ortalamanın 11.10’a yakın olması beklenir. Bu sebeple 11.03 ağırlıklı ortalama faiz oranı, 10.42 aritmetik ortalamasına göre istatistiksel olarak daha anlamlıdır.

Duyarlı Ortalamaların Karşılaştırılması

Uygulamada çoğunlukla aritmetik ortalama kullanılsa da aykırı değerlerin yüksek olduğu serilerde geometrik ve harmonik ortalama tercih edilebilir. Geometrik ve harmonik ortalama hesaplamalarında seride negatif ve sıfır değerlerinin bulunmamasına dikkat edilmelidir. Ağırlıklı ortalama ise stok faiz oranı gibi özel durumlarda tercih edilen, basit serilerde kullanılamayan özel bir duyarlı ortalamadır.

\[ \text{Kareli Ort} \geq \text{Aritmetik Ort} \geq \text{Geometrik Ort} \geq \text{Harmonik Ort} \]

Tüm serilerde yukarıdaki büyüklük sıralaması geçerlidir. Harmonik ortalama aykırı değerlerden en az etkilenen duyarlı ortalama olmakla birlikte aykırı değerlerin yoğun olduğu serilerde kareli ortalama güvenirliği en az olan ortalama türüdür.

X₁ = 10, 10, 11, 11, 12, 12, 480 basit serisinin duyarlı ortalamaları hesaplandığında sırasıyla

\[ \text{Kareli Ort} \geq \text{Aritmetik Ort} \geq \text{Geometrik Ort} \geq \text{Harmonik Ort} \] \[ 182 \geq 78 \geq 19 \geq 13 \]

ortalamaları bulunur. 480 aykırı değeri seriden çıkarıldığında serinin aritmetik ortalaması 11 olmaktadır. Bu sebeple aykırı değerin varlığı durumunda harmonik ortalama (13) seri ortalamasını istatistiksel olarak daha anlamlı ifade ettiği sonucuna varılabilir.

Seri karşılaştırmalarında harmonik ortalama istatistiksel olarak daha anlamlı iken aykırı değerlerin varlığı kabul edildiği durumlarda aritmetik ortalamanın kullanılmasında sakınca bulunmamaktadır. Bununla birlikte aykırı değerlerin yoğun olduğu serilerde medyan gibi duyarlı olmayan ortalamalar tercih edilmektedir. Günümüzde gini katsayısının yüksek olduğu ülkelerde medyan değerleri, kişi başına milli gelir karşılaştırmalarında aritmetik ortalamaya göre daha gerçekçi sonuçlar vermektedir.²

SPSS'te Duyarlı Ortalamalar

Aritmetik Ortalama

Sadece aritmetik ortalama bulunmak isteniyorsa aşağıdaki adımlar uygulanır.³

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

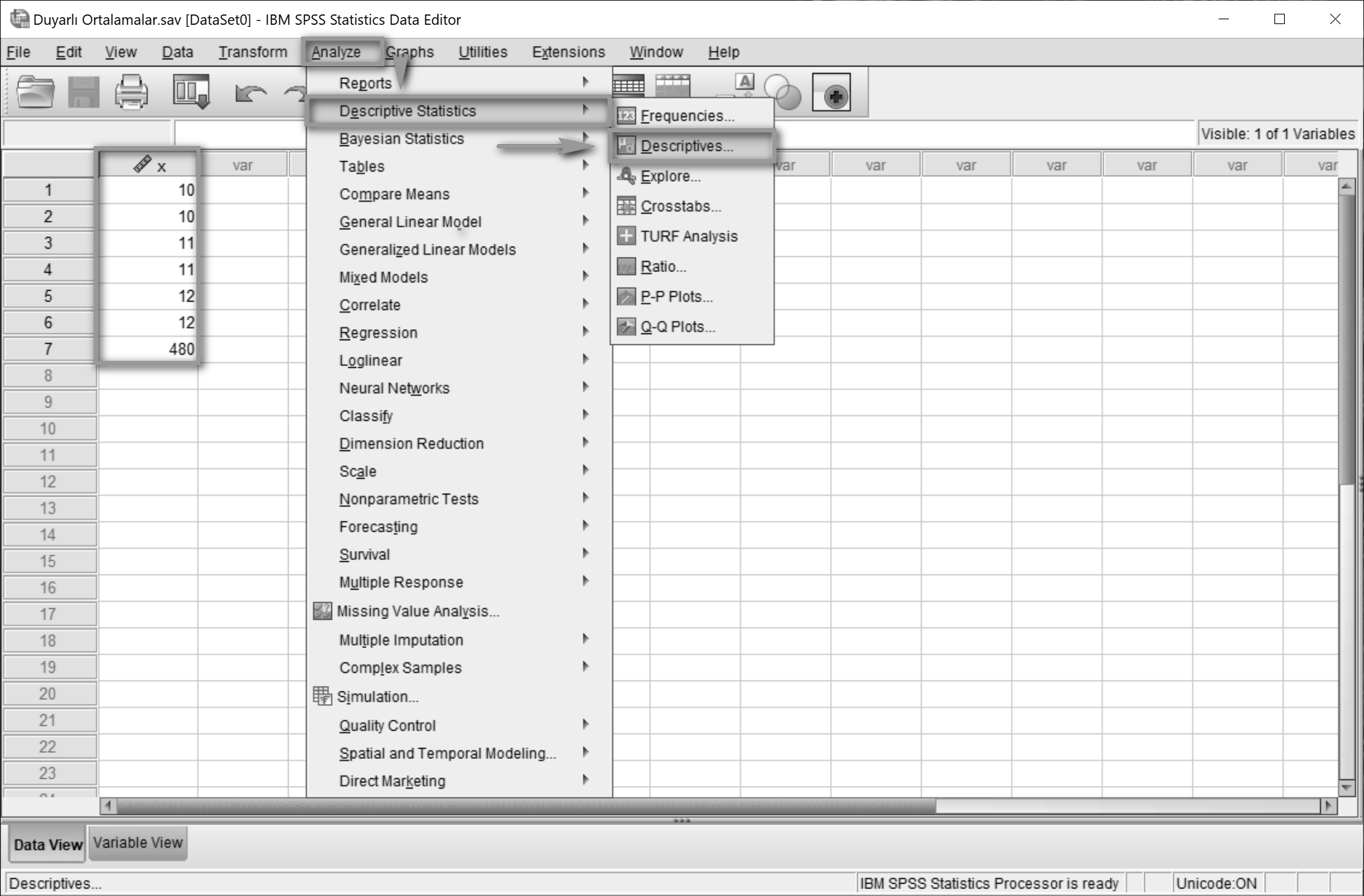
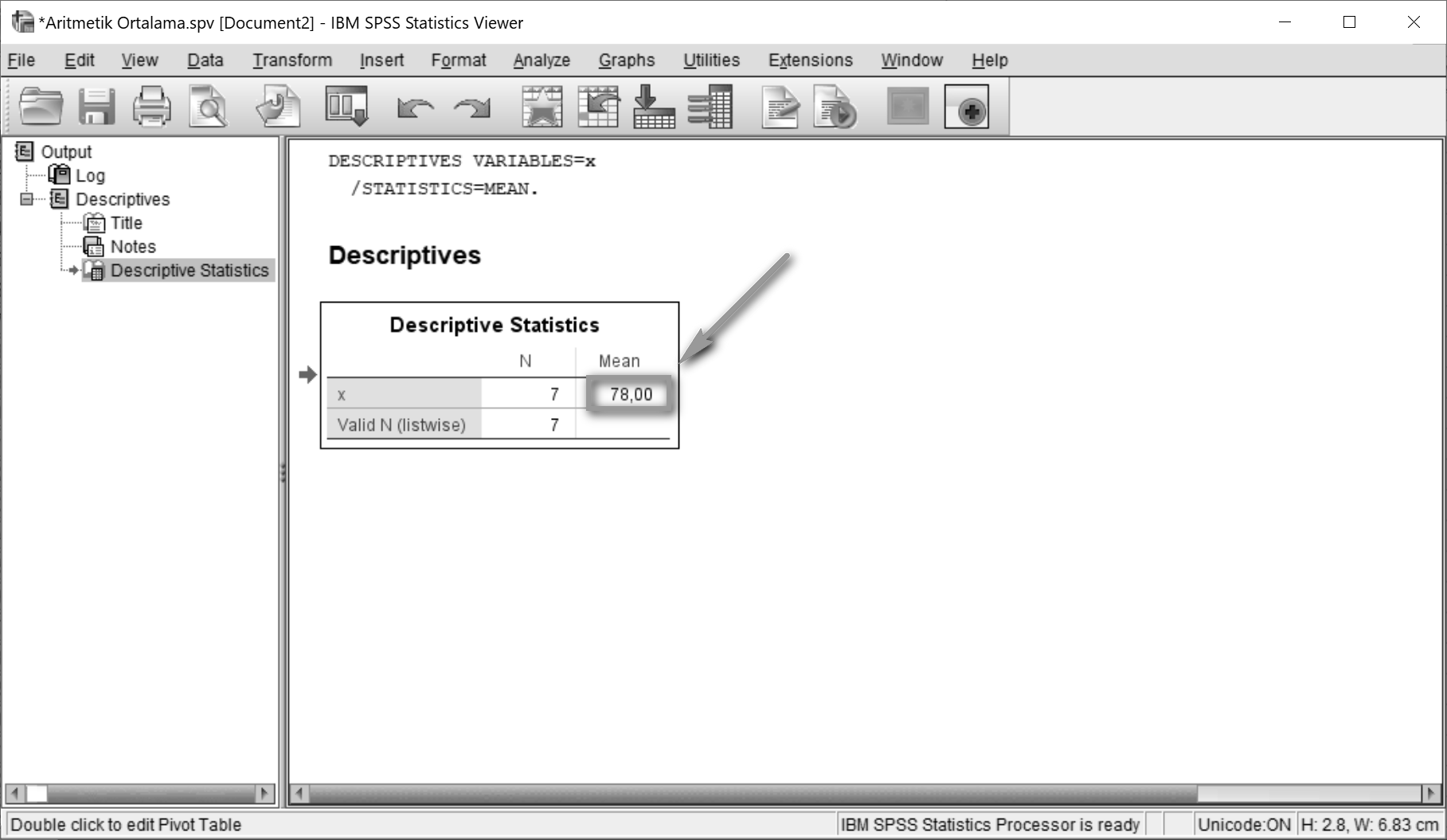
Analyze > Descriptive Statistics > Descriptives… yolu izlenir.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

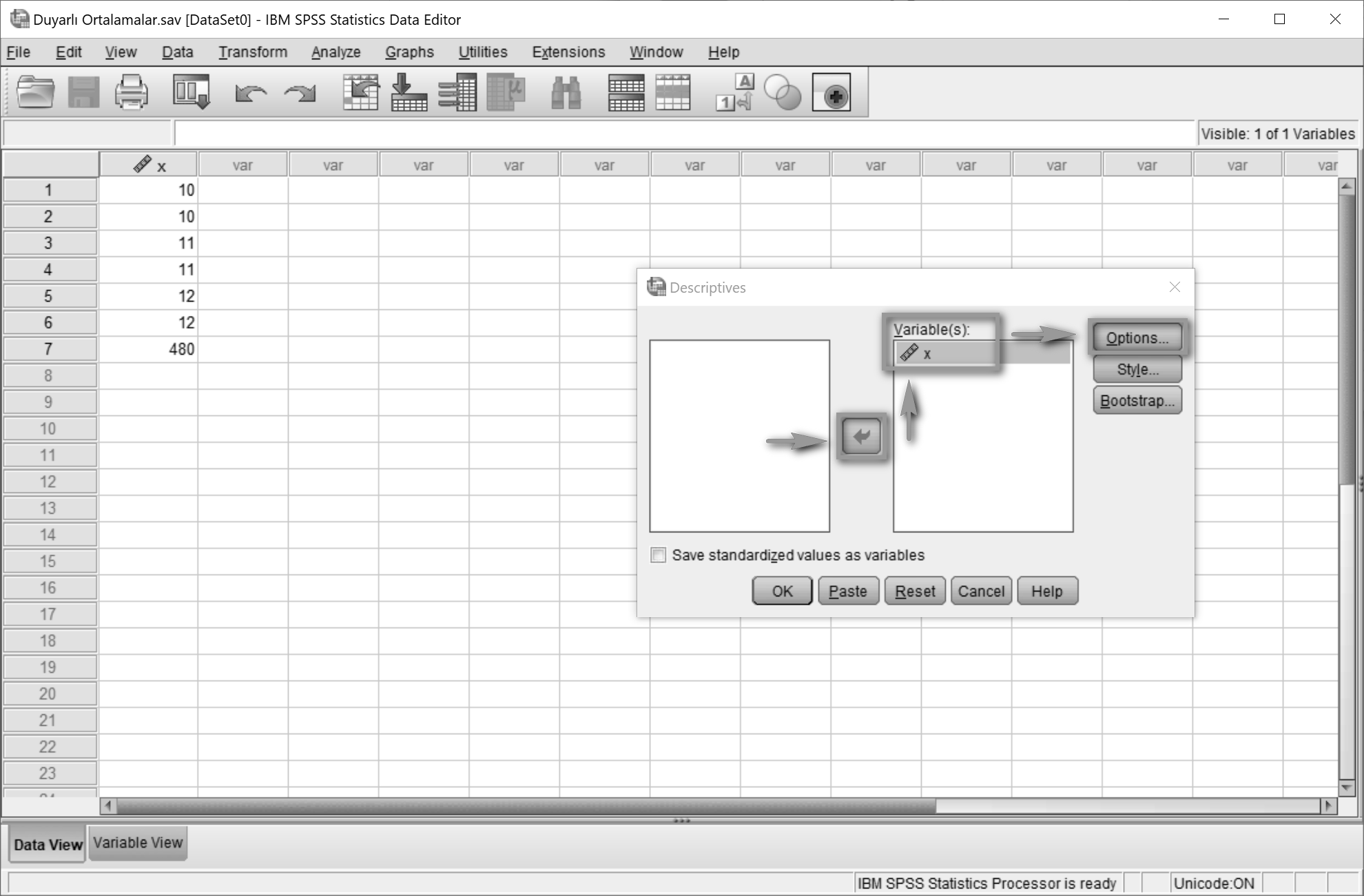
İlgili değişken Variable(s)⁴ alanına taşınır. Options⁵’a tıklanır.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

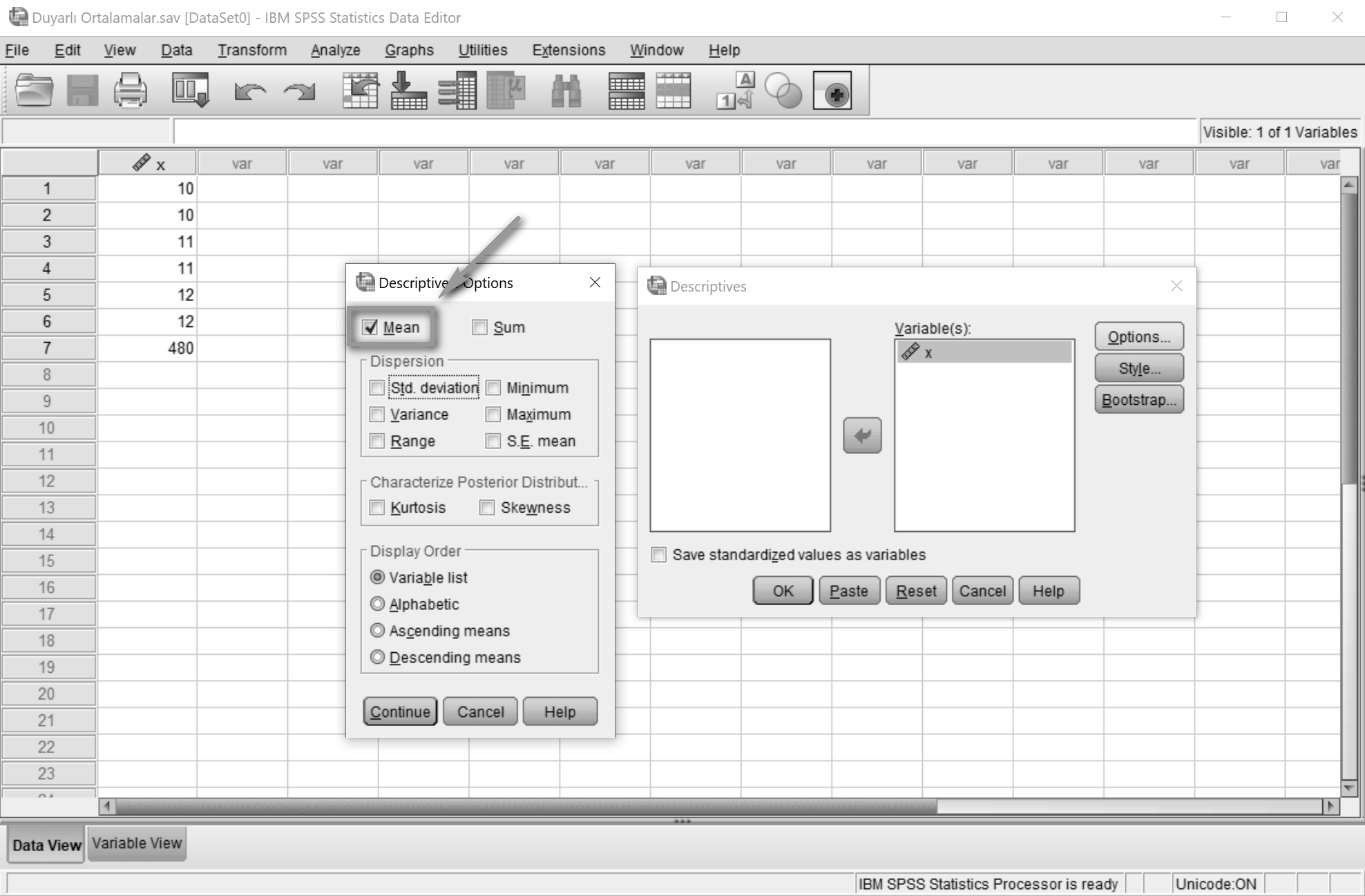
Açılan pencerede sadece Mean⁶ seçilir.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

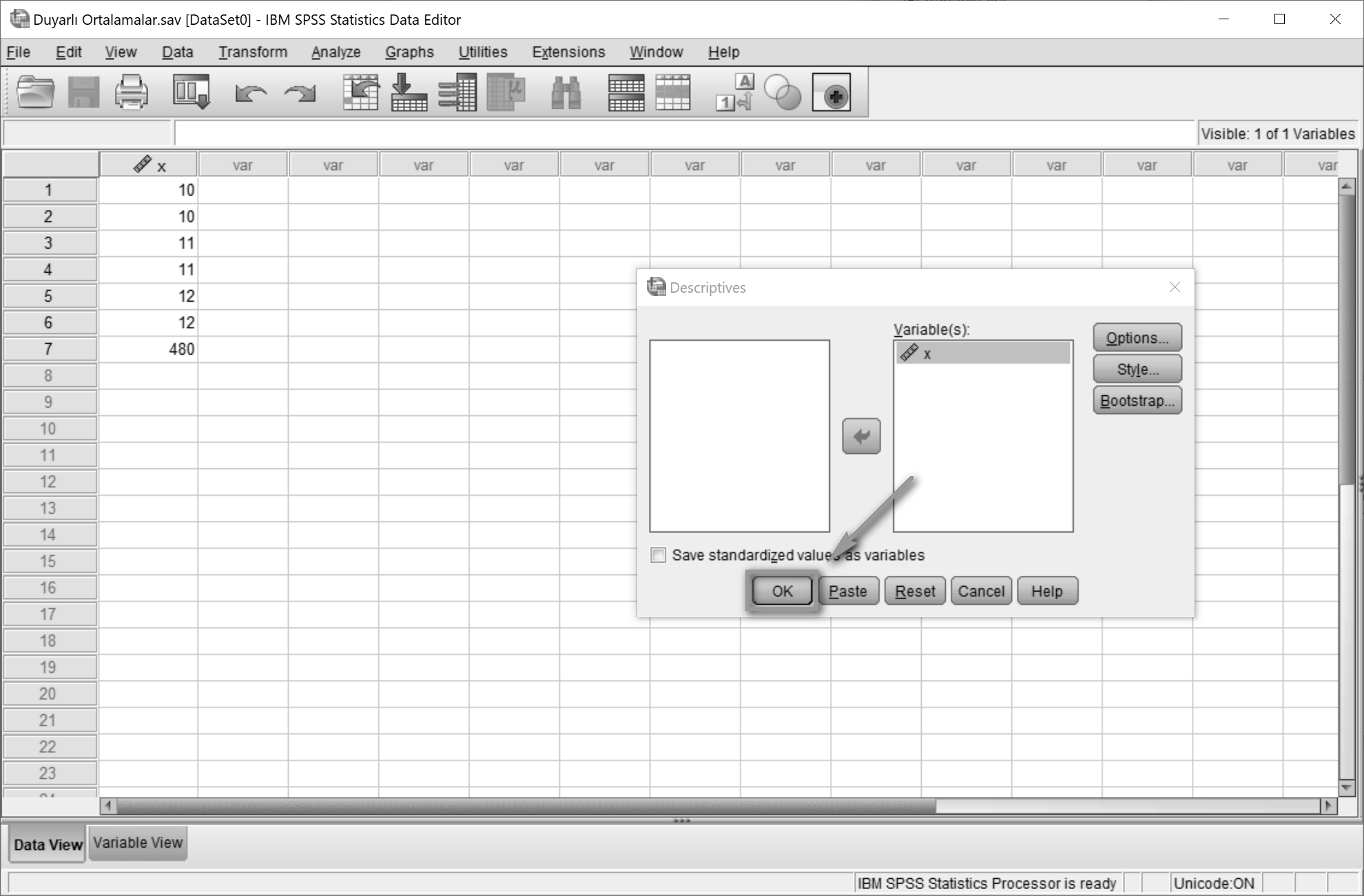
OK'a tıklanır.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

x₁ = 10, 10, 11, 11, 12, 12, 480 serisine ait aritmetik ortalamanın 78 olduğu bulunur.

Aritmetik, Geometrik ve Harmonik Ortalama

Aritmetik, geometrik ve harmonik ortalama birlikte bulunmak isteniyorsa aşağıdaki adımlar uygulanır.

spss aritmetik geometrik harmonik ortalama

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

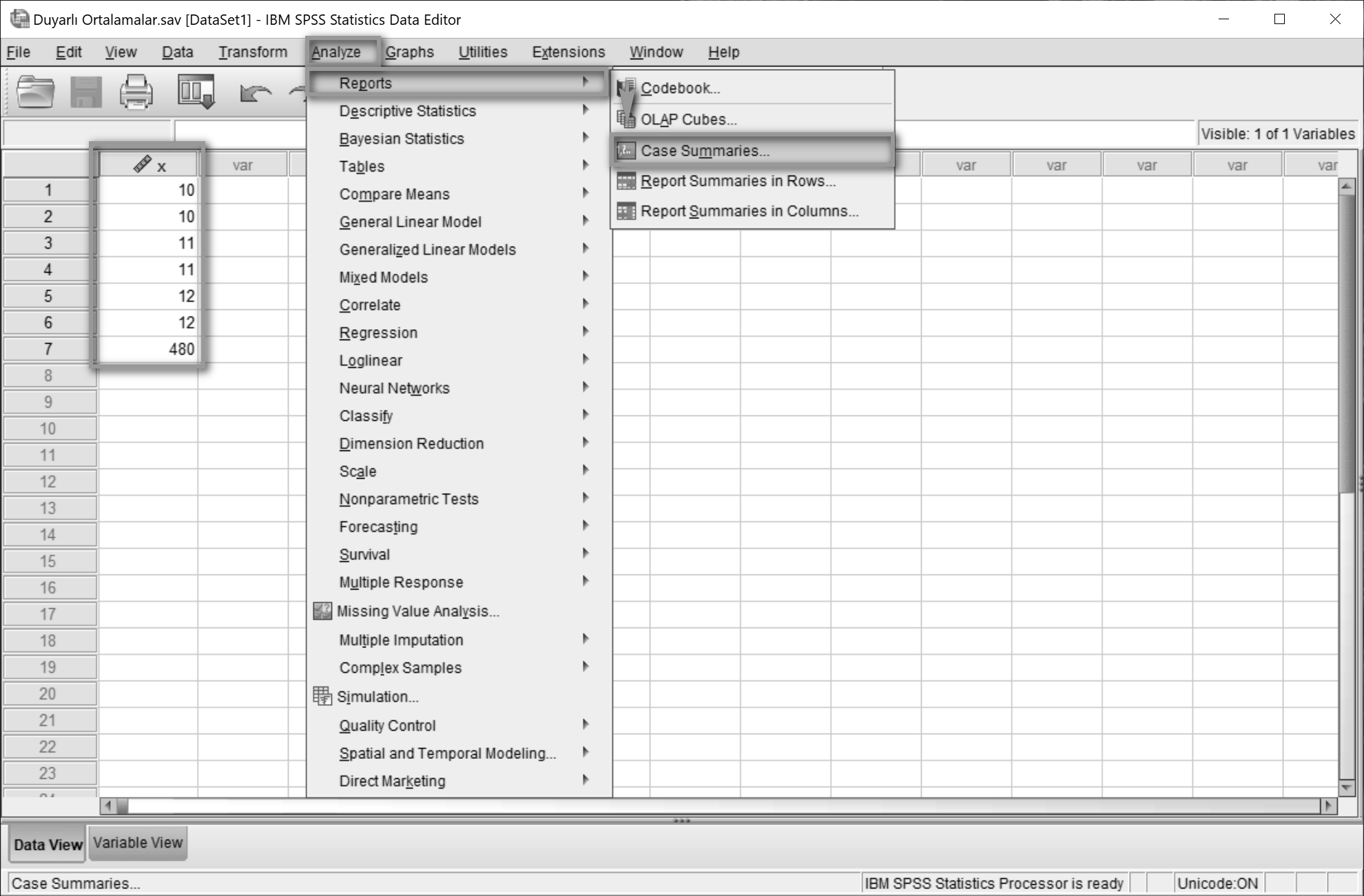
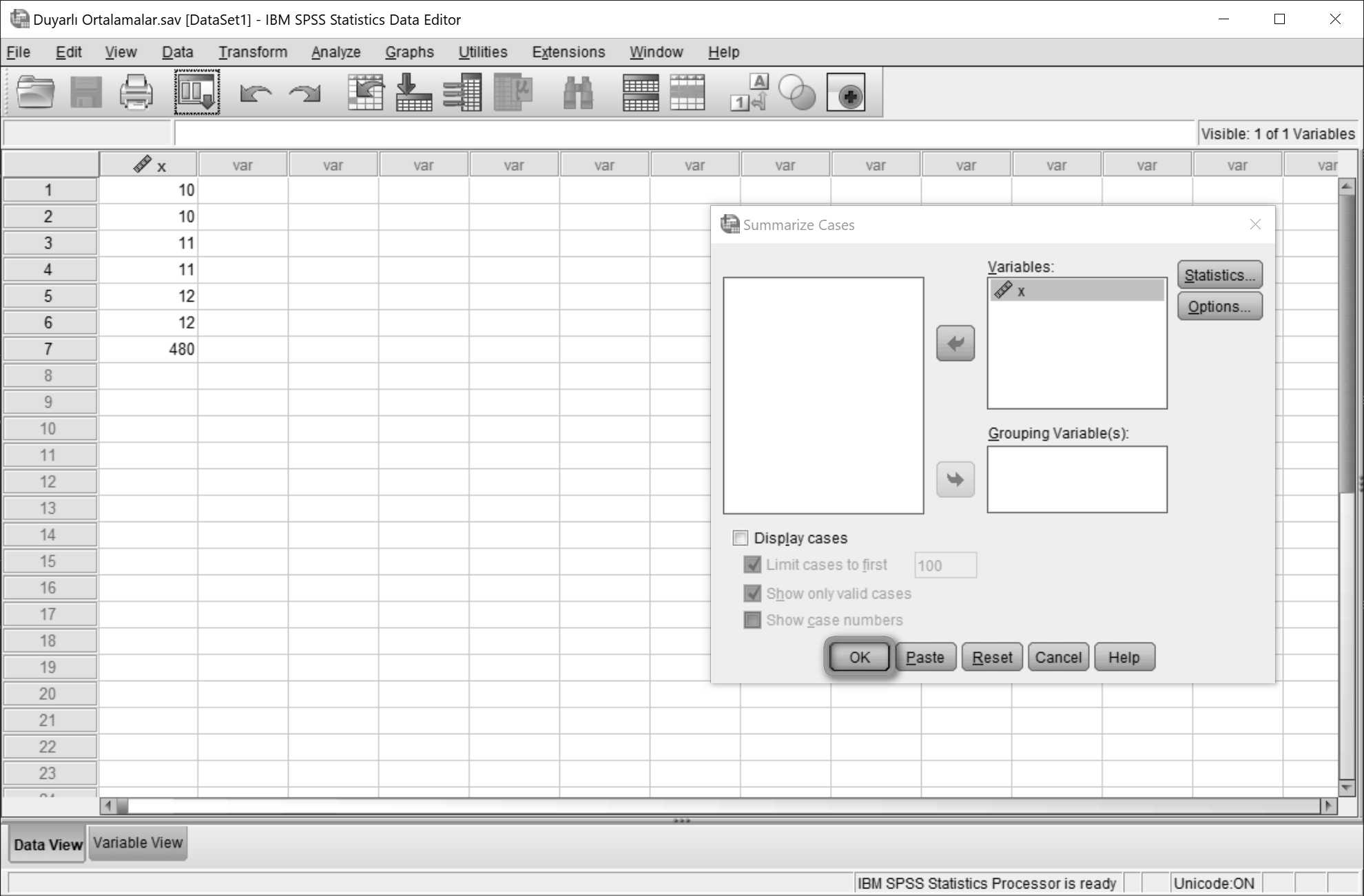
Analyze > Reports > Case Summaries… yolu izlenir.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

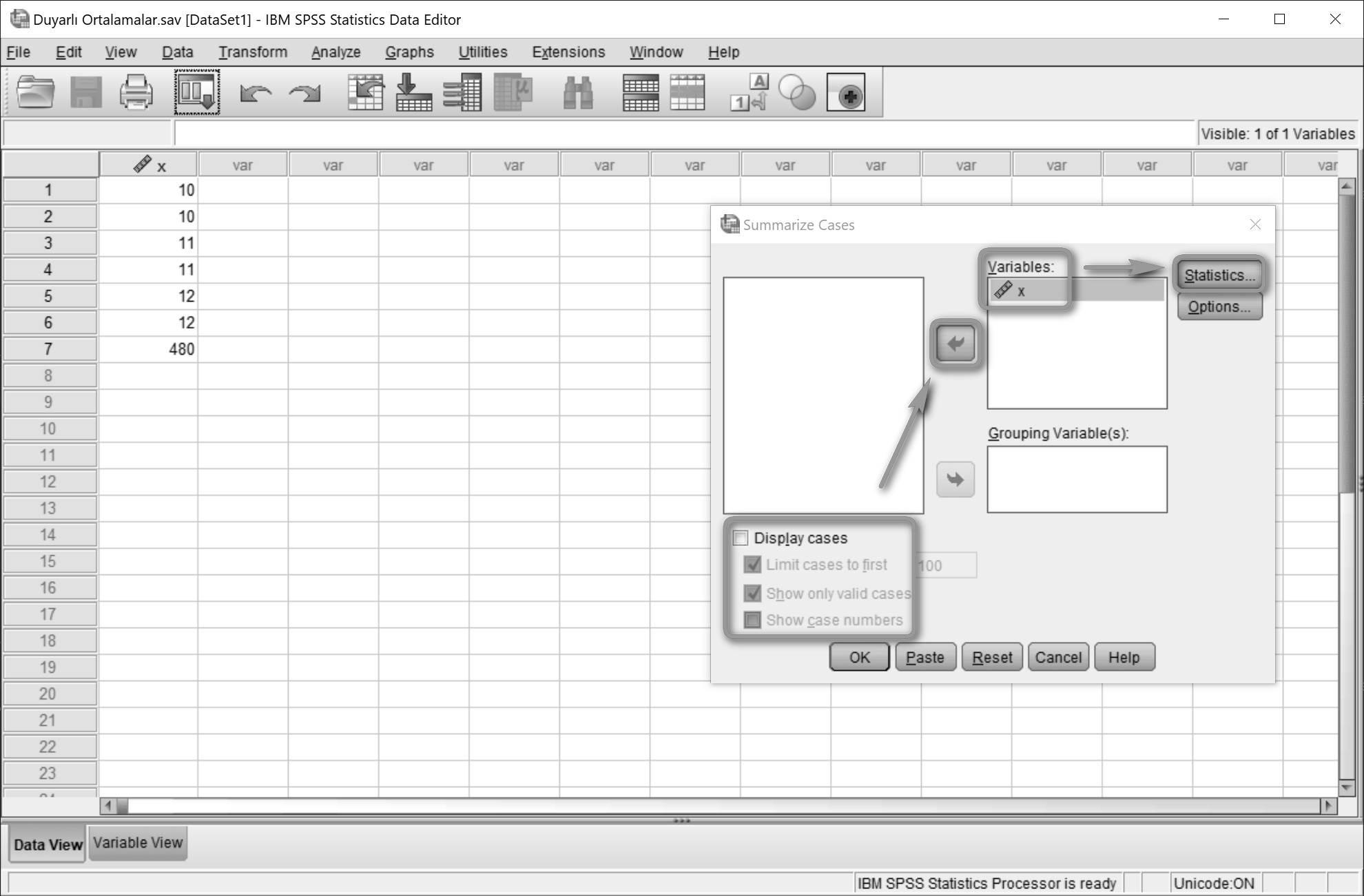
Display cases seçimi kaldırılır. (Kaldırılmadığı takdirde tüm seri değerleri rapora eklenecektir.)

Statistics…’e tıklanır.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

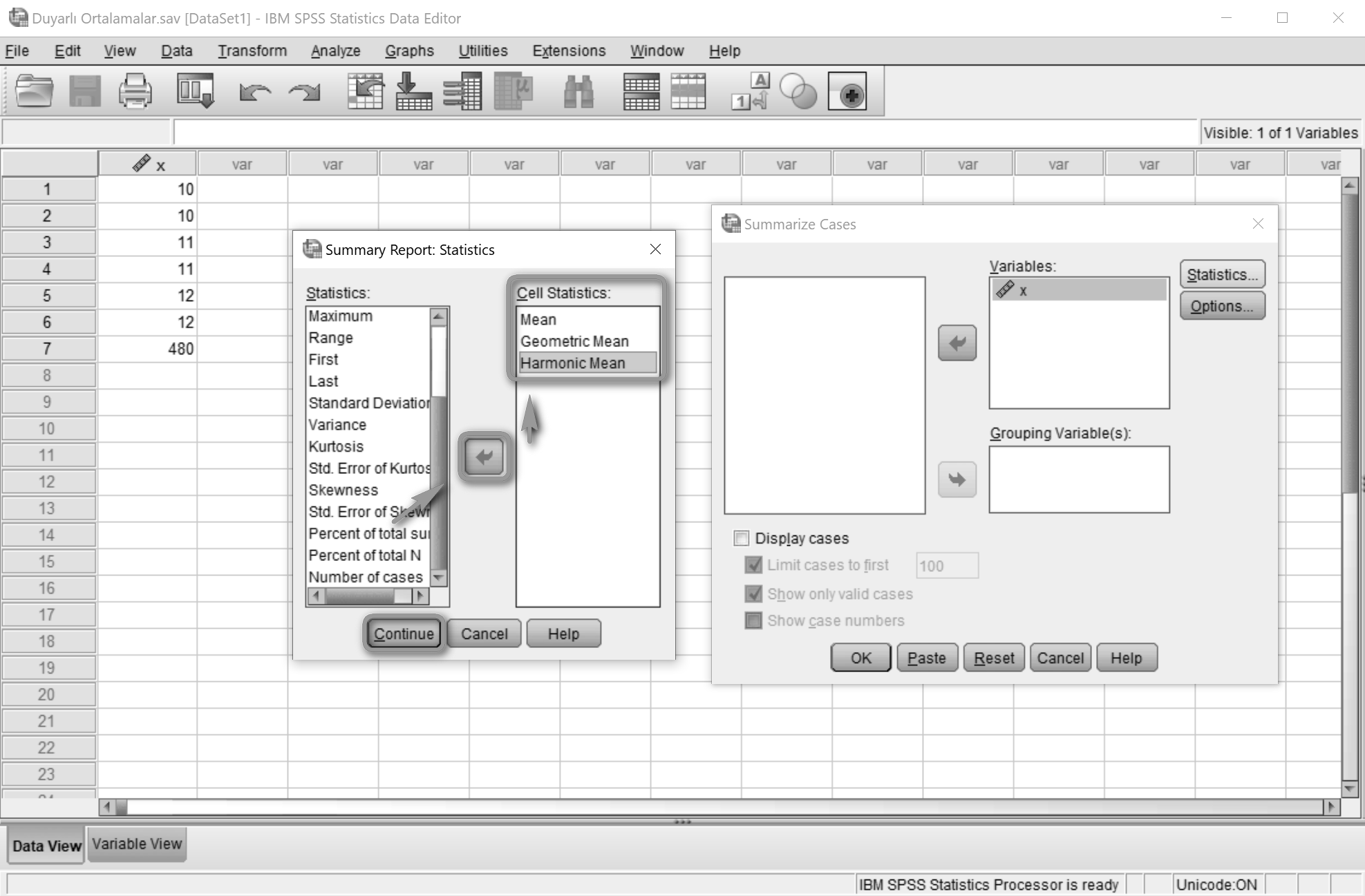
Statistics listesinden Mean, Geometric Mean ve Harmonic Mean seçilir. Cell Statistics alanına aktarılır.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

Summarize Cases penceresinde OK'a tıklanır.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

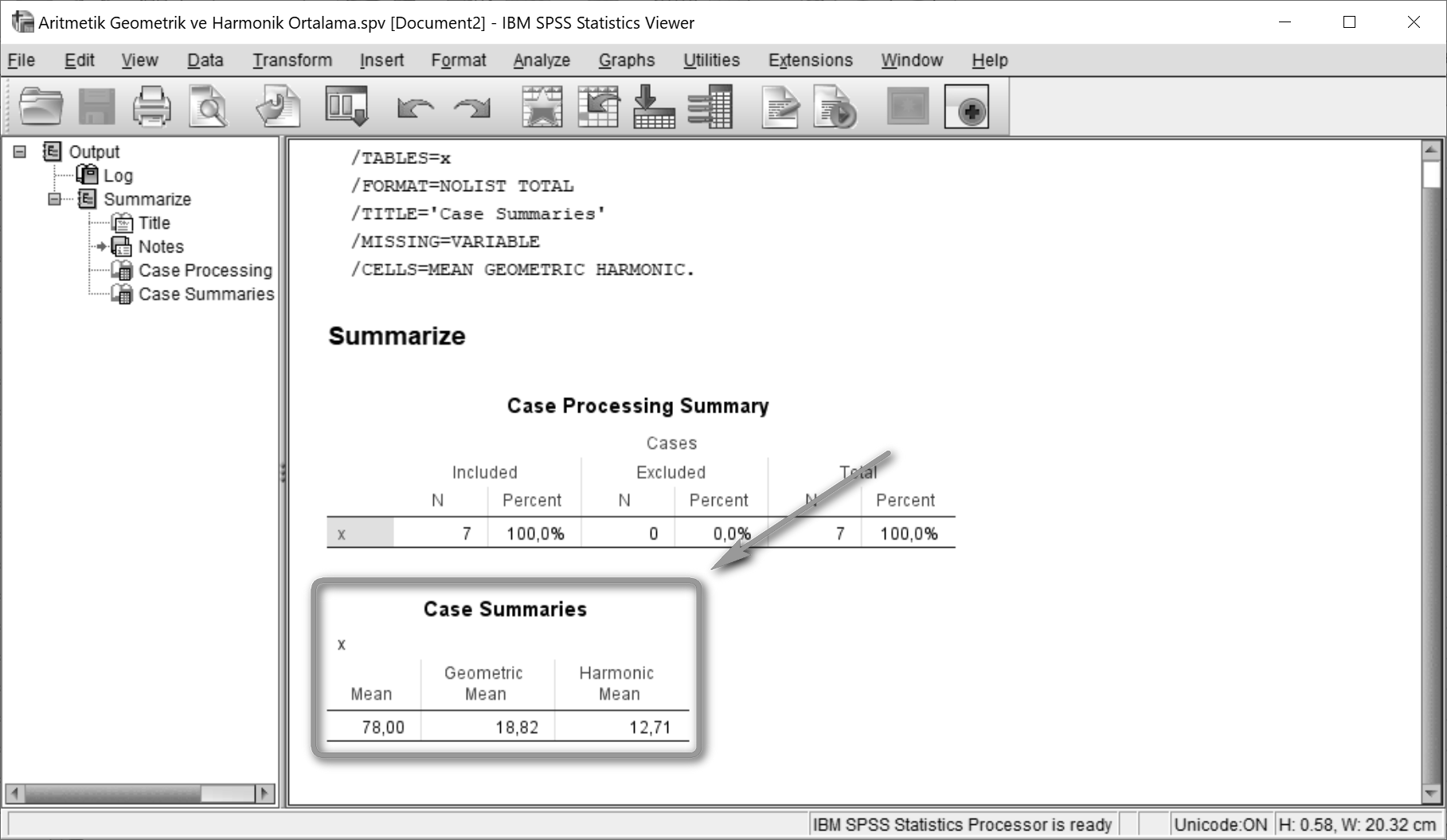
Aritmetik, geometrik ve harmonik ortalamalar görseldeki gibi bulunur.

Aritmetik ortalama ve harmonik ortalama arasındaki fark ne kadar büyükse seride aykırı değerlerin varlığından söz edilebilir. Aykırı değerleri tespit edebilmek için Summarize Cases penceresinde “Display cases” kutusu seçilmelidir.

Medyan

Medyan (Median) ya da Ortanca küçükten büyüğe sıralanmış veri dizisinin ortasındaki değeri ifade eden duyarlı olmayan ortalamadır. Aykırı değerlerin olduğu serilerde diğer ortalama türlerine göre daha güvenilirdir.

x̃ işareti (x üzeri tilde) medyanın istatistikteki sembolüdür.

Anakütle Medyan Değeri

Gözlem Sayısının Tek Olduğu Basit Serilerde

\[ \tilde X = {X_{N+1 \over 2}} \]

Gözlem Sayısının Çift Olduğu Basit Serilerde

\[ \tilde X = { { X_{N\over 2} } + { X_{ { N\over 2}+1 } } \over 2} \]

Frekans Toplamının Tek Sayı Olduğu Frekans Serilerinde

\[ \tilde X = { X_{ {(\Sigma f_i) + 1 } \over 2 } } \]

Frekans Toplamının Çift Sayı Olduğu Frekans Serilerinde

\[ \tilde X = { { X_{ \Sigma f_i \over 2 } + X_{ { \Sigma f_i \over 2 } + 1 } } \over 2 } \]

Gruplandırılmış Serilerde

\[ \tilde X = \text{Low}_\text{med} + { { { \Sigma f_i \over 2 } - { \text{f}_\text{medPre} } }\over \text{f}_\text{med} } * \text{ClassInt} \]

Low_med: Medyan sınıfının alt değeri. (Medyan sınıfı bulunurken toplam frekans (Σfi) 2’ye bölünür.)
f_medPre: Medyan sınıfından bir önceki sınıfa kadar olan frekanslar toplamı
f_med: Medyan sınıfının frekansı
ClassInt (Class Interval): Sınıf aralığı

Örneklem Medyan Değeri

Gözlem Sayısının Tek Olduğu Basit Serilerde

\[ \tilde x = {x_{n+1 \over 2}} \]

Gözlem Sayısının Çift Olduğu Basit Serilerde

\[ \tilde x = { { x_{n\over 2} } + { x_{ { n\over 2}+1 } } \over 2} \]

Frekans Toplamının Tek Sayı Olduğu Frekans Serilerinde

\[ \tilde x = { x_{ {(\Sigma f_i) + 1 } \over 2 } } \]

Frekans Toplamının Çift Sayı Olduğu Frekans Serilerinde

\[ \tilde x = { { x_{ \Sigma f_i \over 2 } + x_{ { \Sigma f_i \over 2 } + 1 } } \over 2 } \]

Gruplandırılmış Serilerde

\[ \tilde x = \text{Low}_\text{med} + { { { \Sigma f_i \over 2 } - { \text{f}_\text{medPre} } }\over \text{f}_\text{med} } * \text{ClassInt} \]

Low_med: Medyan sınıfının alt değeri. (Medyan sınıfı bulunurken toplam frekans (Σfi) 2’ye bölünür.)
f_medPre: Medyan sınıfından bir önceki sınıfa kadar olan frekanslar toplamı
f_med: Medyan sınıfının frekansı
ClassInt (Class Interval): Sınıf aralığı

f: Frekans, N ve n Gözlem Sayısı

Excel’de medyan değerini bulmak için
=ORTANCA() formülünü kullanabiliriz.

Uygulama: X = 24, 12, 17, 13, 8, 8, 8, 8, 46 serisinin medyan değerini bulunuz.

Medyan değeri hesaplanırken öncelikle seri küçükten büyüğe sıralanır.

X = 8, 8, 8, 8, 12, 13, 17, 24, 46

N: 9’dur. (9 adet gözlem sayısı vardır.) Gözlem sayısı tek sayı olduğu için

\[ \tilde X = {X_{N+1 \over 2}} = {X_{9+1 \over 2}} = {X_5} = 12 \]

X₅, serinin 5. değeri 12 medyan değeridir.

Uygulama: x = 48, 50, 50, 52, 54, 54, 54, 56 serisinin medyan değerini bulunuz.

n: 8’dir. Gözlem sayısı çift sayı olduğu için

\[ \tilde x = { { x_{n\over 2} } + { x_{ { n\over 2}+1 } } \over 2 } = { { x_{8\over 2} } + { x_{ { 8\over 2}+1 } } \over 2 } = { { x_4 + x_5 } \over 2 } = { { 52 + 54 } \over 2 } = 53 \]

4. ve 5. değerler toplamı 2’ye bölünür ve medyan değeri 53 bulunur.

Uygulama: Ağırlıkların listelendiği tablo aşağıda verilmiştir.

Ağırlık (kg)

Kişi Sayısı

Toplam (Σ)

Ağırlıkların medyan değerini bulunuz.

Ağırlık (X_i)

f_i

Σf_i

Toplam (Σ)

\[ \tilde X = { X_{ {(\Sigma f_i) + 1 } \over 2 } } = { X_{ { 49 + 1 } \over 2 } } = X_{25} = 75 \]

Medyan frekansının (X₂₅) içinde bulunduğu birikimli frekans grubuna denk gelen gözlem değeri aynı zamanda frekans serisinin medyanıdır.

Uygulama: Boy uzunluklarının listelendiği tablo aşağıda verilmiştir.

Boy (cm)

Kişi Sayısı

165

170

175

180

185

Toplam (Σ)

Boy uzunluklarının medyan değerini bulunuz.

Boy (x_i)

f_i

Σf_i

165

170

175

180

185

Toplam (Σ)

Frekans toplamı çift sayı olduğu için

\[ \tilde x = { { x_{ \Sigma f_i \over 2 } + x_{ { \Sigma f_i \over 2 } + 1 } } \over 2 } = { { x_{ 20 \over 2 } + x_{ { 20 \over 2 } + 1 } } \over 2 } = { { x_{10} + x_{11} } \over 2 } = { { 175 + 180 } \over 2 } = 177.5 \approx 178 \text{ cm} \]

Birikimli frekans içerisinde 10. ve 11. sıraya karşılık gelen boy uzunlukları toplanır ve 2’ye bölünür. Elde edilen değer frekans serisinin medyan değeridir.

Uygulama: Sınav notları aşağıdaki tabloda gruplandırılmıştır.

Sınav Notu

Öğrenci Sayısı

00 - 20

20 - 40

40 - 60

60 - 80

80 - 100

Toplam (Σ)

100

Notların medyan değerini bulunuz.

Sınav Notu (X_i)

f_i

Σf_i

00 - 20

20 - 40

40 - 60

60 - 80

80 - 100

100

Toplam (Σ)

100

\[ \tilde X = \text{Low}_\text{med} + { { { \Sigma f_i \over 2 } - { \text{f}_\text{medPre} } }\over \text{f}_\text{med} } * \text{ClassInt} \]

Low_med: Birikimli frekanslar içerisinde (Σfi)/2 = 100/2 = 50. sıraya denk gelen 60 – 80 aralığının alt değeri 60’dır.
f_medPre: Medyan sınıfından bir önceki sınıfa kadar olan frekanslar toplamı (44)
f_med: Medyan sınıfının frekans değeri (43)
ClassInt: Sınıf aralığı (80 – 60 = 20)

\[ \tilde X = { 60 + { { { 100 \over 2 } - { 44 } }\over 43 } * 20 } = 62.79 \approx 63 \text{ puan} \]

Mod

Mod (Mode) seride en çok tekrar eden değerdir. Çift tepeli gruplandırılmış serilerde ve frekans serilerinde mod hesaplanamamaktadır. Gruplandırılmış serilerde gruplandırmanın daraltılması gerekmektedir.

Anakütle ve Örneklem Modu

Basit Serilerde

\[ \text{Mod} = \text{En Cok Tekrar Eden Deger} \]

Frekans Serilerinde

\[ \text{Mod} = \text{En Cok Tekrar Eden Frekans Sınıfı} \]

Gruplandırılmış Serilerde

\[ \text{Mod} = \text{Low}_\text{mod} + { \Delta_{1} \over { \Delta_{1} + \Delta_{2} } } * \text{ClassInt} \]

Low_mod: Mod sınıfının alt değeri (En çok frekansa sahip grup, mod sınıfıdır.)
Δ₁: Mod Sınıfı Frekansı – Mod Sınıfından Bir Önceki Sınıfın Frekansı
Δ₂: Mod Sınıfı Frekansı – Mod Sınıfından Bir Sonraki Sınıfın Frekansı
ClassInt (Class Interval): Sınıf aralığı

Excel’de mod almak için
=ENÇOK_OLAN.TEK() formülünü kullanabiliriz.

Uygulama: X₁ = 12, 14, 14, 16, 18, 18, 18, 18, 18, 20, 24 serisinin mod değerini bulunuz.

Seride en çok tekrar eden 18 olduğu için serinin modu 18’dir.

Uygulama: Boy uzunluklarının listelendiği tablo aşağıda verilmiştir.

Boy (cm)

Kişi Sayısı

165

170

175

180

185

Toplam (Σ)

Boy uzunluklarının mod değerini bulunuz.

En çok tekrar eden frekansa sahip grup 180 cm boy uzunluğu sınıfı olduğu için mod değeri 180’dir.

Uygulama: Sınav notları aşağıdaki tabloda gruplandırılmıştır.

Sınav Notu

Öğrenci Sayısı

00 - 20

20 - 40

40 - 60

60 - 80

80 - 100

Toplam (Σ)

100

Notların mod değerini bulunuz.

\[ \text{Mod} = \text{Low}_\text{mod} + { \Delta_{1} \over { \Delta_{1} + \Delta_{2} } } * \text{ClassInt} \]

Low_mod: Mod sınıfının alt değeri (En çok frekansa sahip grup, mod sınıfıdır.)
Δ₁: Mod Sınıfı Frekansı – Mod Sınıfından Bir Önceki Sınıfın Frekansı
Δ₂: Mod Sınıfı Frekansı – Mod Sınıfından Bir Sonraki Sınıfın Frekansı
ClassInt (Class Interval): Sınıf aralığı

En çok frekansa sahip grup 60 – 80 nota sahip aralıktır. Bu sebeple bu sınıf aynı zamanda mod sınıfıdır.

\[ \text{Mod} = 60 + { {(43 - 24)} \over { (43 - 24) + (43 - 13) } } * (80 - 60) = 67.76 \approx 68 \text{ puan} \]

Kartil

Kartil (Quartile) ya da Dörttebirlik seriyi dört eşit parçaya ayıran değerlerdir.

Anakütle Kartilleri

Basit Serilerde

\[ Q_1 = X_{ {N+2} \over 4} \]

Gözlem Sayısının Tek Olduğu Basit Serilerde

\[ Q_2 = \tilde X = X_{ {N+1} \over 2} \]

Gözlem Sayısının Çift Olduğu Basit Serilerde

\[ Q_2 = \tilde X ={ { X_{ {N} \over 2} } + { X_{ { {N} \over 2} + 1 } } \over 2 } \]

\[ Q_3 = X_{ {3N+2} \over 4} \]

\[ Q_4 = \text{Serinin Son Elemanı} \]

Frekans Serilerinde

\[ Q_1 = X_{ { {\Sigma f_i} + 2 } \over 4} \]

Frekans Toplamının Tek Sayı Olduğu Frekans Serilerinde

\[ Q_2 = \tilde X = { X_{ { \Sigma f_i} + 1 } \over 2 } \]

Frekans Toplamının Çift Sayı Olduğu Frekans Serilerinde

\[ Q_2 = \tilde X = { { X_{ \Sigma f_i \over 2 } + X_{ { \Sigma f_i \over 2 } + 1 } } \over 2 } \]

\[ Q_3 = X_{ { {3\Sigma f_i} + 1 } \over 4} \]

\[ Q_4 = \text{Serinin Son Elemanı} \]

Gruplandırılmış Serilerde

\[ Q_1 = \text{Low}_Q + { { { \Sigma f_i \over 4 } - f_ \text{QPre} \over f_Q } } * \text{ClassInt} \]

\[ Q_2 = \text{Low}_Q + { { { 2\Sigma f_i \over 4 } - f_ \text{QPre} \over f_Q } } * \text{ClassInt} = \tilde X \]

\[ Q_3 = \text{Low}_Q + { { { 3\Sigma f_i \over 4 } - f_ \text{QPre} \over f_Q } } * \text{ClassInt} \]

Low_Q:Kartil sınıfının alt değeri. (Q₁ Kartil Sınıfı= Σf_i/4, Q₂ Kartil Sınıfı= 2Σf_i/4, Q₃ Kartil Sınıfı= 3Σf_i/4)
f_QPre: Kartil sınıfından bir önceki sınıfa kadar olan frekanslar toplamı
f_Q: Kartil sınıfının frekansı
ClassInt (Class Interval): Sınıf aralığı

Kartil indisi ondalıklı ise en yakın tamsayıya tamamlanır. Ondalık .5 ise iki sayının ortalaması alınır.

Örneklem Kartilleri

Basit Serilerde

\[ Q_1 = x_{ {n+2} \over 4} \]

Gözlem Sayısının Tek Olduğu Basit Serilerde

\[ Q_2 = \tilde x = x_{ {n+1} \over 2} \]

Gözlem Sayısının Çift Olduğu Basit Serilerde

\[ Q_2 = \tilde x ={ { x_{ {n} \over 2} } + { x_{ { {n} \over 2} + 1 } } \over 2 } \]

\[ Q_3 = x_{ {3n+2} \over 4} \]

\[ Q_4 = \text{Serinin Son Elemanı} \]

Frekans Serilerinde

\[ Q_1 = x_{ { {\Sigma f_i} + 2 } \over 4} \]

Frekans Toplamının Tek Sayı Olduğu Frekans Serilerinde

\[ Q_2 = \tilde x = { x_{ { \Sigma f_i} + 1 } \over 2 } \]

Frekans Toplamının Çift Sayı Olduğu Frekans Serilerinde

\[ Q_2 = \tilde x = { { x_{ \Sigma f_i \over 2 } + x_{ { \Sigma f_i \over 2 } + 1 } } \over 2 } \]

\[ Q_3 = x_{ { {3\Sigma f_i} + 1 } \over 4} \]

\[ Q_4 = \text{Serinin Son Elemanı} \]

Gruplandırılmış Serilerde

\[ Q_1 = \text{Low}_Q + { { { \Sigma f_i \over 4 } - f_ \text{QPre} \over f_Q } } * \text{ClassInt} \]

\[ Q_2 = \text{Low}_Q + { { { 2\Sigma f_i \over 4 } - f_ \text{QPre} \over f_Q } } * \text{ClassInt} = \tilde X \]

\[ Q_3 = \text{Low}_Q + { { { 3\Sigma f_i \over 4 } - f_ \text{QPre} \over f_Q } } * \text{ClassInt} \]

Low_Q:Kartil sınıfının alt değeri. (Q₁ Kartil Sınıfı= Σf_i/4, Q₂ Kartil Sınıfı= 2Σf_i/4, Q₃ Kartil Sınıfı= 3Σf_i/4)
f_QPre: Kartil sınıfından bir önceki sınıfa kadar olan frekanslar toplamı
f_Q: Kartil sınıfının frekansı
ClassInt (Class Interval): Sınıf aralığı

Kartil indisi ondalıklı ise en yakın tamsayıya tamamlanır. Ondalık .5 ise iki sayının ortalaması alınır.

Excel’de kartil almak için
=DÖRTTEBİRLİK() formülünü kullanabiliriz.

Uygulama: X₁ = 12, 14, 14, 16, 18, 18, 18, 18, 18, 20, 24 serisinin kartil değerlerini bulunuz.

N: 11’dir. Gözlem sayısı tek sayı olduğu için

\[ Q_1 = X_{ {N+2} \over 4} = X_{ {11+2} \over 4} = X_{3.25} \approx X_3 = 14 \]

\[ Q_2 = \tilde X = X_{ {N+1} \over 2} = X_{ {11+1} \over 2} = X_6 = 18 \]

\[ Q_3 = X_{ {3N+2} \over 4} = X_{ {3*11+2} \over 4} = X_{8.75} \approx X_9 = 18 \]

\[ Q_4 = 24 \]

Uygulama: X₂ = 8, 24, 46, 46, 46, 48, 50, 52 serisinin kartil değerlerini bulunuz.

n: 8’dir.

\[ Q_1 = x_{ {n+2} \over 4 } = x_{ {8+2} \over 4 } = x_{2.50} \approx { {x_2 + x_3} \over 2 } = { {24 + 46} \over 2 } = 35 \]

Gözlem sayısı çift sayı olduğu için

\[ Q_2 = \tilde x ={ { x_{ {n} \over 2} } + { x_{ { {n} \over 2} + 1 } } \over 2 } ={ { x_{ {8} \over 2} } + { x_{ { {8} \over 2} + 1 } } \over 2 } = { { x_4 + x_5 } \over 2} = { {46 + 46} \over 2 } = 46 \]

\[ Q_3 = x_{ {3n+2} \over 4} = x_{ {3*11+2} \over 4} = x_{8.75} \approx x_9 = 18 \]

\[ Q_4 = 52 \]

Uygulama: Boy uzunluklarının listelendiği tablo aşağıda verilmiştir.

Boy (cm)

Kişi Sayısı

165

170

175

180

185

Toplam (Σ)

Boy uzunluklarının kartil değerlerini bulunuz.

\[ Q_1 = x_{ { {\Sigma f_i} + 2 } \over 4} = x_{ { 20 + 2 } \over 4} = x_{5.5} \approx x_5 =170 \text{ cm} \]

Frekans toplamı çift sayı olduğu için (Σf_i = 20)

\[ Q_2 = \tilde x = { { x_{ \Sigma f_i \over 2 } + x_{ { \Sigma f_i \over 2 } + 1 } } \over 2 } = { { x_{ 20 \over 2 } + x_{ { 20 \over 2 } + 1 } } \over 2 } = { { x_{10} + x_{11} } \over 2 } = { {175 + 180} \over 2 } = 177.5 \approx 178 \text{ cm} \]

\[ Q_3 = x_{ { {3\Sigma f_i} + 1 } \over 4} = x_{ { {3*20} + 1 } \over 4} = x_{15.25} \approx x_{15} = 180 \text{ cm} \]

\[ Q_4 = 185 \text{ cm} \]

Desil ve Persantil

Desil (Decile) seriyi 10, Persantil (Percentile) ise 100 eşit parçaya bölen değerlerdir.

Anakütle Desili

Basit Serilerde

\[ D_i = X_{ { iN + 2 } \over 10 } \]

Frekans Serilerinde

\[ D_i = X_{ { i\Sigma f_i + 2 } \over 10 } \]

Örneklem Desili

Basit Serilerde

\[ D_i = x_{ { in + 2 } \over 10 } \]

Frekans Serilerinde

\[ D_i = x_{ { i\Sigma f_i + 2 } \over 10 } \]

Anakütle Persantili

Basit Serilerde

\[ P_i = X_{ { iN + 2 } \over 100 } \]

Frekans Serilerinde

\[ P_i = X_{ { i\Sigma f_i + 2 } \over 100 } \]

Örneklem Persantili

Basit Serilerde

\[ P_i = x_{ { in + 2 } \over 100 } \]

Frekans Serilerinde

\[ P_i = x_{ { i\Sigma f_i + 2 } \over 100 } \]

Gruplandırılmış serilerde desil ve persantil hesaplanamamaktadır.

Excel’de persantil almak için
=YÜZDEBİRLİK(dizi;yüzde) formülünü kullanabiliriz.

yüzde parametresi 0 ve 1 arasında değer alır. Örneğin %12. persantili bulmak için 0,12 yazmalıyız.

Desilin formülü bulunmamaktadır.

Uygulama: x_d: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 serisinin 7. desilini ve 72. persantilini bulunuz.

Gözlem sayısı 10’dur. (n: 10)

\[ D_7 = x_{ { in + 2 } \over 10 } = x_{ { 7*10 + 2 } \over 10 } = x_{72 \over 10} = x_{7.2} \approx x_7 = 70 \]

\[ P_{72} = x_{ { in + 2 } \over 100 } = x_{ { 72*10 + 2 } \over 100 } = x_{722 \over 100 } = x_{7.22} \approx x_7 = 70 \]

Uygulama: Boy uzunluklarının listelendiği tablo aşağıda verilmiştir.

Boy (cm)

Kişi Sayısı

165

170

175

180

185

Toplam (Σ)

Boy uzunluklarının 8. dereceden desilini ve 67. dereceden persantilini bulunuz.

Boy (x_i)

f_i

Σf_i

165

170

175

180

185

Toplam (Σ)

\[ D_8 = x_{ { i\Sigma f_i + 2 } \over 10 } = x_{ { 8*20+2 } \over 10 } = x_{162 \over 10} = x_{16.2} \approx x_{16} = 180 \text{ cm} \]

\[ P_{67} = x_{ { i\Sigma f_i + 2 } \over 100 } = x_{ { 67*20+2 } \over 100 } = x_{1342 \over 100} = x_{13.42} \approx x_{13} = 180 \text{ cm} \]

Düzeltilmiş Ortalama

Düzeltilmiş Ortalama serinin başındaki ve sonundaki aykırı değerlerin etkisini azaltan özel bir ortalama türüdür.

Anakütle ve Örneklem Düzeltilmiş Ortalaması

\[ \text{Duzeltilmis Ort} = { {Q_1 + 2Q_2 + Q_3} \over 4 } \]

Uygulama: x_a = 2, 4, 4, 22, 23, 24, 24, 24, 26, 26, 26, 28, 28, 112, 114, 118 serisinin düzeltilmiş ortalamasını bulunuz.

Seri geneli itibariyle 22 ve 28 arasında dağılmaktadır. Aritmetik ortalamanın bu iki değer arasında olması beklenir. Fakat 37.81 bulunmuştur. Bu sebeple aritmetik ortalama yerine düzeltilmiş ortalama kullanılması daha uygundur.

Gözlem sayısı n: 16’dır.

\[ Q_1 = x_{ {n+2} \over 4} = x_{ {16+2} \over 4} = x_{4.5} = { {x_4 + x_5} \over 2 } = { {22 + 23 } \over 2 } \approx 22.5 = 23 \]

Gözlem sayısı çift olduğu için

\[ Q_2 = \tilde x ={ { x_{ {n} \over 2} } + { x_{ { {n} \over 2} + 1 } } \over 2 } ={ { x_{ {16} \over 2} } + { x_{ { {16} \over 2} + 1 } } \over 2 } = { { x_8 + x_9 } \over 2 } = { {24 + 26} \over 2 } = { 50 \over 2 } = 25 \]

\[ Q_3 = x_{ {3n+2} \over 4} = x_{ {3*16+2} \over 4} = x_{12.5} \approx x_{13} = 28 \]

\[ \text{Duzeltilmis Ort} = { {Q_1 + 2Q_2 + Q_3} \over 4 } = { {23 + 2*25 + 28} \over 4 } = { 101 \over 4 } = 25.25 \approx 25 \]

Beklenildiği gibi düzeltilmiş ortalama 22 - 28 arasındadır. İstatistiksel olarak seriyi aritmetik ortalamaya göre daha anlamlı temsil etmektedir.

Kırpılmış Ortalama

Kırpılmış Ortalama (trimmed mean, trimmean, truncated mean) serinin başındaki ve sonundaki belirli bir yüzdenin seriden atılarak hesaplanması ile elde edilen ortalamadır.

Uygulama: x_b = 1, 1, 2, 4, 4, 22, 23, 24, 24, 24, 26, 26, 26, 28, 28, 112, 114, 118, 120, 120 serisinin %50 düzeyinde düzeltilmiş ortalamasını bulunuz. (n: 20)

Seride 20 gözlem değeri vardır. %50’si (20 x %50) 10 etmektedir. Serinin başından 5 ve sonundan 5 olmak üzere toplam 10 değer atılır ve kırpılmış seri oluşturulur.

x_b = 1, 1, 2, 4, 4, 22, 23, 24, 24, 24, 26, 26, 26, 28, 28, 112, 114, 118, 120, 120

x_(trimmed)b = 22, 23, 24, 24, 24, 26, 26, 26, 28, 28

\[ \bar x_{(trimmed)b} = {\Sigma x_i \over n} = {251 \over 10 } = 25.1 \approx 25 \]

Excel’de kırpılmış ortalama almak için
=KIRPORTALAMA(dizi;yüzde) formülünü kullanabiliriz.

yüzde parametresi 0 ve 1 arasında değer alır. Örneğin %50 düzeyinde kırpılmış ortalama hesaplamak için yüzde parametresine 0,50 yazmalıyız.

SPSS'te Duyarlı Olmayan Ortalamalar

Mod, Medyan, Kartil

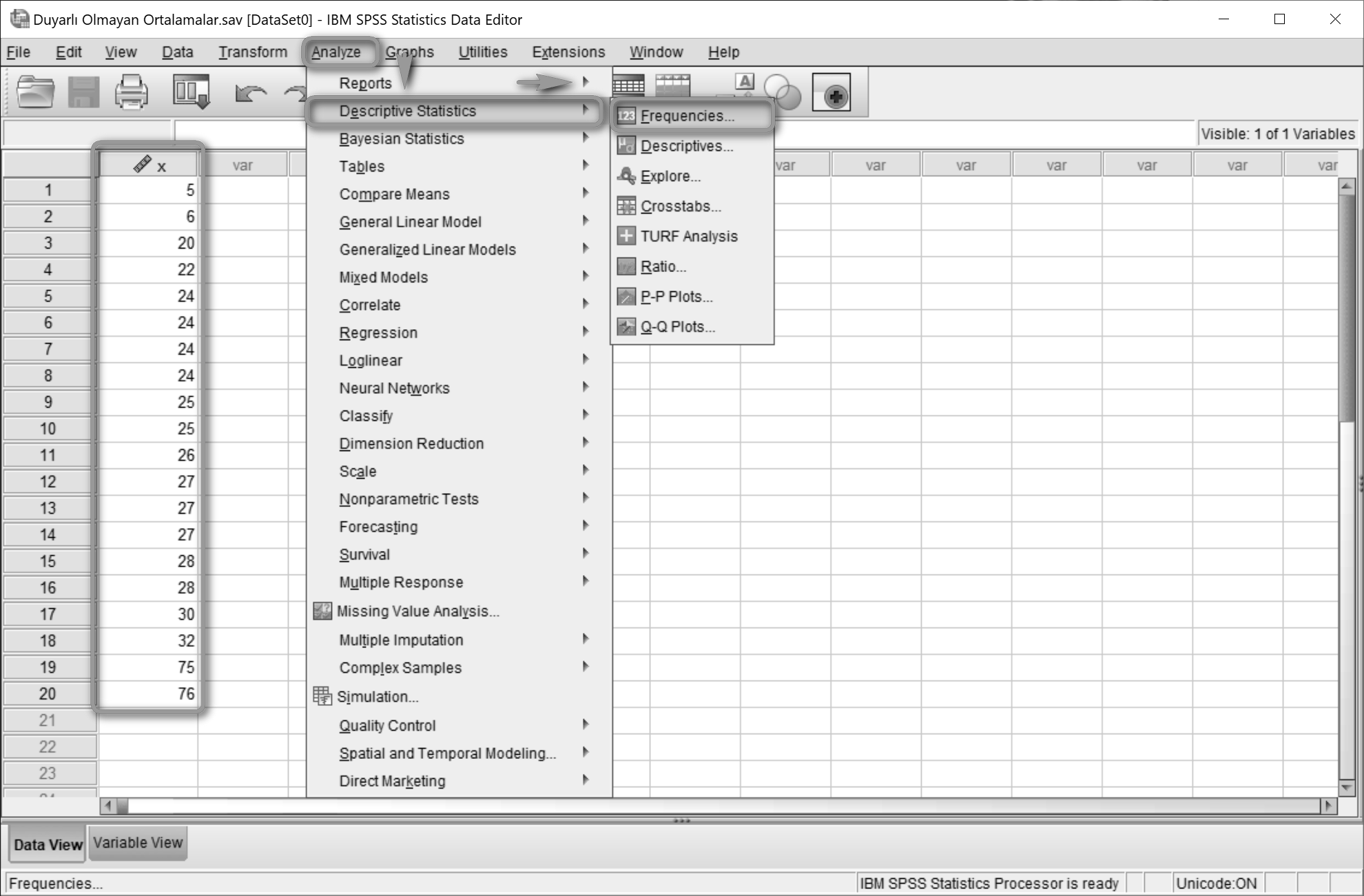
Elimizde 5’ten 76’ya kadar olan basit bir seri olduğunu varsayalım.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

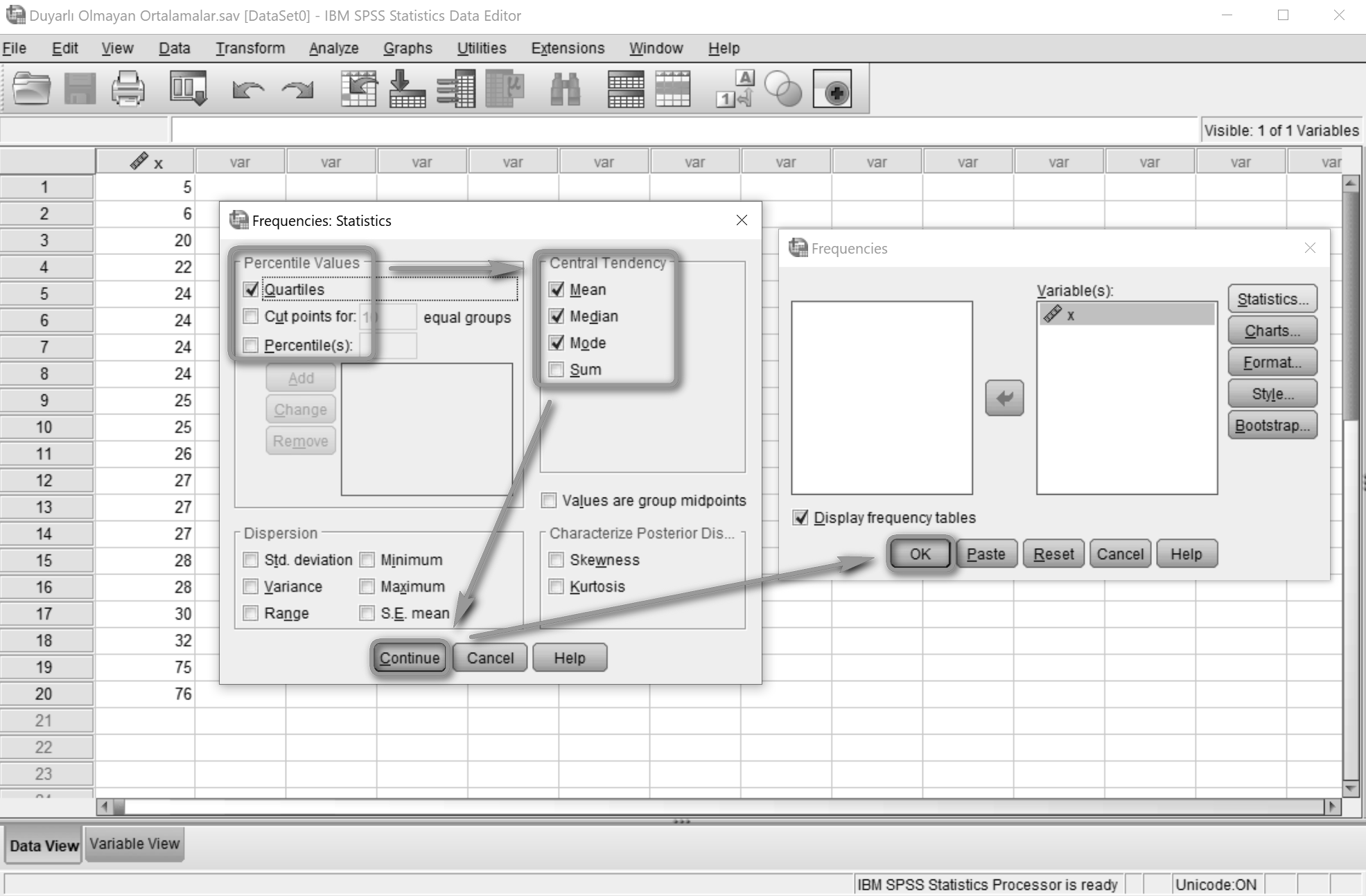
Analyze > Descriptive Statistics > Frequencies… yolu izlenir.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

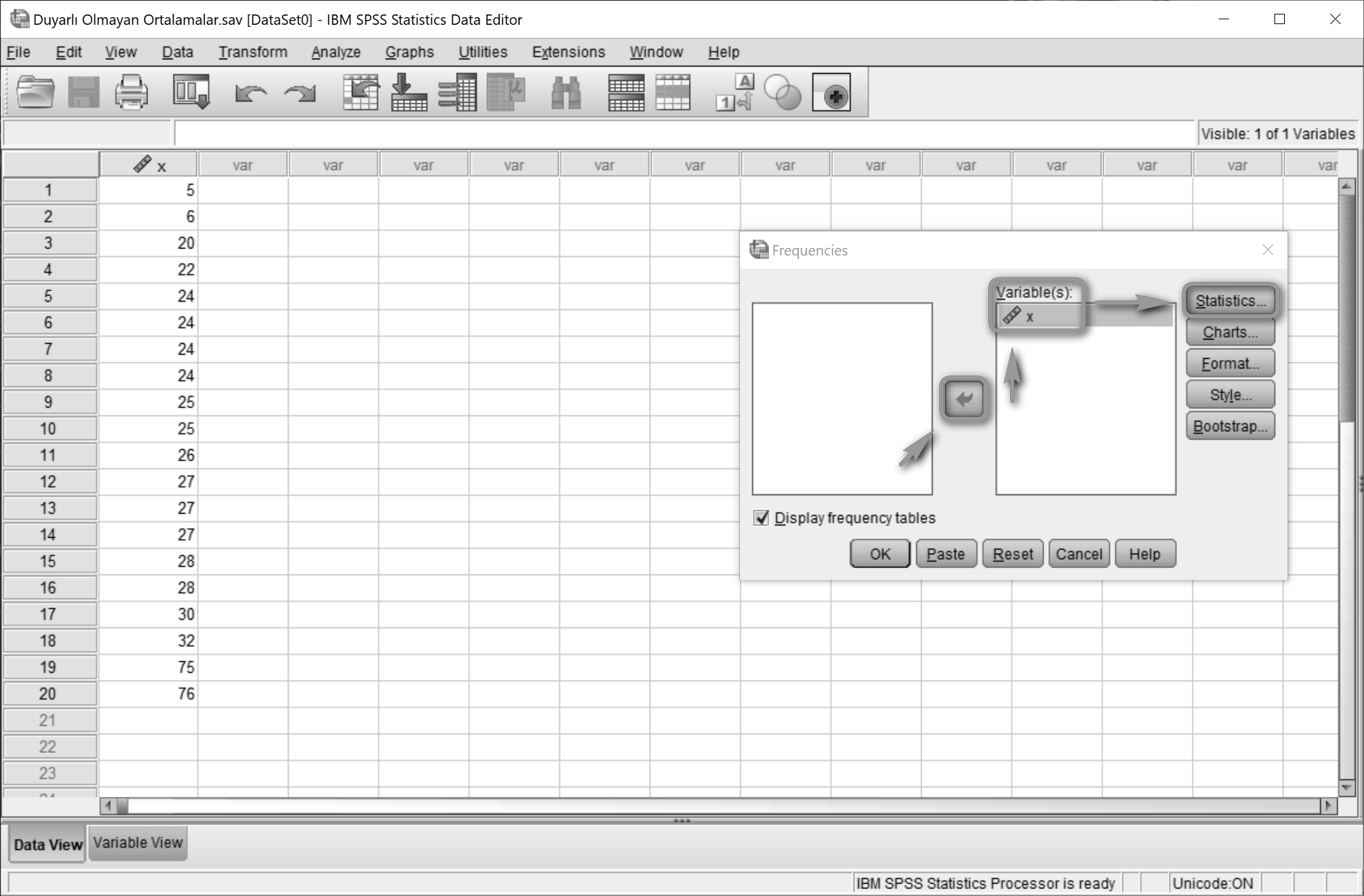
Seri, Variable(s) alanına aktarılır ve Statistics...’e tıklanır.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

Quartiles (kartiller), Mean (aritmetik ortalama), Median (medyan) ve Mode (mod) seçimleri yapılır.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

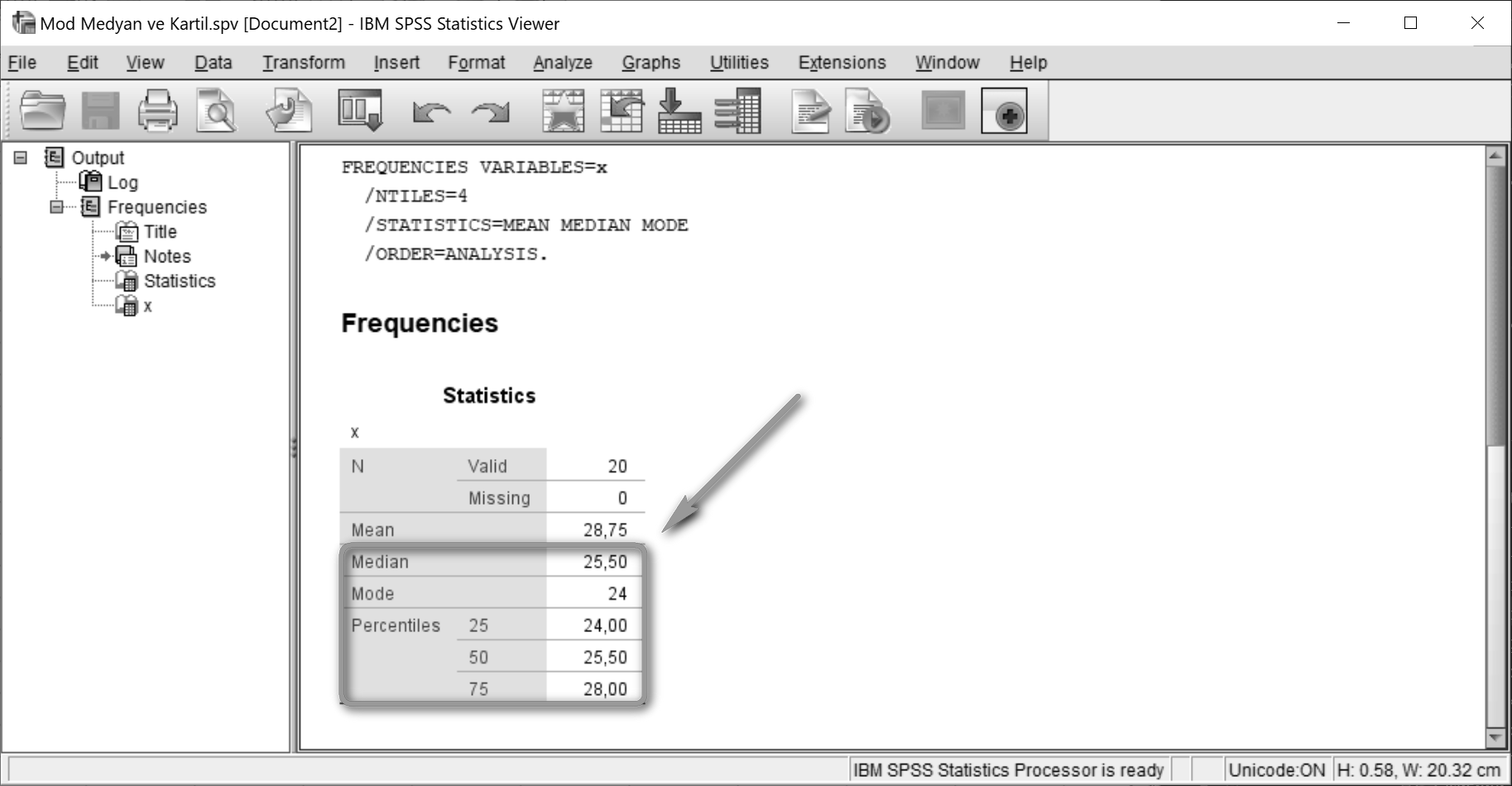
Mod (mode), medyan (median) ve kartil (quartile) değerleri görseldeki gibi listelenir.

Percentiles (25) Q1, Percentiles (50) Q2, Percentiles (75) ise Q3 kartilini belirtmektedir.

Desil ve Persantil

Mod, medyan ve kartil hesaplamasında kullandığımız serinin 8. desilini ve 75. persantilini hesaplamak isteyelim.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

Analyze > Descriptive Statistics > Frequencies… yolu izlenir.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

Seri, Variable(s) alanına aktarılır ve Statistics...’e tıklanır.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

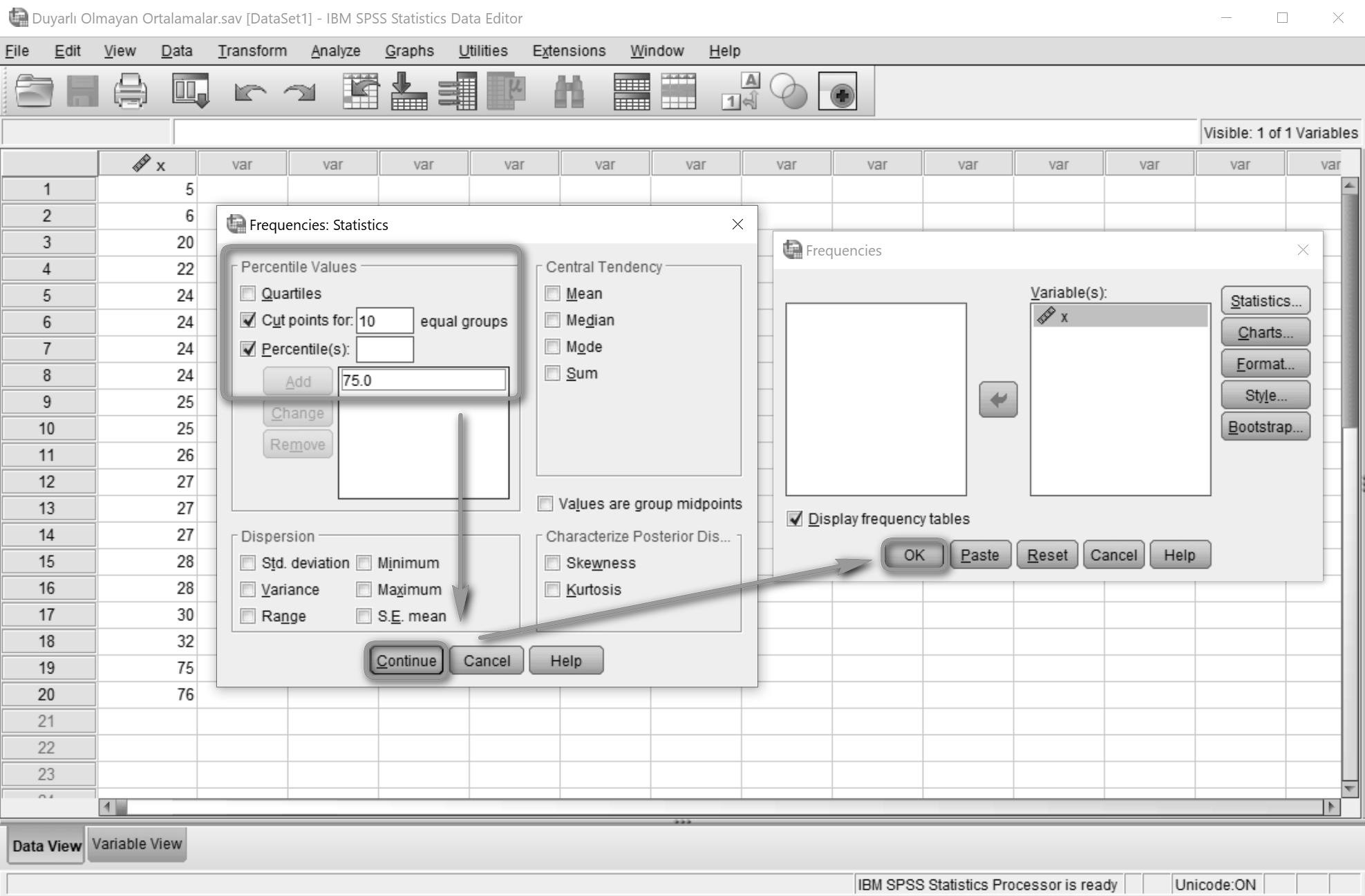
Açılan pencerede Cut points for alanına 10 yazılır. Bu şekilde tüm desil değerleri listelenecektir.

Percentile(s) alanına 75 yazılır ve Add düğmesi ile kutucuğa eklenir.

Büyütmek için görselin üzerine geliniz ya da tıklayınız.

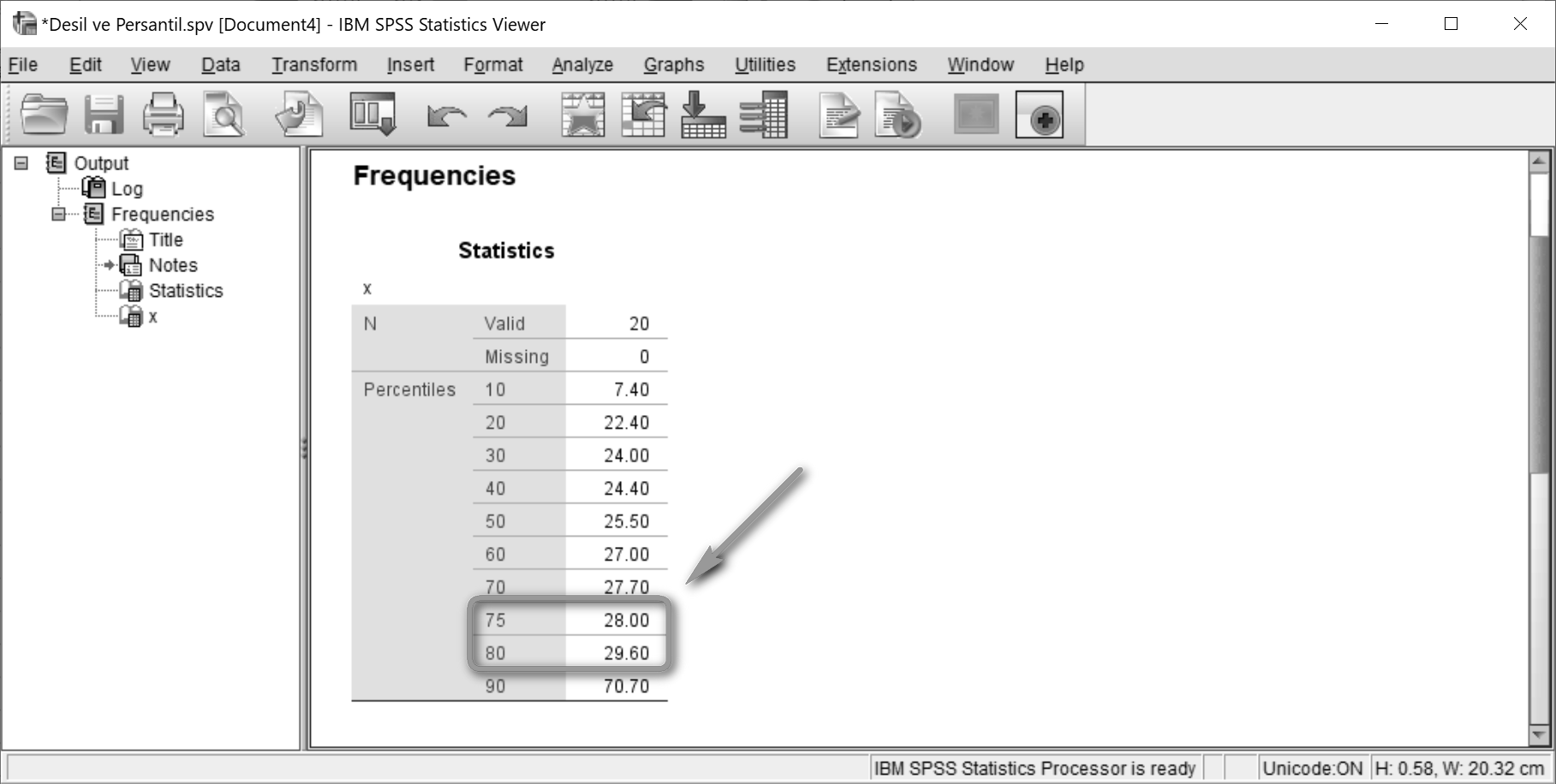
Percentiles alanında

75’e denk gelen değer 75. persantili (P₇₅)
80’e denk gelen değer ise 8. desili (D₈)

belirtmektedir.

Sıra Sizde

Uygulama: Bir sınıftan seçilen 8 öğrencinin sınav notları aşağıda verilmiştir.

\[ x = 55, 60, 70, 75, 80, 85, 85, 90 \]

Notların aritmetik ortalamasını bulunuz.

Yanıtı Göster

Seride 8 değer vardır. (n=8)

\[ \bar x = {\Sigma x_i \over n} \] \[ \bar x = {55 + 60 + 70 + 75 + 80 + 85 + 85 + 90 \over 8} = 75 \]

Sınav notlarının aritmetik ortalaması 75 bulunur.

Uygulama: Bir sınıftan seçilen 6 öğrencinin sınav notları aşağıda verilmiştir.

\[ x = 4, 68, 70, 70, 72, 96 \]

Notların geometrik ortalamasını bulunuz.

Yanıtı Göster

Seride 6 değer vardır. (n=6)

\[ \text{Log Geo Ort} = {\Sigma logx_i \over n} \] \[ \text{Log Geo Ort} = {log(4) + log(68) + log(70) + log(70) + log(72) + log(96) \over 6} \] \[ \text{Log Geo Ort} = 9.9644/6 = 1.6607 \] \[ \text{AntiLog Geo Ort} = \text{Geo Ort} = 45.78 \approx 46 \]

Sınav notlarının geometrik ortalaması 46 bulunur.

Uygulama: Aşağıda 7 birimden oluşan örneklem listelenmiştir.

\[ x = 44, 46, 48, 48, 50, 52, 112 \]

Örneklemin harmonik ortalamasını bulunuz.

Yanıtı Göster

Seride 7 değer vardır. (n=7)

\[ \text{Hrm Ort} = {n \over \Sigma {1 \over x_i}} = {7 \over {1 \over 44} + {1 \over 46} + {1 \over 48} + {1 \over 48} + {1 \over 50} + {1 \over 52} + {1 \over 112}} \] \[ \text{Hrm Ort} = 7/0.1344 = 52.13 \approx 52 \]

Örneklemin harmonik ortalaması 52 bulunur.

Uygulama: Aşağıda 12 birimden oluşan örneklem serisi listelenmiştir.

\[ x = 4, 4, 8, 12, 12, 12, 12, 16, 18, 20, 24, 28 \]

Serinin medyanını (ortanca değerini) bulunuz.

Yanıtı Göster

Gözlem sayısının çift olduğu basit serilerde medyan değeri aşağıdaki gibi hesaplanır.

\[ \tilde x = { { x_{n\over 2} } + { x_{ { n\over 2}+1 } } \over 2} \] \[ \tilde x = { { x_{12\over 2} } + { x_{ { 12\over 2}+1 } } \over 2} \] \[ \tilde x = { { x_6 } + { x_7 } \over 2} \] \[ \tilde x = { { 12 } + { 12 } \over 2} \] \[ \tilde x = { 24 \over 2} \] \[ \tilde x = { 12 } \]

Serinin medyan değeri 12 bulunur.

Uygulama: Aşağıda 12 birimden oluşan örneklem serisi listelenmiştir.

\[ x = 4, 4, 8, 12, 12, 12, 12, 16, 18, 20, 24, 28 \]

Serinin mod'unu (tepe değerini) bulunuz.

Yanıtı Göster

Seride en çok tekrar eden değer 12 olduğu için serinin modu 12'dir.

Uygulama: Aşağıda 12 birimden oluşan örneklem serisi listelenmiştir.

\[ x = 4, 4, 8, 12, 12, 12, 12, 16, 18, 20, 24, 28 \]

Serinin 3. dereceden kartilini (Q₃'ü) bulunuz.

Yanıtı Göster

\[ Q_3 = x_{ {3n+2} \over 4} \] \[ Q_3 = x_{ {3(12)+2} \over 4} \] \[ Q_3 = x_{ {38} \over 4} \] \[ Q_3 = x_{9.50} \] \[ Q_3 = { { x_9 } + { x_{10} } \over 2} \] 9. ve 10. sıradaki birimler 18 ve 20'dir. \[ Q_3 = { 18 + 20 \over 2} \] \[ Q_3 = 19 \]

Serinin 3. dereceden kartili (Q₃'ü) 19 bulunur.

1 Aykırı değer (outlier)
2 Ortalama Gelir, Medyan Gelir ve Gini Katsayısı örneği için tıklayınız.
3 IBM SPSS Statistics | version 26.0.0.0
4 Değişken(ler)
5 Seçenekler
6 Ortalama

<<< Önceki Konu

Sonraki Konu >>>