İstatistik derslerini tablet üzerinden çalışmanız şiddetle tavsiye olunur.

Verilerin Derlenmesi ve Düzenlenmesi

Araştırmaya başlanılmadan önce edinilen ham verilerin kirli verilerden temizlenmesi konusuna değinmiştik. Ham veriler kirli veriler içermese bile veri setini okunaklı hâle getirmek için bazı düzenlemelere ihtiyaç duyarız.

Veri modellemesinde “Verilerin Toplanması” (Collecting Data) aşamasının ardından “Verilerin Derlenmesi ve Düzenlenmesi” (Compiling & Organizing Data) aşamalarına geçilir. Veriler türlerine göre derlendikten sonra veri setini “sınıflama ve gruplama metodları” ile özet tablolara dönüştürürüz.

Verilerin Toplanması

Elimizde 122 öğrencinin istatistik sınav notlarını temsil edecek 44 öğrenciye ait 4 farklı sınıfın verisi olsun.

\[ x_1 = 48, 45, 48, 64, 50, 24, 04, 12, 88, 71, 64\] \[ x_2 = 24, 12, 25, 33, 44, 45, 64, 48, 55, 64, 88\] \[ x_3 = 12, 24, 25, 48, 64, 88, 88, 71, 48, 55, 50\] \[ x_4 = 74, 48, 64, 88, 24, 12, 04, 71, 55, 48, 50\]

Verilerin Derlenmesi ve Özetlenmesi

Tek bir veri setinde tüm verileri küçükten büyüğe sıralarsak aşağıdaki seriyi elde ederiz.

\[ x = 04, 04, 12, 12, 12, 12, 24, 24, 24, 24, 25, 25, 33, 44, 45, 45, 48,\] \[ 48, 48, 48, 48, 48, 48, 50, 50, 50, 55, 55, 55, 64, 64, 64, 64, 64, 64,\] \[ 71, 71, 71, 74, 88, 88, 88, 88, 88\]

Serinin az sayıda birimden oluşmasından ve tek bir değişken içermesinden dolayı derleme aşaması tamamlanmıştır.

Dikkatli bakıldığında veri setinin tekrar eden sayılardan oluştuğu görülebilir. Hangi sayıların hangi sıklıkla tekrar edildiğini görebilmek için birimleri sınıflandırabiliriz.

f (tekrar sayısı)

Toplam (Σ)

Bu noktada sınavda 48, 64 ve 88 not alan öğrencilerin çoğunlukta olduğu sonucuna varabiliriz. Yaptığımız işleme “sınıflama” (statistical classification) denilmektedir. f notasyonu¹, birimlerin veri setinde hangi sıklıkla tekrar edildiğini belirtmektedir.

Tabloyu biraz daha özet hâle getirelim.

Sınıf Aralığı

Frekans (f)

00 - 25

26 - 50

51 - 75

76 - 100

Toplam (Σ)

Bu işleme ise gruplandırma ya da gruplama (statistical grouping) denilmektedir. Gruplandırma, sınıf dağılımlarının özet tablolara dönüştürülmesi işlemidir. Örnekte istatistik dersinden alınan notların 0 ve 75 arasında yoğunlaştığı görülebilir.

Verilerin Grafikleştirilmesi

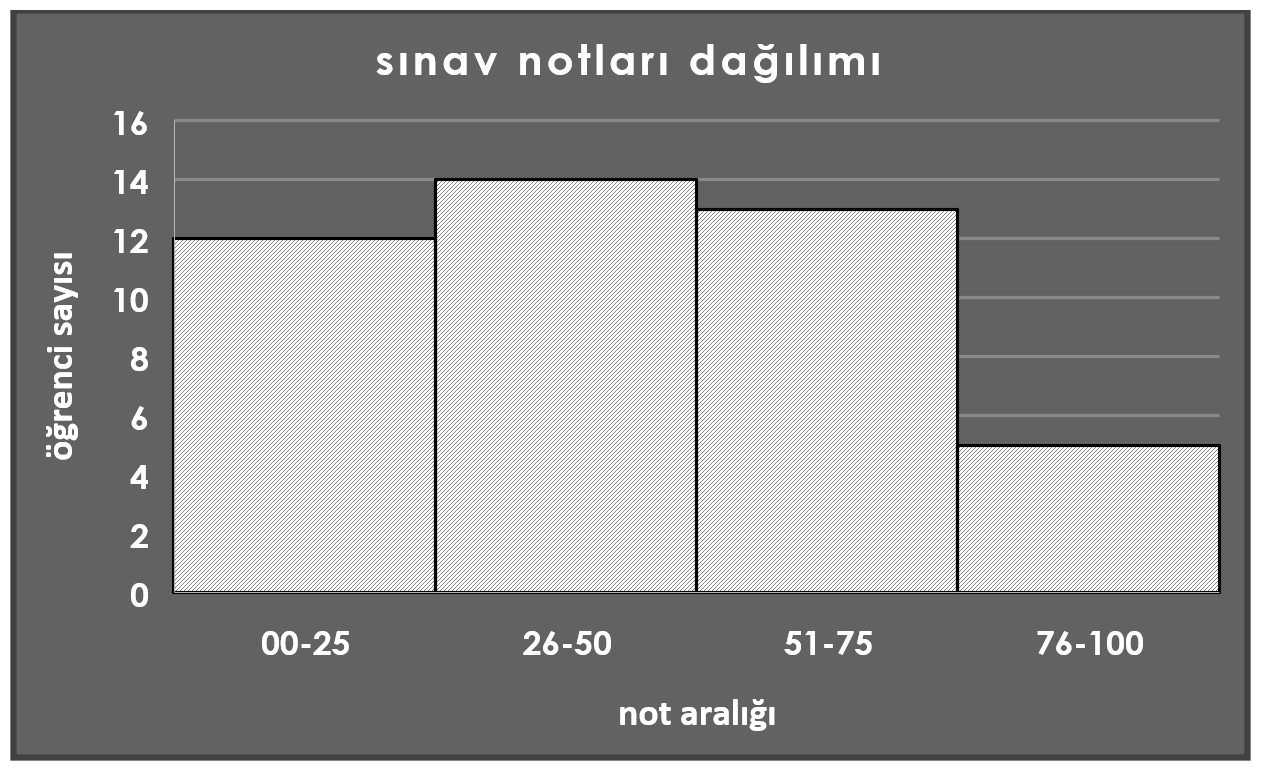
Yoğunlaşmayı net görebilmek için histogram grafikleri kullanırız. (Yukarıdaki grafik histogram grafiğidir.)

Bu tür basit örneklerde sınıf aralığı ve birim sayısının az olmasından dolayı grafik kullanmamıza bile gerek bulunmamaktadır. Buna rağmen çok fazla verinin ve sınıf aralığının olduğu veri setlerinde grafik kullanılması yoğunlaşmanın nerede olduğunu anlamamızda tablolara göre daha fazla esneklik sağlayacaktır.

Gruplandırmada Sınıf Aralığı Uzunluğunun Belirlenmesi

İstatistik sınav notları örneğinde sınıf aralığını 25 notluk dilimlere ayırarak 4 farklı dilimde belirledik. Sınıfları aralıklandırmayı, diğer bir ifade ile gruplandırmayı tamamen kendi yöntemlerimizle gerçekleştirdik.

İstatistik standartlarına uygun gruplandırma yapmak istersek sınıf aralığını aşağıdaki formül ile belirleriz.

\[ \text{Sınıf Aralıgı} = [x_{max} - x_{min}]/[1+3.3log(n)] \] \[ \text{Sınıf Aralıgı} = \text{Sınıf Uzunlugu (Range)}/\text{Sınıf Sayısı} \]

\[ x = 04, 04, 12, 12, 12, 12, 24, 24, 24, 24, 25, 25, 33, 44, 45, 45, 48,\] \[ 48, 48, 48, 48, 48, 48, 50, 50, 50, 55, 55, 55, 64, 64, 64, 64, 64, 64,\] \[ 71, 71, 71, 74, 88, 88, 88, 88, 88\]

x_max: En yüksek değer
x_min: En düşük değer
n: Birim sayısı

Formülü x serisine uyguladığımızda

\[ \text{Sınıf Aralıgı} = [x_{max} - x_{min}]/[1+3.3log(n)] \] \[ \text{Sınıf Aralıgı} = [88 - 04]/[1+3.3log(44)] \] \[ \text{Sınıf Aralıgı} \approx 13.08 \approx 13 \]

Sınıf Aralığı

Frekans (f)

04 ≤ x < 17

17 ≤ x < 30

30 ≤ x < 43

43 ≤ x < 56

56 ≤ x < 69

69 ≤ x < 82

82 ≤ x < 95

Toplam (Σ)

Dikkat edilirse ilk aralığımız olan 04 ≤ x < 17 aralığının uzunluğu
17 – 04 = 13’tür. “Sınıf aralığı” ifadesi buradan gelmektedir.

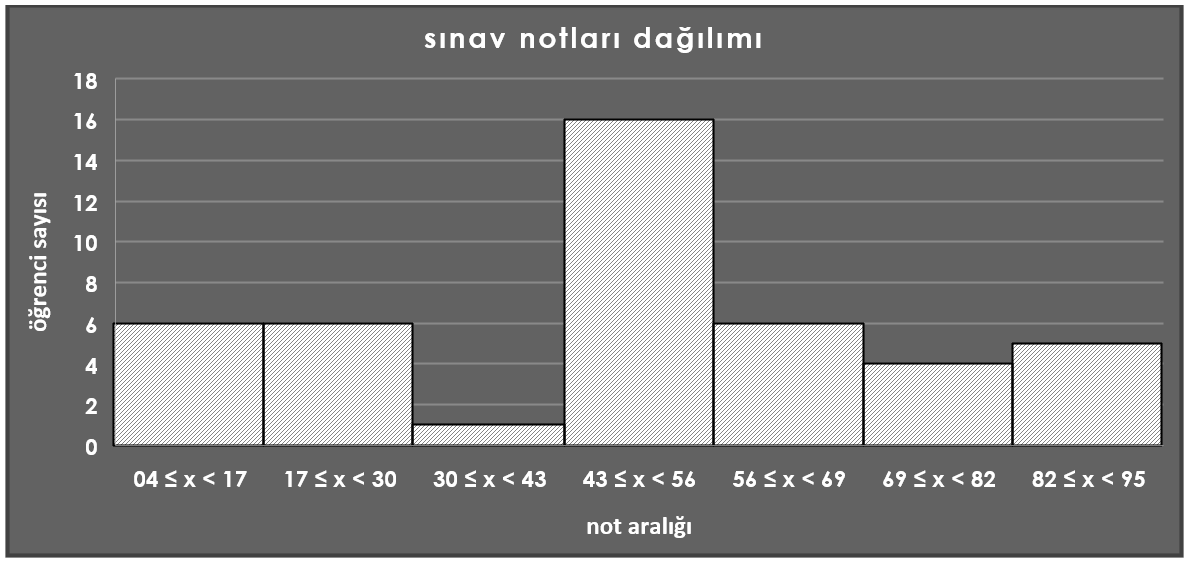
Bir önceki histogram grafiğinden farklı olarak sınav notlarının 43 ve 56 aralığında yoğunlaştığını rahatlıkla söyleyebilir, “44 öğrencinin 16’sı
43 ≤ x < 56 aralığında not almıştır” sonucuna varabiliriz.

Göreceli ve Birikimli Frekans

Göreceli Frekans (Relatif Frekans, Relative Frequency): Frekans dağılımının yüzdesel gösterimidir.

Birikimli Frekans (Kümülatif Frekans, Cumulative Frequency): Frekans dağılımının birikimli gösterimidir.

Sınıf Aralığı

Frekans (f)

Gör. Frekans (%)

Bir. Frekans (Σf)

Gör. Bir. Fre. (%Σf)

04 ≤ x < 17

%13.64

17 ≤ x < 30

%13.64

%27.27

30 ≤ x < 43

%2.27

%29.55

43 ≤ x < 56

%36.36

%65.91

56 ≤ x < 69

%13.64

%79.55

69 ≤ x < 82

%9.09

%88.64

82 ≤ x < 95

%11.36

%100

Toplam (Σ)

%100

04 ≤ x < 17 aralığının göreceli frekansı hesaplanırken frekans sayısı frekans toplamına bölünür ve % (yüzde) ifadesi ile gösterilir.
(6/44 = 0.1364 = %13.64)

Birikimli frekansta bir önceki sınıf aralığının frekans sayısı toplanır ve sonraki sınıf aralığına geçilir.

0 + 6 = 6

6 + 6 = 12

12 + 1 = 13

...

Göreceli birikimli frekans, birikimli frekansın oransal gösterimidir.
43 ≤ x < 56 aralığının göreceli birikimli hesaplanırken birikimli frekans değeri frekans toplamına bölünür. Göreceli frekansta olduğu gibi % ifadesi ile gösterilir. (29/44 = %65.91)

Yorumlanmaları şu şekildedir:

44 öğrencinin %9’u 69 ≤ x < 82 aralığında not almıştır. (göreceli frekans)
04 ≤ x < 82 aralığında not alanların sayısı 39’dur. (birikimli frekans)
04 ≤ x < 82 aralığında not alanların örneklem içindeki payı %89’dur. (göreceli birikimli frekans)

Hatırlarsanız 122 öğrenciden 44 öğrenciyi örnekleme amacıyla seçmiştik. Bu sebeple “örneklem içindeki payı %89’dur” yorumlaması yerine “tüm öğrenciler içindeki payı %89’dur” sonucuna varmak istatistiksel olarak anlamlı olmazdı.

Herhangi bir istatistiksel kaynakta “göreceli” ya da “relatif” ifadeleri geçiyorsa “oransal” (nispî, proportional) değerlerden söz ediliyordur. Göreceli değerler çoğunlukla oransal (yüzdesel) artışları veya azalışları göstermek için kullanılır.

Yüzde (%) Gösterimleri ve Yuvarlamalar

% (yüzde) ifadeleri kendi notasyonu ile gösterilse de 0.1424 şeklinde ondalıklı da gösterilebilir. Kimi zaman ondalıklı değerler 100 ile çarpılır ve 14.24 gösterimleri tercih edilir. “Çarpı 100” gösterimlerinin tercih edilmesi durumunda sütun başlıklarında ifadenin oransal değer olduğu mutlaka belirtilmelidir. Sütun başlığının “Pay” yerine “Pay (%)” olması gibi …

İstatistikte 0 değeri sayıların başlangıcında kullanılmayabilir. Örneğin; “0.1424” oranını “.1424” şeklinde gösterebiliriz. “Nokta Sayı” gösterimleri noktadan önce 0 (sıfır) kullanıldığını belirtir.

Hesap makinenizde .1424 x 2 işlemini yaptığınızda sonucun 0.2848 olduğunu görebilirsiniz.

Yuvarlamalar (rounding) ondalık basamakların azaltılmasında kullanılan ve sayı okunurluğunu artıran özelliklerden biridir. Yuvarlamalarda son ondalığın 5 veya 5’ten yukarı olup olmadığına bakılır. 5 veya 5’ten yukarı ise bir üst sayıya tamamlanır. Değilse soldaki ondalıkta değişiklik yapılmaz.

0.142457329 = 0.14245733 = 0.1424573 = 0.142457 = 0.14246 = 0.1425 = 0.143 = 0.14 = 0.1

Sıra Sizde

Uygulama: x = 10, 10, 10, 11, 11, 16, 18, 20, 22, 22, 24 serisinin sınıf uzunluğu ve sınıf aralığı kaçtır?

A) Sınıf Uzunluğu: 10 | Sınıf Aralığı: 5
B) Sınıf Uzunluğu: 14 | Sınıf Aralığı: 3
C) Sınıf Uzunluğu: 10 | Sınıf Aralığı: 5
D) Sınıf Uzunluğu: 14 | Sınıf Aralığı: 3

Yanıtı Göster

Sınıf uzunluğunu x_max - x_min formülü ile bulabiliriz. Sınıf Uzunluğu = 24 - 10 = 14 olarak hesaplanır.

Sınıf aralığını ise aşağıdaki formül ile hesaplarız. Seride 11 veri birimi vardır. (n = 11)

\[ \text{Sınıf Aralıgı} = [x_{max} - x_{min}]/[1+3.3log(n)] \] \[ \text{Sınıf Aralıgı} = [24 - 10]/[1+3.3log(11)] \] \[ \text{Sınıf Aralıgı} \approx 3.1556 \approx 3 \]

Bu şekilde sınıf aralığını 3 buluruz.

1 frekans (frequency)

<<< Önceki Konu

Sonraki Konu >>>