İstatistik derslerini tablet üzerinden çalışmanız şiddetle tavsiye olunur.
İstatistik Kullanım Alanları ve Yöntemleri
Bu konuda istatistiğin kullanım alanlarına ve yöntemlerine değineceğiz.
İstatistiğin Kullanım Alanları
Veri bilimi gibi istatistik de disiplinler arası alandır. Astronomide astroistatistik, iktisatta ekonometri, kimyada kemometri, biyolojide biyoistatistik, psikolojide psikometri, sosyolojide sosyometri gibi bilim dallarının oluşmasını sağlamıştır. Günlük hayatta istatistiği görünür hâli ile kullandığımız gibi uzmanlık alanı gerektiren alanlarda istatistiğe daha fazla ihtiyaç duyarız. İstatistik elde ettiğimiz bulguları açıklamamıza, veriler yardımıyla genel ve özel sonuçlara ulaşmamıza yardımcı olur. Çok büyük bir veri seti üzerinde çalışılıyorsa yapılan örneklemeler ile zaman ve maliyet tasarrufu sağlanır.
İstatistiğin Yöntemleri
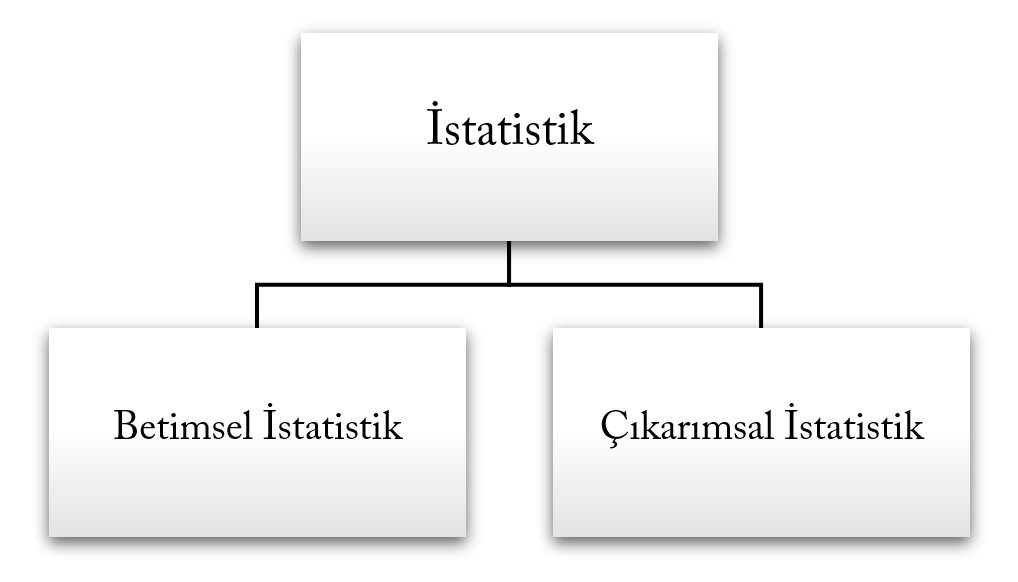
Betimsel İstatistik (descriptive statistics): Verilerin ortalamalar, standart sapmalar, grafikler ile özetlendiği, geçmişe yönelik yorumlandığı istatistik yöntemidir.
Çıkarımsal İstatistik (statistical inference): Verilerin hipotez testleri, varyans analizi, korelasyon analizi, regresyon analizi gibi tekniklerle hem geçmişe hem de geleceğe yönelik yorumlandığı istatistik yöntemidir.
İki yöntemin yanında az bilinen bir yöntem daha vardır. “Keşifsel Veri Analizi” adıyla tanımlanan bu metodda betimsel ve çıkarımsal istatistikte kullanılan tekniklerin grafikler yardımıyla özetlenmesi esastır. 1960’larda John Tukey tarafından literatüre kazandırılmıştır.
İleri Okuma
Keşifsel Veri Analizi
Veri madenciliğinde keşifsel veri analizi (exploratory data analysis, EDA), veri kümesi temel karakteristiğinin sıklıkla görsel metotlar yardımıyla özetlendiği yaklaşımdır. Modelleme aşamasından önce verinin bize ne göstermek istediğini anlamamızı sağlar. Tek bir sütundaki onlarca sayıya ya da tüm bir Excel sayfasına bakıp verinin tipik özelliklerini tanımlamak kolay değildir. Sadece sayılara bakıp veri hakkında çıkarsamalarda bulunmak zahmetli, bıktırıcı ve usandırıcı bir iş hâline dönüşebilir. Keşifsel veri analiz teknikleri bu gibi durumlara çözüm amacıyla geliştirilmiştir.
Keşifsel veri analizinde iki ana yöntemle çapraz sınıflandırma yapılır.1 İlkinde her bir metot ya grafikseldir ya da özet tablolardan oluşur. İkincisinde yöntemler tek değişkenli ya da çok değişkenli olmalıdır. (Çoğunlukla iki değişkenlidir.)

Keşifsel Veri Analizi Örneği
Keşifsel veri analizinin öğrenilmesini kolaylaştırmak adına “süsen veri seti”2 üzerinde çalışma yapacağız.
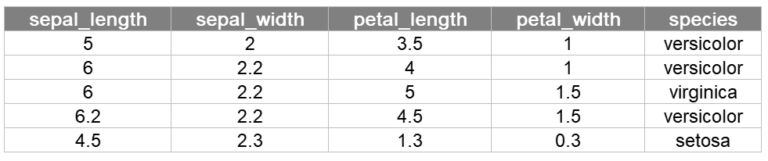
Veri seti, süsen çiçeğinin 3 farklı türüne3 ait 4 farklı özelliğini4 içermektedir. Veri kümesinde 50 farklı örnek (50 satır) olmakla birlikte 3 farklı tür ile toplamda 150 birim5 yer almaktadır.
Tek Değişken Analizi
Tek değişken analizi, verinin tek değişkenli olduğu durumlarda kullanılan en basit veri analizi uygulamasıdır. Sadece tek bir değişkene sahip olmasından dolayı neden – sonuç bağlarına ve bağımsız değişkenler arasındaki ilişkilere ihtiyaç duyulmaz. Temel amaç veriyi tanımlamak ve veriyi oluşturan yapıyı bulmaya çalışmaktır.
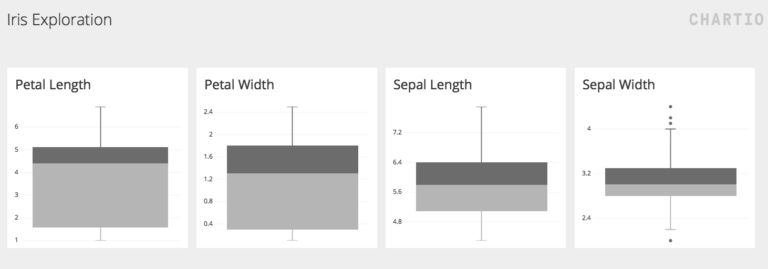
A. Kutu Diyagramı
Veri kümesini “beş gösterge” ile özetler: Minimum değer (Q0), ilk kartil (Q1), medyan (Q2), üçüncü kartil (Q3) ve maksimum değer (Q4).
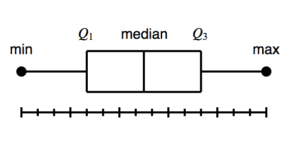
Oluşturulan diyagram veri setindeki dört nümerik özelliğin özetini verir. Kutuların büyüklüğünden taç (petal) uzunluk ve genişliklerinin çanağa (sepal’e) göre daha büyük olduğunu söyleyebiliriz. Buna rağmen çanak uzunluk ve genişlikleri medyan (ortanca) etrafında yoğunlaşmıştır. Dahası çanak genişliği diyagramında bulunan noktalardan aykırı değerlerin6 varlığını gözlemleyebiliriz.
B. Histogram
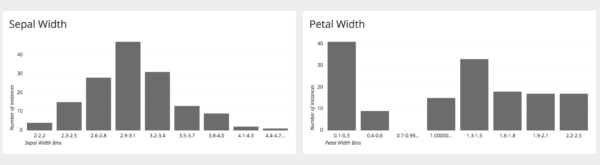
Sürekli değişkenler ile oluşturulan veri kümesine ait frekans dağılımını gösteren diyagramdır. Dağılımın normal dağılım olup olmadığını, dağılımdaki aykırı değerleri ve dağılıma ait çarpıklık derecesi gibi önemli özellikleri incelememize yarar.
Yukarıdaki diyagram, çanak ve taç genişliklerinin histogram grafiğini göstermektedir. Soldaki grafikte çanak genişliklerinin normal dağılıma sahip olduğu görülebilir. Buna rağmen ikinci grafikte taç genişlikleri sağa çarpık dağılım sergilemiştir. Ayrıca taç genişliklerine ait örneklerin büyük bölümü 0.4 cm’den daha kısadır.
Çok Değişken Analizi
Birden fazla değişken içeren verinin istatistiksel teknikler ile analizini belirtir. Gerçeğe daha yakın modellemeler yapmamızı sağlar.
A. Dağılım Grafiği
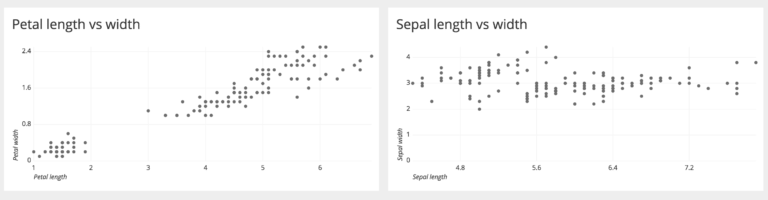
Dağılım grafiği iki farklı değişkenden elde edilen değerlerin X ve Y eksenlerine denk gelen kesişimlerini gösteren iki boyutlu veri görselleştirmesidir.
Yukarıdaki dağılım grafiklerinin ilkinde taç uzunluk ve genişlikleri arasında doğrusal bir ilişki olduğunu söyleyebiliriz. Buna rağmen çanak uzunlukları ile genişlikleri arasında orantısal bir artış olmamasından dolayı pozitif ya da negatif yönlü doğrusal bir ilişki olmadığı sonucuna varılabilir.
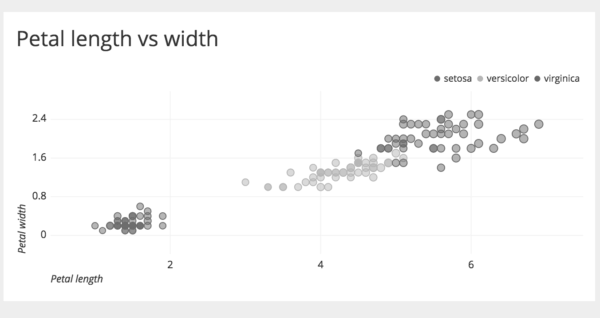
Dağılım grafiklerinin renkli gösterilmesi hâlinde diyagrama yeni değişkenler eklenebilir. Aşağıdaki örnekte çiçek türleri renklendirilerek üç türe ait taç uzunluk ve genişlikleri tek bir grafik üzerinde gösterilmiştir.
En küçük taç uzunluk ve genişlik değerlerine sahip çiçeğin setosa süseni, en büyük değerlere sahip çiçeğin ise virginya süseni olduğunu söyleyebiliriz. Çok renkli süsene ait taç uzunluk ve genişlikleri setosa ve virginya süsenlerinin arasındadır.
A. Sütun Grafiği
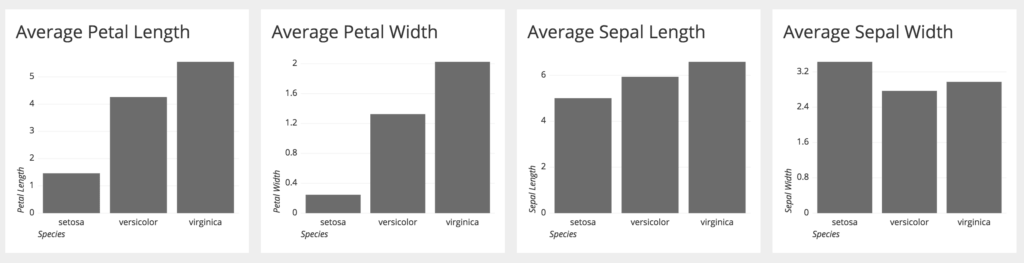
Kategorik verilere7 ait değerlerin oransal uzunluklarını gösteren grafik türüdür. Örneğin, veri setimizdeki tüm çiçek türlerine ait ortalama taç/çanak uzunluklarını ve genişliklerini görmek isteyelim.
Sütun grafiklerinden görebileceğimiz gibi virginya süseninin en büyük taç uzunluk ve genişliği ile çanak uzunluğuna sahip olduğunu söyleyebiliriz. Bununla birlikte setosa süseninin çanak genişliği genelden farklı olarak en yüksek değere sahiptir.
Örneğini incelediğimiz keşifsel veri analizi, verinin içeriğine dair iyi bir bakış açısına sahip olmamıza yarar. Keşifsel veri analizi aşaması tamamlandığında kümeleme8 ve sınıflandırma9 gibi daha karmaşık modelleme adımlarına geçilebilir.
Keşifsel veri analizi için örneklendirdiğimiz grafiklerin yanında verimizin karakteristik özelliklerine bağlı olarak farklı gösterimleri de tercih edebiliriz:
- Zaman içindeki değişimleri göstermek için çizgi grafiklerini
- Parça ile bütün arasındaki ilişkiyi göstermek için pasta grafiklerini
- Konum verilerini görselleştirmek için harita grafiklerini
kullanabiliriz.
Sonuç
Keşifsel veri analizi, “makine öğrenmesi”10 ya da “istatiksel modelleme”ye11 başlanılmadan önce uygun model geliştirme ve sonuçları doğru bir şekilde yorumlama ihtiyacını karşılaması yönüyle kritik bir aşamadır. Veri bilimcisi için elde edilen sonuçların geçerliliğini doğrulaması, sonuçları düzgün şekilde göstermesi ve çalışılan iş üzerinde uygulanabilir kılması bakımından da önemlidir.
Çeviri Kaynağı: https://chartio.com/learn/data-analytics/what-is-exploratory-data-analysis/
2 Süsen veri seti (iris dataset), 1936 yılında İngiliz istatistikçi ve biyolog Ronald Fisher’ın süsen çiçeklerini sınıflandırması sonrası oluşturduğu çok değişkenli veri kümesi. Örnek çalışmalarda istatistikçiler tarafından kullanılmaktadır.
3 çok renkli süsen, virginya süseni, setosa süseni
4 çanak uzunluğu, çanak genişliği, taç uzunluğu, taç genişliği
5 birim, veri birimi, data point… (Temel Kavramlar bölümünde detaylı anlatılacaktır.)
6 aykırı değer (outlier)
7 Veri Türleri bölümünde kategorik verilere (categorical data) değinilecektir.
8 kümeleme analizi (cluster analysis)
9 istatistiksel sınıflandırma (statistical classification)
10 makine öğrenmesi (machine learning)
11 istatiksel modelleme (statistical modeling)